The GLMSELECT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics
Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Model selection from a very large number of effects is computationally demanding. For example, in analyzing microarray data (where each dot in the array corresponds to a regressor), it is not uncommon to have 35,000 such regressors. Large regression problems also arise when you want to consider all possible interactions of your main effects as candidates for inclusion in a selected model. For an example that uses this approach to build a predictive model for bankruptcy, see Foster and Stine (2004).
In recent years, there has been a resurgence of interest in combining variable selection methods with a screening approach that reduces the large number of regressors to a much smaller subset from which the model selection is performed. There are two categories of screening methods:
-
safe screening methods, by which the resulting solution is exactly the same as the solution when no screening is performed
-
heuristic screening methods, by which the resulting solution is not necessarily the same as the solution when no screening is performed
The heuristic screening approaches are usually much faster than the safe screening methods, but they are not guaranteed to reproduce the true LASSO or elastic net solution.
The safe screening approaches are developed mainly for the LASSO method and its extensions, which solve a well-defined convex optimization problem. For these methods, safe screening works as follows:
-
Given a solution
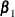 that corresponds to a regularization parameter
that corresponds to a regularization parameter 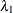 , safe screening approaches aim to identify the effects that are guaranteed to have zero coefficients in the solution
, safe screening approaches aim to identify the effects that are guaranteed to have zero coefficients in the solution 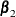 , which corresponds to the regularization parameter
, which corresponds to the regularization parameter 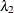 (
(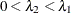 ).
).
-
The computation of
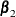 can exclude such inactive effects, thus saving computation cost.
can exclude such inactive effects, thus saving computation cost.
The idea of safe screening was pioneered by El Ghaoui, Viallon, and Rabbani (2012), and improved subsequently by other researchers (Liu et al., 2014; Wang et al., 2013; Xiang, Xu, and Ramadge, 2011).
If you specify SCREEN=SASVI in the model statement, PROC GLMSELECT uses the SASVI technique of Liu et al. (2014) to speed up LAR-type LASSO. The computation cost can usually be reduced while the solution is the same when you specify SCREEN=NONE.
Heuristic screening approaches (Fan and Lv, 2008; Tibshirani et al., 2012) use a screening statistic that is inexpensive to compute in order to eliminate regressors that are unlikely to be selected. For linear regression, you can use the magnitude of the correlation between each individual regressor and the response as such a screening statistic. The square of the correlation between a regressor and the response is the R-square value for the univariate regression of the response on this regressor. Hence, screening by the magnitude of the pairwise correlations is equivalent to fitting univariate models to do the screening.
The SIS (sure independence screening) approach proposed by Fan and Lv (2008) is a well-known heuristic screening approach that applies to model selection methods such as forward selection, backward selection, LASSO, and so on. When you specify SCREEN=SIS in the MODEL statement, PROC GLMSELECT first chooses only the subset of regressors whose screening statistics are among a specified number or percentage of the largest screening statistic values. When you specify SCREEN=SIS, PROC GLMSELECT uses the screening statistic that is the magnitude of the correlation between each individual regressor and the response. Then it performs model selection for the response from this screened subset of the original regressors.