The GLMPOWER Procedure
If the MODEL statement includes more than one dependent variable, you can indicate a multivariate model and define transformations of dependent variables by using the REPEATED statement.
The REPEATED
statement enables you to define custom Type III hypothesis tests by choosing from among several transformations of the dependent
variables: contrast, Helmert, identity, mean, polynomial, and profile. You can specify a transformation for each repeated
factor (often called a within-subject factor), and each combination of repeated factors produces an ![]() vector or matrix for testing the hypothesis
vector or matrix for testing the hypothesis ![]() . The
. The ![]() matrix consists of one or more between-subject contrasts that involve the model effects, and the
matrix consists of one or more between-subject contrasts that involve the model effects, and the ![]() matrix consists of one or more within-subject contrasts that involve the repeated factors. There is no limit to the number
of repeated factors that you can specify.
matrix consists of one or more within-subject contrasts that involve the repeated factors. There is no limit to the number
of repeated factors that you can specify.
Usually, the variables on the left side of the equation in the MODEL
statement represent one repeated response variable. This does not mean that you are limited to listing only one factor in
the REPEATED statement. For example, one repeated response variable (wellness rating) might be measured six times (implying
variables Y1 to Y6 on the left side of the equal sign in the MODEL
statement), with the associated within-subject factors rater and time (implying two factors listed in the REPEATED statement).
However, designs that have two or more repeated response variables can be handled by using the IDENTITY transformation
.
To use this feature, you must be familiar with the details of multivariate model and contrast parameterizations that PROC GLM uses. For more information, see the sections Repeated Measures Analysis of Variance and Multivariate Analysis of Variance in Chapter 45: The GLM Procedure. For information about the power and sample size computational methods and formulas, see the section Contrasts in Fixed-Effect Multivariate Models.
If you specify one or more REPEATED statements, then a "Mean(Dep)" transformation is added to the power analysis. This transformation is the mean of the dependent variables, the same transformation that is used implicitly in the "Tests of Hypotheses for Between Subjects Effects" table in PROC GLM. In addition, the Intercept model effect is included in the power analysis. If the REPEATED statement is not specified, then tests that involve the Intercept are excluded from the power analysis.
You can use either the REPEATED statement or the MANOVA statement along with any of the tests for multivariate models that are supported in the MTEST= option in the POWER statement. The REPEATED statement is usually used for handling repeated measurements on the same experimental unit, but you can also use the REPEATED statement for other situations, such as clusters or multiple outcome variables. The differences between the REPEATED and MANOVA statements are as follows:
-
You can use the REPEATED statement to specify commonly used contrasts by using keywords rather than coefficients, but you are limited to only those forms of the
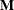 matrix.
matrix.
-
You can use the MANOVA statement to construct any
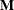 matrix, but you must specify the coefficients explicitly (except for the default identity matrix).
matrix, but you must specify the coefficients explicitly (except for the default identity matrix).
There is no limit to the number of REPEATED statements that you can specify. Each power analysis includes tests for all REPEATED statements and also (if you specify at least one REPEATED statement) the extra "Mean(Dep)" transformation that was previously mentioned.
The simplest form of the REPEATED statement requires only a factor-name. When you have two or more repeated factors, you must specify the factor-name and number of levels (levels) for each factor. Optionally, you can specify the actual values for the levels (level-values) and a transformation that defines single-degree-of-freedom contrasts. When you specify more than one within-subject factor, the factor-names (and associated level and transformation information) must be separated by a comma in the REPEATED statement.
The factor-specification for the REPEATED statement can include any number of individual factor specifications, separated by commas, of the following form:
factor-name levels < (level-values)> <transformation>
- factor-name
-
names a factor to be associated with the dependent variables. The name should not be the same as any variable name that already exists in the data set being analyzed and should conform to the usual conventions of SAS variable names.
When you specify more than one factor, list the dependent variables in the MODEL statement so that the within-subject factors that you define in the REPEATED statement are nested; that is, the first factor you define in the REPEATED statement should be the one whose values change least frequently.
- levels
-
gives the number of levels associated with the factor being defined. When there is only one within-subject factor, the number of levels is equal to the number of dependent variables. In this case, levels is optional. When more than one within-subject factor is defined, however, levels is required, and the product of the number of levels of all the factors must equal the number of dependent variables in the MODEL statement.
- (level-values)
-
gives values that correspond to levels of a repeated measures factor. These values are used as spacings for constructing orthogonal polynomial contrasts if you specify a POLYNOMIAL transformation. The number of values that you specify must correspond to the number of levels for that factor in the REPEATED statement. Enclose the level-values in parentheses.
The following transformation keywords define single-degree-of-freedom contrasts for factors that you specify in the REPEATED statement. Because the number of contrasts that are generated is always one less than the number of levels of the factor, you have some control over which contrast is omitted from the analysis by which transformation you select. The only exception is the IDENTITY transformation, which is not composed of contrasts and has the same degrees of freedom as the factor has levels. By default, PROC GLMPOWER uses the CONTRAST transformation.
When you specify more than one factor, list the dependent variables in the MODEL statement so that the within-subject factors that you define in the REPEATED statement are nested; that is, the first factor you define in the REPEATED statement should be the one whose values change least frequently. For example, assume that two raters submit a wellness rating at each of three times, for a total of six dependent variables for each subject. Consider the following statements:
proc glm; class treatment; model Y1-Y6 = treatment; repeated rater 2, time 3; run;
The variables are listed in the MODEL
statement as Y1 through Y6, so the REPEATED statement in the preceding statements implies the following structure:
|
Dependent Variables |
||||||
|
|
|
|
|
|
|
|
|
Value of |
1 |
1 |
1 |
2 |
2 |
2 |
|
Value of |
1 |
2 |
3 |
1 |
2 |
3 |
