The GLMPOWER Procedure

References

  • Castelloe, J. M. (2000), “Sample Size Computations and Power Analysis with the SAS System,” in Proceedings of the Twenty-Fifth Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.

  • Castelloe, J. M. and O’Brien, R. G. (2001), “Power and Sample Size Determination for Linear Models,” in Proceedings of the Twenty-Sixth Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.

  • Chi, Y.-Y., Gribbin, M. J., Lamers, Y., Gregory, J. F., III, and Muller, K. E. (2012), “Global Hypothesis Testing for High-Dimensional Repeated Measures Outcomes,” Statistics in Medicine, 31, 724–742.

  • Guo, Y., Logan, H. L., Glueck, D. H., and Muller, K. E. (2013), “Selecting a Sample Size for Studies with Repeated Measures,” BMC Medical Research Methodology, 13.

  • Hocking, R. R. (1985), The Analysis of Linear Models, Monterey, CA: Brooks/Cole.

  • Huynh, H. and Feldt, L. S. (1976), “Estimation of the Box Correction for Degrees of Freedom from Sample Data in the Randomized Block and Split Plot Designs,” Journal of Educational Statistics, 1, 69–82.

  • Lecoutre, B. (1991), “A Correction for the Epsilon Approximate Test with Repeated Measures Design with Two or More Independent Groups,” Journal of Educational Statistics, 16, 371–372.

  • Lenth, R. V. (2001), “Some Practical Guidelines for Effective Sample Size Determination,” American Statistician, 55, 187–193.

  • Logan, H. L., Baron, R. S., and Kohout, F. (1995), “Sensory Focus as Therapeutic Treatments for Acute Pain,” Psychosomatic Medicine, 57, 475–484.

  • McKeon, J. J. (1974), “F Approximations to the Distribution of Hotelling’s 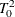$T_0^2$,” Biometrika, 61, 381–383.

  • Muller, K. E. and Barton, C. N. (1989), “Approximate Power for Repeated-Measures ANOVA Lacking Sphericity,” Journal of the American Statistical Association, 84, 549–555, also see "Correction to Approximate Power for Repeated-Measures ANOVA Lacking Sphericity," Journal of the American Statistical Association (1991), 86:255–256.

  • Muller, K. E. and Benignus, V. A. (1992), “Increasing Scientific Power with Statistical Power,” Neurotoxicology and Teratology, 14, 211–219.

  • Muller, K. E., Edwards, L. J., Simpson, S. L., and Taylor, D. J. (2007), “Statistical Tests with Accurate Size and Power for Balanced Linear Mixed Models,” Statistics in Medicine, 26, 3639–3660.

  • Muller, K. E. and Peterson, B. L. (1984), “Practical Methods for Computing Power in Testing the Multivariate General Linear Hypothesis,” Computational Statistics and Data Analysis, 2, 143–158.

  • O’Brien, R. G. and Castelloe, J. M. (2007), “Sample-Size Analysis for Traditional Hypothesis Testing: Concepts and Issues,” in A. Dmitrienko, C. Chuang-Stein, and R. D’Agostino, eds., Pharmaceutical Statistics Using SAS: A Practical Guide, 237–271, Cary, NC: SAS Institute Inc.

  • O’Brien, R. G. and Muller, K. E. (1993), “Unified Power Analysis for t-Tests through Multivariate Hypotheses,” in L. K. Edwards, ed., Applied Analysis of Variance in Behavioral Science, 297–344, New York: Marcel Dekker.

  • O’Brien, R. G. and Shieh, G. (1992), “Pragmatic, Unifying Algorithm Gives Power Probabilities for Common F Tests of the Multivariate General Linear Hypothesis,” Poster presented at the American Statistical Association Meetings, Boston, Statistical Computing Section.

  • Pillai, K. C. S. and Samson, P., Jr. (1959), “On Hotelling’s Generalization of 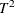$T^2$,” Biometrika, 46, 160–168.

  • Simpson, S. L., Edwards, L. J., Muller, K. E., Sen, P. K., and Styner, M. A. (2010), “A Linear Exponent AR(1) Family of Correlation Structures,” Statistics in Medicine, 29, 1825–1838.