The GEE Procedure (Experimental)
The following example demonstrates how you can fit a GEE model to count data. The data are analyzed by Diggle, Liang, and Zeger (1994). The response is the number of epileptic seizures, which was measured at the end of each of eight two-week treatment periods over sixteen weeks. The first eight weeks were the baseline period (during which no treatment was given), and the second eight weeks were the treatment period, during which patients received either a placebo or the drug progabide. The question of scientific interest is whether progabide is effective in reducing the rate of epileptic seizures.
The following DATA step creates the data set Seizure:
data Seizure; input ID Count Visit Trt Age Weeks; datalines; 104 11 0 0 31 8 104 5 1 0 31 2 104 3 2 0 31 2 104 3 3 0 31 2 104 3 4 0 31 2 106 11 0 0 30 8 ... more lines ... 236 12 0 1 37 8 236 1 1 1 37 2 236 4 2 1 37 2 236 3 3 1 37 2 236 2 4 1 37 2 ;
The following DATA step creates a log time interval variable for use as an offset and an indicator variable for whether the observation is for a baseline measurement or a visit measurement. Patient 207 is deleted as an outlier, which was done in the Diggle et al. (2002) analysis:
data Seizure;
set Seizure;
if ID ne 207;
if Visit = 0 then do;
X1=0;
Ltime = log(8);
end;
else do;
X1=1;
Ltime=log(2);
end;
run;
Poisson regression is commonly used to model count data. In this example, the log-linear Poisson model is specified by ![]() (the Poisson variance function) and a log link function,
(the Poisson variance function) and a log link function,
where
-
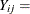 number of epileptic seizures in interval j
number of epileptic seizures in interval j
-
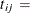 length of interval j
length of interval j
-
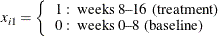
-
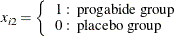
Because the visits represent repeated measurements, the responses from the same individual are correlated and inferences need
to take this into account. The correlations between the counts are modeled as ![]() ,
, ![]() (exchangeable correlations).
(exchangeable correlations).
In this model, the regression parameters are interpreted in terms of the log seizure rate that is displayed in Table 42.11.
Table 42.11: Interpretation of Regression Parameters
|
Treatment |
Visit |
|
|---|---|---|
|
Placebo |
Baseline |
|
|
1–4 |
|
|
|
Progabide |
Baseline |
|
|
1–4 |
|
The difference between the log seizure rates in the pretreatment (baseline) period and the treatment periods is ![]() for the placebo group and
for the placebo group and ![]() for the progabide group. A value of
for the progabide group. A value of ![]() indicates a reduction in the seizure rate.
indicates a reduction in the seizure rate.
The following statements perform the analysis:
proc gee data = Seizure; class ID Visit; model Count = X1 Trt X1*Trt / dist=poisson link=log offset= Ltime; repeated subject = ID / within = Visit type=unstr covb corrw; run;
In the MODEL statement, Count is the response variable, and X1, Trt, and the interaction X1*Trt are the explanatory variables. You request Poisson regression with the DIST=POISSON and the LINK=LOG options. The offset
variable is often used in Poisson regression to account for different exposures. In this case, the OFFSET= option specifies
Ltime as the offset variable representing different time intervals.
In the REPEATED statement, the SUBJECT= option indicates that the variable ID identifies the observations from a single cluster, and the TYPE=UNSTR option specifies the unstructured working correlation
structure. The CORRW option requests that the working correlation matrix be displayed.
The "Model Information" table that is displayed in Output 42.2.1 provides information about the specified model and the input data set.
Output 42.2.2 displays general information about the GEE model analysis.
Output 42.2.3 displays the parameter estimate covariance matrices, which are requested by the COVB option. Both model-based and empirical covariances are produced.
The exchangeable working correlation matrix is displayed in Output 42.2.4. It shows that there are noticeable correlations among the respective visits.
The parameter estimates table, shown in Output 42.2.5, contains parameter estimates, standard errors, confidence intervals, Z scores, and p-values for the parameter estimates. Empirical standard error estimates are used in this table.
Output 42.2.5: Parameter Estimates Table
| Parameter Estimates for Response Model | ||||||
|---|---|---|---|---|---|---|
| with Empirical Standard Error | ||||||
| Parameter | Estimate | Standard Error |
95% Confidence Limits | Z | Pr > |Z| | |
| Intercept | 1.3309 | 0.1612 | 1.0151 | 1.6468 | 8.26 | <.0001 |
| X1 | 0.1128 | 0.0927 | -0.0689 | 0.2945 | 1.22 | 0.2237 |
| Trt | -0.1034 | 0.1960 | -0.4875 | 0.2807 | -0.53 | 0.5978 |
| X1*Trt | -0.3162 | 0.1496 | -0.6093 | -0.0231 | -2.11 | 0.0345 |
The estimate of ![]() is –0.3162, which indicates that progabide is effective in reducing the rate of epileptic seizures.
is –0.3162, which indicates that progabide is effective in reducing the rate of epileptic seizures.
Model fit criteria for the model are displayed in Output 42.2.6. These criteria are used in selecting selecting regression models and working correlations.
