The GEE Procedure (Experimental)
In longitudinal studies, response measurements are often missing because of skipped visits or dropouts. Suppose ![]() is the indicator that the response
is the indicator that the response ![]() is observed, where
is observed, where ![]() if
if ![]() is observed and 0 otherwise. Missing data patterns can be classified into two types: dropout and intermittent. A dropout
occurs if an individual skips a particular visit and then never comes back for subsequent visits. That is, if
is observed and 0 otherwise. Missing data patterns can be classified into two types: dropout and intermittent. A dropout
occurs if an individual skips a particular visit and then never comes back for subsequent visits. That is, if ![]() , then
, then ![]() for all
for all ![]() . Otherwise, the missing data pattern is intermittent. Intermittent patterns can be quite complicated; only dropout patterns
are considered here.
. Otherwise, the missing data pattern is intermittent. Intermittent patterns can be quite complicated; only dropout patterns
are considered here.
The mechanism for missingness can be described by a statistical model for the probability of observing a missing value, and making the right assumption about the mechanism is crucial to methods that handle missing data. Missingness mechanisms are classified into three types: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR) (Rubin, 1976).
Assumptions about longitudinal data that include missing responses caused by dropouts are classified as follows:
-
The data are said to be MCAR if the probability of a missing response is independent of its past, current, and future responses conditional on the covariates. That is,
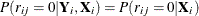 .
.
-
The data are said to be MAR if the probability of a missing response is independent of its current and future responses conditional on the observed past responses and the covariates. That is,
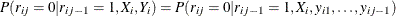 . MAR is a weaker assumption than MCAR.
. MAR is a weaker assumption than MCAR.
-
The data are said to be MNAR if the probability of a missing response depends on the unobserved responses. MNAR is the most general and the most problematic missing-data scenario.
The GEE procedure implements two different weighted methods (observation-specific and subject-specific) for estimating the
regression parameter ![]() when dropouts occur. Both provide consistent estimates if the data are MAR.
when dropouts occur. Both provide consistent estimates if the data are MAR.
Suppose ![]() is the weight for
is the weight for ![]() , which is defined as the inverse probability of observing
, which is defined as the inverse probability of observing ![]() . In other words,
. In other words, ![]() . Suppose
. Suppose ![]() is a
is a ![]() diagonal matrix whose jth diagonal is
diagonal matrix whose jth diagonal is ![]() . The responses for the ith subject are
. The responses for the ith subject are ![]() . Consider the following weighted generalized estimating equations (Robins and Rotnitzky, 1995; Preisser, Lohman, and Rathouz, 2002):
. Consider the following weighted generalized estimating equations (Robins and Rotnitzky, 1995; Preisser, Lohman, and Rathouz, 2002):
Unlike the standard generalized estimating equations, the weighted generalized estimating equations are unbiased when the
observations are appropriately weighted and lead to consistent estimates of ![]() .
.
The weights ![]() are often unknown in practice and are estimated by a logistic regression model under the MAR assumption. Specifically, say
that
are often unknown in practice and are estimated by a logistic regression model under the MAR assumption. Specifically, say
that ![]() denotes the probability of observing the response
denotes the probability of observing the response ![]() given its observed previous responses.
given its observed previous responses.
Under the MAR assumption,
Using the observed data, ![]() can be predicted from a logistic regression model,
can be predicted from a logistic regression model,
where the ![]() are predictors that usually include the covariates
are predictors that usually include the covariates ![]() , the past responses, and the indicators for visit times. The dropout process implies that the estimated probability of observing
, the past responses, and the indicators for visit times. The dropout process implies that the estimated probability of observing
![]() can be expressed as a cumulative product of conditional probabilities:
can be expressed as a cumulative product of conditional probabilities:
With the estimated weights ![]() , the regression parameter
, the regression parameter ![]() is estimated by solving the equation for
is estimated by solving the equation for ![]() .
.
The regression parameter ![]() can be estimated by solving for
can be estimated by solving for ![]() after plugging in the estimated weights. The fitting algorithm is described in the section Fitting Algorithm for Weighted GEE.
after plugging in the estimated weights. The fitting algorithm is described in the section Fitting Algorithm for Weighted GEE.
Unlike the observation-specific weighted method, which assigns an observation-specific weight to each observation, the subject-specific weighted method assigns a single weight to each subject. In other words, all the observations from a subject receive the same weight. Specifically, the subject-specific weighted method obtains the regression parameter estimates by solving the equations
where the responses for the ith subject are ![]() and the weight
and the weight ![]() for subject i is the inverse probability of a subject i dropping out at the observed time (Fitzmaurice, Molenberghs, and Lipsitz, 1995; Preisser, Lohman, and Rathouz, 2002). Note that the weight
for subject i is the inverse probability of a subject i dropping out at the observed time (Fitzmaurice, Molenberghs, and Lipsitz, 1995; Preisser, Lohman, and Rathouz, 2002). Note that the weight ![]() is a scalar, in contrast to the weight matrix
is a scalar, in contrast to the weight matrix ![]() that the observation-specific weighted GEE method uses.
that the observation-specific weighted GEE method uses.
The subject-specific weighted estimating equations are also unbiased when the subjects are appropriately weighted and lead
to consistent estimates of the regression parameters ![]() .
.
The weight ![]() is usually unknown in practice and needs to be estimated. Suppose subject i drops out at time
is usually unknown in practice and needs to be estimated. Suppose subject i drops out at time ![]() . Assume that the first visit
. Assume that the first visit ![]() is always observed with
is always observed with ![]() . Thus, the dropout times
. Thus, the dropout times ![]() range from 2 to T+1. Note that a dropout time of T+1 indicates that subject i completes all the
range from 2 to T+1. Note that a dropout time of T+1 indicates that subject i completes all the ![]() visits and dropout does not occur.
visits and dropout does not occur.
The weight ![]() is defined as follows: if subject i drops out before completing the last visit (that is,
is defined as follows: if subject i drops out before completing the last visit (that is, ![]() ), then
), then ![]() ; otherwise, the subject completes all the
; otherwise, the subject completes all the ![]() visits (that is,
visits (that is, ![]() ), and
), and ![]() .
.
Similar to the process for the observation-specific weighted method, the dropout process for the subject-specific weighted method implies that subject-specific weights can be estimated as a cumulative product of conditional probabilities:
Thus, the subject-specific weights ![]() can be obtained after
can be obtained after ![]() is estimated by fitting a logistic regression to the data
is estimated by fitting a logistic regression to the data ![]() .
.
The regression parameter ![]() from the subject-specific weighted GEE method can be estimated by solving for
from the subject-specific weighted GEE method can be estimated by solving for ![]() after plugging in the estimated weights. The fitting algorithm is described in the section Fitting Algorithm for Weighted GEE. The subject-specific weighting scheme was originally developed for computational convenience. Preisser, Lohman, and Rathouz
(2002) showed that the observation-level weighted GEE method produces more efficient estimates than the cluster-level weighted
GEE method for incomplete longitudinal binary data.
after plugging in the estimated weights. The fitting algorithm is described in the section Fitting Algorithm for Weighted GEE. The subject-specific weighting scheme was originally developed for computational convenience. Preisser, Lohman, and Rathouz
(2002) showed that the observation-level weighted GEE method produces more efficient estimates than the cluster-level weighted
GEE method for incomplete longitudinal binary data.
The following fitting algorithm fits marginal models by using the observation-specific or the subject-specific weighted GEE method when the dropout process is missing at random:
-
Fit a logistic regression to the data
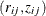 to obtain an estimate of
to obtain an estimate of  and estimate the weights.
and estimate the weights.
-
Compute an initial estimate of
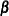 by using an ordinary generalized linear model, assuming independence of the responses.
by using an ordinary generalized linear model, assuming independence of the responses.
-
Compute the working correlation matrix
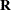 based on the standardized residuals, the current estimate of
based on the standardized residuals, the current estimate of 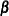 , and the specified structure of
, and the specified structure of 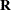 .
.
-
Compute the estimated covariance matrix:
![\[ \mb{V}_{i} = \phi \mb{A}_ i^{\frac{1}{2}} \hat{\mb{R}}(\balpha ) \mb{A}_ i^{\frac{1}{2}} \]](images/statug_gee0112.png)
-
Update
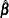 :
:
![\[ \hat\bbeta _{r+1} = \hat\bbeta _{r} + \left[\sum _{i=1}^{K} \frac{\partial \bmu _ i}{\partial \bbeta }^{\prime } \mb{V}_{i}^{-1} \frac{\partial \bmu _ i}{\partial \bbeta } \right]^{-1} \left[ \sum _{i=1}^ K \frac{\partial \bmu _ i}{\partial \bbeta }^{\prime }\mb{V}_{i}^{-1} \mb{W}_ i (\mb{Y}_{i}-\bmu _ i) \right] \]](images/statug_gee0114.png)
where
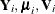 , and
, and 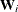 are as follows:
are as follows:
-
For the observation-specific weighted method,
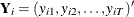 ;
; 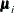 and
and 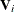 are its corresponding mean vector and working covariance matrix, respectively; and
are its corresponding mean vector and working covariance matrix, respectively; and 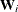 is a
is a 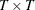 diagonal matrix whose jth diagonal is
diagonal matrix whose jth diagonal is 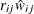 .
.
-
For the subject-specific weighted method,
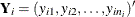 ;
; 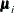 and
and 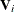 are its corresponding mean vector and working covariance matrix, respectively; and
are its corresponding mean vector and working covariance matrix, respectively; and 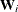 is a
is a 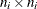 diagonal matrix whose jth diagonal is
diagonal matrix whose jth diagonal is 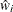 .
.
-
-
Repeat steps 3–5 until convergence.
Note that you can use the WEIGHT statement in the GENMOD procedure to perform a two-stage strategy that is often used in practice
to obtain the weighted GEE estimates. You fit a logistic regression to the data ![]() to obtain the weights as described in the preceding steps. Then you estimate
to obtain the weights as described in the preceding steps. Then you estimate ![]() by specifying the estimated weights in the WEIGHT statement in PROC GENMOD for the GEE analysis. For the subject-specific
weighted GEE method, this approach is appropriate for any working correlation structure. However, for the observation-specific
weighted method, this approach is appropriate only for the independent working correlation structure.
by specifying the estimated weights in the WEIGHT statement in PROC GENMOD for the GEE analysis. For the subject-specific
weighted GEE method, this approach is appropriate for any working correlation structure. However, for the observation-specific
weighted method, this approach is appropriate only for the independent working correlation structure.
The two-stage approach results in standard errors that are larger than those that are produced by using the MISSMODEL statement in the GEE procedure (because PROC GENMOD treats the weights as fixed and known). Thus, the two-stage approach that uses PROC GENMOD results in conservative inference (Fitzmaurice, Laird, and Ware, 2011). The GEE procedure computes the parameter estimate covariances as described in (Fitzmaurice, Laird, and Ware, 2011) and Preisser, Lohman, and Rathouz (2002).
Suppose that each subject in a longitudinal study is measured at T times. In other words, for the ith subject you measure T responses ![]() and T corresponding covariates
and T corresponding covariates ![]() .
.
By default, the GEE procedure handles missing data in the same manner as the standard GEE method in the GENMOD procedure. The working correlation matrix is estimated from data that contain both intermittent and dropout types of missing values by using the all-available-pairs method, in which all nonmissing pairs of data are used in the moment estimators. The resulting covariances and standard errors are valid under the missing completely at random (MCAR) assumption. For more information, see the section Missing Data in Chapter 43: The GENMOD Procedure.
When you specify the MISSMODEL statement in the GEE procedure to use the weighted GEE method to analyze the data, the procedure uses observations that have missing values in the response, provided that the missing values for all subjects are caused by dropouts. If the missing values are intermittent for any of the subjects, then the weighted GEE method does not apply and the procedure terminates.
For the observation-specific weighted GEE method, the covariates for all the observations for a subject must be observed, regardless of whether the response is missing. For each subject, the input data set must provide T observations.
For the subject-specific weighted GEE method, the covariates for a subject who drops out at time k must be observed for the observations up to and including time k. The input data set must provide at least k observations for this subject. The covariates must be observed for all observations on a subject who completes the study, and the input data set must provide T observations for this subject.
For more information about how weighted GEE methods handle missing values, see Fitzmaurice, Laird, and Ware (2011) and Preisser, Lohman, and Rathouz (2002).
