The MIXED Procedure
REPEATED <repeated-effect> </ options> ;
The REPEATED statement is used to specify the ![]() matrix in the mixed model. Its syntax is different from that of the REPEATED statement in PROC GLM. If no REPEATED statement
is specified,
matrix in the mixed model. Its syntax is different from that of the REPEATED statement in PROC GLM. If no REPEATED statement
is specified, ![]() is assumed to be equal to
is assumed to be equal to ![]() .
.
For many repeated measures models, no repeated effect is required in the REPEATED statement. Simply use the SUBJECT= option to define the blocks of ![]() and the TYPE= option to define their covariance structure. In this case, the repeated measures data must be similarly ordered for each
subject, and you must indicate all missing response variables with periods in the input data set unless they all fall at the
end of a subject’s repeated response profile. These requirements are necessary in order to inform PROC MIXED of the proper
location of the observed repeated responses.
and the TYPE= option to define their covariance structure. In this case, the repeated measures data must be similarly ordered for each
subject, and you must indicate all missing response variables with periods in the input data set unless they all fall at the
end of a subject’s repeated response profile. These requirements are necessary in order to inform PROC MIXED of the proper
location of the observed repeated responses.
Specifying a repeated effect is useful when you do not want to indicate missing values with periods in the input data set.
The repeated effect must contain only classification variables. Make sure that the levels of the repeated effect are different
for each observation within a subject; otherwise, PROC MIXED constructs identical rows in ![]() corresponding to the observations with the same level. This results in a singular
corresponding to the observations with the same level. This results in a singular ![]() and an infinite likelihood.
and an infinite likelihood.
Whether you specify a REPEATED effect or not, the rows of ![]() for each subject are constructed in the order in which they appear in the input data set.
for each subject are constructed in the order in which they appear in the input data set.
Table 63.16 summarizes the options available in the REPEATED statement. All options are subsequently discussed in alphabetical order.
Table 63.16: Summary of REPEATED Statement Options
|
Option |
Description |
|---|---|
|
Construction of Covariance Structure |
|
|
Defines an effect specifying heterogeneity in the R-side covariance structure |
|
|
Specifies data set with coefficient matrices for TYPE=LIN |
|
|
Requests that a diagonal matrix be added to |
|
|
Specifies that only the local effects are weighted |
|
|
Specifies that only the nonlocal effects are weighted |
|
|
Identifies the subjects in the R-side model |
|
|
Specifies the R-side covariance structure |
|
|
Statistical Output |
|
|
Produces a table of Hotelling-Lawley-McKeon statistics (McKeon, 1974) |
|
|
Produces a table of Hotelling-Lawley-Pillai-Samson statistics (Pillai and Samson, 1959) |
|
|
Displays blocks of the estimated |
|
|
Display the Cholesky root (lower) of blocks of the estimated |
|
|
Displays the inverse Cholesky root (lower) of blocks of the estimated |
|
|
Displays the correlation matrix corresponding to blocks of the estimated |
|
|
Displays the inverse of blocks of the estimated |
|
You can specify the following options in the REPEATED statement after a slash (/).
-
GROUP=effect
GRP=effect -
defines an effect that specifies heterogeneity in the covariance structure of
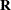 . All observations that have the same level of the GROUP effect have the same covariance parameters. Each new level of the
GROUP effect produces a new set of covariance parameters with the same structure as the original group. You should exercise
caution in properly defining the GROUP effect, because strange covariance patterns can result with its misuse. Also, the GROUP
effect can greatly increase the number of estimated covariance parameters, which can adversely affect the optimization process.
. All observations that have the same level of the GROUP effect have the same covariance parameters. Each new level of the
GROUP effect produces a new set of covariance parameters with the same structure as the original group. You should exercise
caution in properly defining the GROUP effect, because strange covariance patterns can result with its misuse. Also, the GROUP
effect can greatly increase the number of estimated covariance parameters, which can adversely affect the optimization process.
Continuous variables are permitted as arguments to the GROUP= option. PROC MIXED does not sort by the values of the continuous variable; rather, it considers the data to be from a new subject or group whenever the value of the continuous variable changes from the previous observation. Using a continuous variable decreases execution time for models with a large number of subjects or groups and also prevents the production of a large “Class Level Information” table.
- HLM
-
produces a table of Hotelling-Lawley-McKeon statistics (McKeon, 1974) for all fixed effects whose levels change across data having the same level of the SUBJECT= effect (the within-subject fixed effects). This option applies only when you specify a REPEATED statement with the TYPE=UN option and no RANDOM statements. For balanced data, this model is equivalent to the multivariate model for repeated measures in PROC GLM.
The Hotelling-Lawley-McKeon statistic has a slightly better F approximation than the Hotelling-Lawley-Pillai-Samson statistic (see the description of the HLPS option, which follows). Both of the Hotelling-Lawley statistics can perform much better in small samples than the default F statistic (Wright, 1994).
Separate tables are produced for Type 1, 2, and 3 tests, according to the ones you select. The ODS table names are HLM1, HLM2, and HLM3, respectively.
- HLPS
-
produces a table of Hotelling-Lawley-Pillai-Samson statistics (Pillai and Samson, 1959) for all fixed effects whose levels change across data having the same level of the SUBJECT= effect (the within-subject fixed effects). This option applies only when you specify a REPEATED statement with the TYPE=UN option and no RANDOM statements. For balanced data, this model is equivalent to the multivariate model for repeated measures in PROC GLM, and this statistic is the same as the Hotelling-Lawley Trace statistic produced by PROC GLM.
Separate tables are produced for Type 1, 2, and 3 tests, according to the ones you select. The ODS table names are HLPS1, HLPS2, and HLPS3, respectively.
- LDATA=SAS-data-set
-
reads the coefficient matrices associated with the TYPE=LIN(number) option. The data set must contain the variables
Parm,Row,Col1–Coln orParm,Row,Col,Value. TheParmvariable denotes which of the number coefficient matrices is currently being constructed, and theRow,Col1–Coln, orRow,Col,Valuevariables specify the matrix values, as they do with the RANDOM statement option GDATA=. Unspecified values of these matrices are set equal to 0. -
LOCAL
LOCAL=EXP(<effects>)
LOCAL=POM(POM-data-set) -
requests that a diagonal matrix be added to
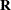 . With just the
LOCAL option, this diagonal matrix equals
. With just the
LOCAL option, this diagonal matrix equals 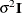 , and
, and 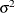 becomes an additional variance parameter that PROC MIXED profiles out of the likelihood provided that you do not specify
the NOPROFILE option in the PROC MIXED statement. The LOCAL option is useful if you want to add an observational error to a time series structure (Jones and Boadi-Boateng,
1991) or a nugget effect to a spatial structure Cressie (1993).
becomes an additional variance parameter that PROC MIXED profiles out of the likelihood provided that you do not specify
the NOPROFILE option in the PROC MIXED statement. The LOCAL option is useful if you want to add an observational error to a time series structure (Jones and Boadi-Boateng,
1991) or a nugget effect to a spatial structure Cressie (1993).
The LOCAL=EXP(<effects>) option produces exponential local effects, also known as dispersion effects, in a log-linear variance model. These local effects have the form
![\[ \sigma ^{2}\mr {diag} [\mr {exp} (\bU \bdelta )] \]](images/statug_mixed0168.png)
where
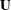 is the full-rank design matrix corresponding to the effects that you specify and
is the full-rank design matrix corresponding to the effects that you specify and 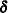 are the parameters that PROC MIXED estimates. An intercept is not included in
are the parameters that PROC MIXED estimates. An intercept is not included in 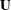 because it is accounted for by
because it is accounted for by 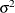 . PROC MIXED constructs the full-rank
. PROC MIXED constructs the full-rank 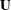 in terms of 1s and –1s for classification effects. Be sure to scale continuous effects in
in terms of 1s and –1s for classification effects. Be sure to scale continuous effects in 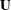 sensibly.
sensibly.
The LOCAL=POM(POM-data-set) option specifies the power-of-the-mean structure. This structure possesses a variance of the form
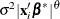 for the ith observation, where
for the ith observation, where 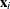 is the ith row of
is the ith row of 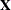 (the design matrix of the fixed effects) and
(the design matrix of the fixed effects) and 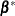 is an estimate of the fixed-effects parameters that you specify in POM-data-set.
is an estimate of the fixed-effects parameters that you specify in POM-data-set.
The SAS data set specified by POM-data-set contains the numeric variable
Estimate(in previous releases, the variable name was required to beEST), and it has at least as many observations as there are fixed-effects parameters. The first p observations of theEstimatevariable in POM-data-set are taken to be the elements of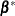 , where p is the number of columns of
, where p is the number of columns of 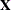 . You must order these observations according to the non-full-rank parameterization of the MIXED procedure. One easy way to
set up POM-data-set for a
. You must order these observations according to the non-full-rank parameterization of the MIXED procedure. One easy way to
set up POM-data-set for a 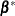 corresponding to ordinary least squares is illustrated by the following statements:
corresponding to ordinary least squares is illustrated by the following statements:
ods output SolutionF=sf; proc mixed; class a; model y = a x / s; run; proc mixed; class a; model y = a x; repeated / local=pom(sf); run;
Note that the generalized least squares estimate of the fixed-effects parameters from the second PROC MIXED step usually is not the same as your specified
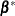 . However, you can iterate the POM fitting until the two estimates agree. Continuing from the previous example, the statements
for performing one step of this iteration are as follows:
. However, you can iterate the POM fitting until the two estimates agree. Continuing from the previous example, the statements
for performing one step of this iteration are as follows:
ods output SolutionF=sf1; proc mixed; class a; model y = a x / s; repeated / local=pom(sf); run; proc compare brief data=sf compare=sf1; var estimate; run; data sf; set sf1; run;
Unfortunately, this iterative process does not always converge. For further details, see the description of pseudo-likelihood in Chapter 3 of Carroll and Ruppert (1988).
- LOCALW
-
specifies that only the local effects and no others be weighted. By default, all effects are weighted. The LOCALW option is used in connection with the WEIGHT statement and the LOCAL option in the REPEATED statement.
- NONLOCALW
-
specifies that only the nonlocal effects and no others be weighted. By default, all effects are weighted. The NONLOCALW option is used in connection with the WEIGHT statement and the LOCAL option in the REPEATED statement.
- R<=value-list>
-
requests that blocks of the estimated
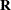 matrix be displayed.
The first block determined by the SUBJECT= effect is the default displayed block. PROC MIXED displays blanks for value-lists that are 0.
matrix be displayed.
The first block determined by the SUBJECT= effect is the default displayed block. PROC MIXED displays blanks for value-lists that are 0.
The value-list indicates the subjects for which blocks of
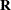 are to be displayed. For example, the following statement displays block matrices for the first, third, and fifth persons:
are to be displayed. For example, the following statement displays block matrices for the first, third, and fifth persons:
repeated / type=cs subject=person r=1,3,5;
See the PARMS statement for the possible forms of value-list. The ODS table name is R.
- RC<=value-list>
-
produces the Cholesky root of blocks of the estimated
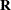 matrix. The value-list specification is the same as with the R option. The ODS table name is CholR.
matrix. The value-list specification is the same as with the R option. The ODS table name is CholR.
- RCI<=value-list>
-
produces the inverse Cholesky root of blocks of the estimated
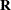 matrix. The value-list specification is the same as with the R option. The ODS table name is InvCholR.
matrix. The value-list specification is the same as with the R option. The ODS table name is InvCholR.
- RCORR<=value-list>
-
produces the correlation matrix corresponding to blocks of the estimated
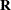 matrix. The value-list specification is the same as with the R option. The ODS table name is RCorr.
matrix. The value-list specification is the same as with the R option. The ODS table name is RCorr.
- RI<=value-list>
-
produces the inverse of blocks of the estimated
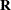 matrix.
The value-list specification is the same as with the R option. The ODS table name is InvR.
matrix.
The value-list specification is the same as with the R option. The ODS table name is InvR.
- SSCP
-
requests that an unstructured
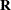 matrix be estimated from
the sum-of-squares-and-crossproducts matrix of the residuals. It applies only when you specify TYPE=UN and have no RANDOM statements. Also, you must have a sufficient number of subjects for the estimate to be positive definite.
matrix be estimated from
the sum-of-squares-and-crossproducts matrix of the residuals. It applies only when you specify TYPE=UN and have no RANDOM statements. Also, you must have a sufficient number of subjects for the estimate to be positive definite.
This option is useful when the size of the blocks of
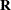 is large (for example, greater than 10) and you want to use or inspect an unstructured estimate that is much quicker to compute
than the default REML estimate. The two estimates will agree for certain balanced data sets when you have a classification
fixed effect defined across all time points within a subject.
is large (for example, greater than 10) and you want to use or inspect an unstructured estimate that is much quicker to compute
than the default REML estimate. The two estimates will agree for certain balanced data sets when you have a classification
fixed effect defined across all time points within a subject.
-
SUBJECT=effect
SUB=effect -
identifies the subjects in your mixed model. Complete independence is assumed across subjects; therefore, the SUBJECT= option produces a block-diagonal structure in
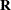 with identical blocks. When the SUBJECT= effect consists entirely of classification variables, the blocks of
with identical blocks. When the SUBJECT= effect consists entirely of classification variables, the blocks of 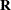 correspond to observations sharing the same level of that effect. These blocks are sorted according to this effect as well.
correspond to observations sharing the same level of that effect. These blocks are sorted according to this effect as well.
Continuous variables are permitted as arguments to the SUBJECT= option. PROC MIXED does not sort by the values of the continuous variable; rather, it considers the data to be from a new subject or group whenever the value of the continuous variable changes from the previous observation. Using a continuous variable decreases execution time for models with a large number of subjects or groups and also prevents the production of a large “Class Level Information” table.
If you want to model nonzero covariance among all of the observations in your SAS data set, specify SUBJECT=INTERCEPT to treat the data as if they are all from one subject. However, be aware that in this case PROC MIXED manipulates an
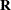 matrix with dimensions equal to the number of observations. If no SUBJECT= effect is specified, then every observation is
assumed to be from a different subject and
matrix with dimensions equal to the number of observations. If no SUBJECT= effect is specified, then every observation is
assumed to be from a different subject and 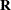 is assumed to be diagonal. For this reason, you usually want to use the SUBJECT= option in the REPEATED statement.
is assumed to be diagonal. For this reason, you usually want to use the SUBJECT= option in the REPEATED statement.
- TYPE=covariance-structure
-
specifies the covariance structure of the
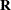 matrix. The
SUBJECT= option defines the blocks of
matrix. The
SUBJECT= option defines the blocks of 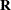 , and the TYPE= option specifies the structure of these blocks. Valid values for covariance-structure and their descriptions are provided in Table 63.17 and Table 63.18. The default structure is VC.
, and the TYPE= option specifies the structure of these blocks. Valid values for covariance-structure and their descriptions are provided in Table 63.17 and Table 63.18. The default structure is VC.
Table 63.17: Covariance Structures
Structure
Description
Parms
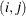 element
element
ANTE(1)
Antedependence
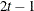
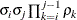
AR(1)
Autoregressive(1)
2
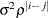
ARH(1)
Heterogeneous AR(1)
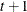
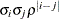
ARMA(1,1)
ARMA(1,1)
3
![$\sigma ^2[\gamma \rho ^{|i-j|-1} 1(i\neq j) + 1(i=j)]$](images/statug_mixed0181.png)
CS
Compound symmetry
2
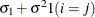
CSH
Heterogeneous CS
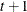
![$\sigma _{i}\sigma _{j}[\rho 1(i \neq j)+ 1(i=j)]$](images/statug_mixed0183.png)
FA(q)
Factor analytic
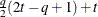
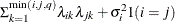
FA0(q)
No diagonal FA
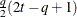
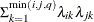
FA1(q)
Equal diagonal FA
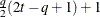
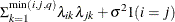
HF
Huynh-Feldt
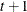
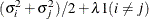
LIN(q)
General linear
q
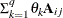
TOEP
Toeplitz
t
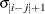
TOEP(q)
Banded Toeplitz
q
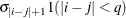
TOEPH
Heterogeneous TOEP
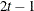
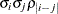
TOEPH(q)
Banded hetero TOEP
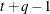
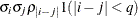
UN
Unstructured
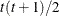
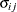
UN(q)
Banded
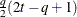
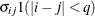
UNR
Unstructured corrs
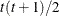
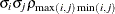
UNR(q)
Banded correlations
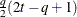
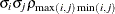
UN@AR(1)
Direct product AR(1)
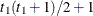
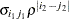
UN@CS
Direct product CS
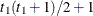
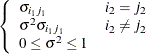
UN@UN
Direct product UN
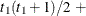
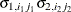
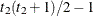
VC
Variance components
q
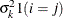
and i corresponds to kth effect
In Table 63.17, “Parms” is the number of covariance parameters in the structure, t is the overall dimension of the covariance matrix, and
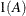 equals 1 when A is true and 0 otherwise. For example, 1
equals 1 when A is true and 0 otherwise. For example, 1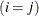 equals 1 when
equals 1 when 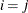 and 0 otherwise, and 1
and 0 otherwise, and 1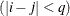 equals 1 when
equals 1 when 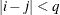 and 0 otherwise. For the TYPE=TOEPH structures,
and 0 otherwise. For the TYPE=TOEPH structures, 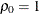 , and for the TYPE=UNR structures,
, and for the TYPE=UNR structures, 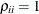 for all i. For the direct product structures, the subscripts “1” and “2” see the first and second structure in the direct product, respectively, and
for all i. For the direct product structures, the subscripts “1” and “2” see the first and second structure in the direct product, respectively, and 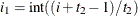 ,
, 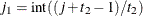 ,
, 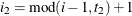 , and
, and 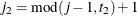 .
.
Table 63.18: Spatial Covariance Structures
Structure
Description
Parms
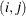 element
element
SP(EXP)(c-list )
Exponential
2
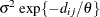
SP(EXPA)(c-list )
Anisotropic exponential
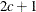
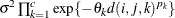
SP(EXPGA)(
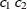 )
)
2D exponential,
4
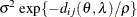
geometrically anisotropic
SP(GAU)(c-list )
Gaussian
2
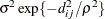
SP(GAUGA)(
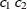 )
)
2D Gaussian,
4
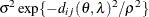
geometrically anisotropic
SP(LIN)(c-list )
Linear
2
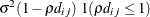
SP(LINL)(c-list )
Linear log
2
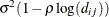
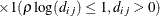
SP(MATERN)(c-list)
Matérn
3
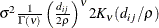
SP(MATHSW)(c-list)
Matérn
3
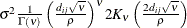
(Handcock-Stein-Wallis)
SP(POW)(c-list)
Power
2
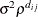
SP(POWA)(c-list)
Anisotropic power
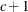
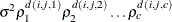
SP(SPH)(c-list )
Spherical
2
![$\sigma ^2[1 - (\frac{3d_{ij}}{2\rho }) + (\frac{d^3_{ij}}{2\rho ^3})]\ 1(d_{ij} \leq \rho )$](images/statug_mixed0235.png)
SP(SPHGA)(
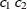 )
)
2D Spherical,
4
![$\sigma ^2[1 - (\frac{3d_{ij}(\theta ,\lambda )}{2\rho }) + (\frac{d_{ij}(\theta ,\lambda )^3}{2\rho ^3})]$](images/statug_mixed0236.png)
geometrically anisotropic
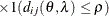
In Table 63.18, c-list contains the names of the numeric variables used as coordinates of the location of the observation in space, and
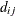 is the Euclidean distance between the ith and jth vectors of these coordinates, which correspond to the ith and jth observations in the input data set. For SP(POWA) and SP(EXPA), c is the number of coordinates, and
is the Euclidean distance between the ith and jth vectors of these coordinates, which correspond to the ith and jth observations in the input data set. For SP(POWA) and SP(EXPA), c is the number of coordinates, and 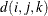 is the absolute distance between the kth coordinate,
is the absolute distance between the kth coordinate, 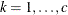 , of the ith and jth observations in the input data set. For the geometrically anisotropic structures SP(EXPGA), SP(GAUGA), and SP(SPHGA), exactly
two spatial coordinate variables must be specified as
, of the ith and jth observations in the input data set. For the geometrically anisotropic structures SP(EXPGA), SP(GAUGA), and SP(SPHGA), exactly
two spatial coordinate variables must be specified as 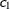 and
and 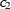 . Geometric anisotropy is corrected by applying a rotation
. Geometric anisotropy is corrected by applying a rotation 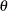 and scaling
and scaling 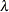 to the coordinate system, and
to the coordinate system, and 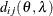 represents the Euclidean distance between two points in the transformed space. SP(MATERN) and SP(MATHSW) represent covariance
structures in a class defined by Matérn (see Matérn 1986; Handcock and Stein 1993; Handcock and Wallis 1994). The function
represents the Euclidean distance between two points in the transformed space. SP(MATERN) and SP(MATHSW) represent covariance
structures in a class defined by Matérn (see Matérn 1986; Handcock and Stein 1993; Handcock and Wallis 1994). The function 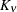 is the modified Bessel function of the second kind of (real) order
is the modified Bessel function of the second kind of (real) order 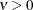 ; the parameter
; the parameter  governs the smoothness of the process (see below for more details).
governs the smoothness of the process (see below for more details).
Table 63.19 lists some examples of the structures in Table 63.17 and Table 63.18.
Table 63.19: Covariance Structure Examples
Description
Structure
Example
Variance
componentsVC (default)
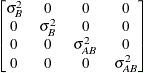
Compound
symmetryCS
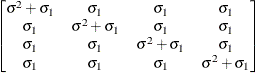
Unstructured
UN
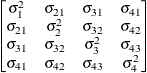
Banded main
diagonalUN(1)
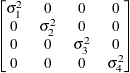
First-order
autoregressiveAR(1)
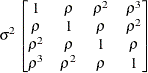
Toeplitz
TOEP
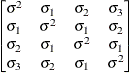
Toeplitz with
two bandsTOEP(2)
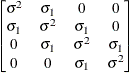
Spatial
powerSP(POW)(c)
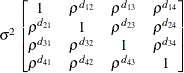
Heterogeneous
AR(1)ARH(1)
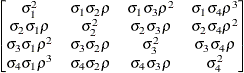
First-order
autoregressive
moving averageARMA(1,1)
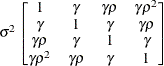
Heterogeneous
CSCSH
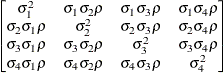
First-order
factor
analyticFA(1)
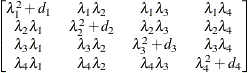
Huynh-Feldt
HF
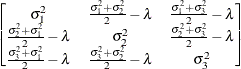
First-order
antedependenceANTE(1)
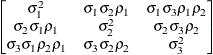
Heterogeneous
ToeplitzTOEPH
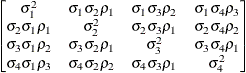
Unstructured
correlationsUNR
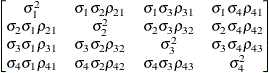
Direct product
AR(1)UN@AR(1)
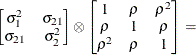
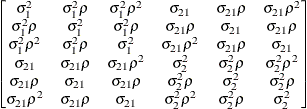
The following provides some further information about these covariance structures:
- ANTE(1)
-
specifies the first-order antedependence structure (see Kenward 1987; Patel 1991; Macchiavelli and Arnold 1994). In Table 63.17,
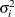 is the ith variance parameter, and
is the ith variance parameter, and 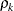 is the kth autocorrelation parameter satisfying
is the kth autocorrelation parameter satisfying 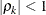 .
.
- AR(1)
-
specifies a first-order autoregressive structure. PROC MIXED imposes the constraint
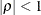 for stationarity.
for stationarity.
- ARH(1)
-
specifies a heterogeneous first-order autoregressive structure. As with TYPE=AR(1), PROC MIXED imposes the constraint
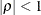 for stationarity.
for stationarity.
- ARMA(1,1)
-
specifies the first-order autoregressive moving-average structure. In Table 63.17,
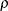 is the autoregressive parameter,
is the autoregressive parameter, 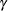 models a moving-average component, and
models a moving-average component, and 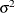 is the residual variance. In the notation of Fuller (1976, p. 68),
is the residual variance. In the notation of Fuller (1976, p. 68), 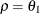 and
and
![\[ \gamma = \frac{(1 + b_1\theta _1)(\theta _1 + b_1)}{1 + b^2_1 + 2 b_1 \theta _1} \]](images/statug_mixed0272.png)
The example in Table 63.19 and
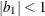 imply that
imply that
![\[ b_1 = \frac{\beta - \sqrt {\beta ^2 - 4\alpha ^2}}{2\alpha } \]](images/statug_mixed0274.png)
where
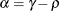 and
and 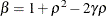 . PROC MIXED imposes the constraints
. PROC MIXED imposes the constraints 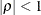 and
and 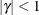 for stationarity, although for some values of
for stationarity, although for some values of 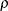 and
and 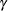 in this region the resulting covariance matrix is not positive definite. When the estimated value of
in this region the resulting covariance matrix is not positive definite. When the estimated value of 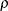 becomes negative, the computed covariance is multiplied by
becomes negative, the computed covariance is multiplied by 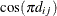 to account for the negativity.
to account for the negativity.
- CS
-
specifies the compound-symmetry structure, which has constant variance and constant covariance.
- CSH
-
specifies the heterogeneous compound-symmetry structure. This structure has a different variance parameter for each diagonal element, and it uses the square roots of these parameters in the off-diagonal entries. In Table 63.17,
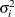 is the ith variance parameter, and
is the ith variance parameter, and 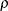 is the correlation parameter satisfying
is the correlation parameter satisfying 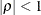 .
.
- FA(q)
-
specifies the factor-analytic structure with q factors (Jennrich and Schluchter, 1986). This structure is of the form
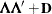 , where
, where 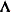 is a
is a 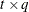 rectangular matrix and
rectangular matrix and 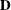 is a
is a 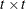 diagonal matrix with t different parameters. When q > 1, the elements of
diagonal matrix with t different parameters. When q > 1, the elements of 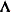 in its upper-right corner (that is, the elements in the ith row and jth column for j > i) are set to zero to fix the rotation of the structure.
in its upper-right corner (that is, the elements in the ith row and jth column for j > i) are set to zero to fix the rotation of the structure.
- FA0(q)
-
is similar to the FA(q) structure except that no diagonal matrix
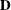 is included. When q < t—that is, when the number of factors is less than the dimension of the matrix—this structure is nonnegative definite but not
of full rank. In this situation, you can use it for approximating an unstructured
is included. When q < t—that is, when the number of factors is less than the dimension of the matrix—this structure is nonnegative definite but not
of full rank. In this situation, you can use it for approximating an unstructured 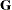 matrix in the RANDOM statement or for combining with the LOCAL option in the REPEATED statement. When q = t, you can use this structure to constrain
matrix in the RANDOM statement or for combining with the LOCAL option in the REPEATED statement. When q = t, you can use this structure to constrain 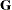 to be nonnegative definite in the RANDOM statement.
to be nonnegative definite in the RANDOM statement.
- FA1(q)
-
is similar to the TYPE=FA(q) structure except that all of the elements in
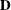 are constrained to be equal. This offers a useful and more parsimonious alternative to the full factor-analytic structure.
are constrained to be equal. This offers a useful and more parsimonious alternative to the full factor-analytic structure.
- HF
-
specifies the Huynh-Feldt covariance structure (Huynh and Feldt, 1970). This structure is similar to the TYPE=CSH structure in that it has the same number of parameters and heterogeneity along the main diagonal. However, it constructs the off-diagonal elements by taking arithmetic rather than geometric means.
You can perform a likelihood ratio test of the Huynh-Feldt conditions by running PROC MIXED twice, once with TYPE=HF and once with TYPE=UN, and then subtracting their respective values of –2 times the maximized likelihood.
If PROC MIXED does not converge under your Huynh-Feldt model, you can specify your own starting values with the PARMS statement. The default MIVQUE(0) starting values can sometimes be poor for this structure. A good choice for starting values is often the parameter estimates corresponding to an initial fit that uses TYPE=CS.
- LIN(q)
-
specifies the general linear covariance structure with q parameters. This structure consists of a linear combination of known matrices that are input with the LDATA= option. This structure is very general, and you need to make sure that the variance matrix is positive definite. By default, PROC MIXED sets the initial values of the parameters to 1. You can use the PARMS statement to specify other initial values.
- LINEAR(q)
-
is an alias for TYPE=LIN(q).
- SIMPLE
-
is an alias for TYPE=VC.
- SP(EXPA)(c-list)
-
specifies the spatial anisotropic exponential structure, where c-list is a list of variables indicating the coordinates. This structure has
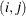 element equal to
element equal to
![\[ \sigma ^2 \prod _{k=1}^ c \exp \{ -\theta _ k d(i,j,k)^{p_ k}\} \]](images/statug_mixed0283.png)
where c is the number of coordinates and
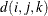 is the absolute distance between the kth coordinate (
is the absolute distance between the kth coordinate (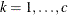 ) of the ith and jth observations in the input data set. There are 2c + 1 parameters to be estimated:
) of the ith and jth observations in the input data set. There are 2c + 1 parameters to be estimated: 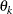 ,
, 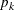 (
(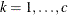 ), and
), and 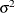 .
.
You might want to constrain some of the EXPA parameters to known values. For example, suppose you have three coordinate variables C1, C2, and C3 and you want to constrain the powers
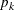 to equal 2, as in Sacks et al. (1989). Suppose further that you want to model covariance across the entire input data set and you suspect the
to equal 2, as in Sacks et al. (1989). Suppose further that you want to model covariance across the entire input data set and you suspect the 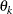 and
and 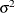 estimates are close to 3, 4, 5, and 1, respectively. Then specify the following statements:
estimates are close to 3, 4, 5, and 1, respectively. Then specify the following statements:
repeated / type=sp(expa)(c1 c2 c3) subject=intercept; parms (3) (4) (5) (2) (2) (2) (1) / hold=4,5,6;
- SP(EXPGA)(
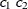 )
) -
specify modification of the isotropic SP(EXP) covariance structure.
- SP(GAUGA)(
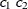 )
) -
specify modification of the isotropic SP(GAU) covariance structure.
- SP(SPHGA)(
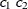 )
) -
specify modification of the isotropic SP(SPH) covariance structure.
These are structures that allow for geometric anisotropy in two dimensions. The coordinates are specified by the variables
c1andc2.If the spatial process is geometrically anisotropic in
![$\mb {c}=[c_{i1}, c_{i2}]$](images/statug_mixed0288.png) , then it is isotropic in the coordinate system
, then it is isotropic in the coordinate system
![\[ \mb {Ac} = \left[ \begin{array}{cc} 1 & 0 \\ 0 & \lambda \end{array}\right] \left[ \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right] \mb {c} = \mb {c}^* \]](images/statug_mixed0289.png)
for a properly chosen angle
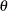 and scaling factor
and scaling factor 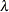 . Elliptical isocorrelation contours are thereby transformed to spherical contours, adding two parameters to the respective
isotropic covariance structures. Euclidean distances (see Table 63.18) are expressed in terms of
. Elliptical isocorrelation contours are thereby transformed to spherical contours, adding two parameters to the respective
isotropic covariance structures. Euclidean distances (see Table 63.18) are expressed in terms of 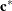 .
.
The angle
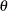 of the clockwise rotation is reported in radians,
of the clockwise rotation is reported in radians, 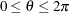 . The scaling parameter
. The scaling parameter 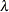 represents the ratio of the range parameters in the direction of the major and minor axis of the correlation contours. In
other words, following a rotation of the coordinate system by angle
represents the ratio of the range parameters in the direction of the major and minor axis of the correlation contours. In
other words, following a rotation of the coordinate system by angle 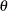 , isotropy is achieved by compressing or magnifying distances in one coordinate by the factor
, isotropy is achieved by compressing or magnifying distances in one coordinate by the factor 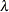 .
.
Fixing
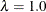 reduces the models to isotropic ones for any angle of rotation. If the scaling parameter is held constant at 1.0, you should
also hold constant the angle of rotation, as in the following statements:
reduces the models to isotropic ones for any angle of rotation. If the scaling parameter is held constant at 1.0, you should
also hold constant the angle of rotation, as in the following statements:
repeated / type=sp(expga)(gxc gyc) subject=intercept; parms (6) (1.0) (0.0) (1) / hold=2,3;If
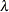 is fixed at any other value than 1.0, the angle of rotation can be estimated. Specifying a starting grid of angles and scaling
factors can considerably improve the convergence properties of the optimization algorithm for these models. Only a single
random effect with geometrically anisotropic structure is permitted.
is fixed at any other value than 1.0, the angle of rotation can be estimated. Specifying a starting grid of angles and scaling
factors can considerably improve the convergence properties of the optimization algorithm for these models. Only a single
random effect with geometrically anisotropic structure is permitted.
- SP(MATERN)(c-list ) | SP(MATHSW)(c-list )
-
specifies covariance structures in the Matérn class of covariance functions (Matérn, 1986). Two observations for the same subject (block of
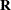 ) that are Euclidean distance
) that are Euclidean distance 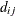 apart have covariance
apart have covariance
![\[ \sigma ^2 \frac{1}{\Gamma (\nu )} \left(\frac{d_{ij}}{2\rho }\right)^\nu 2 K_\nu (d_{ij}/\rho ) \qquad \nu > 0, \, \, \rho > 0 \]](images/statug_mixed0293.png)
where
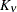 is the modified Bessel function of the second kind of (real) order
is the modified Bessel function of the second kind of (real) order 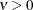 . The smoothness (continuity) of a stochastic process with covariance function in this class increases with
. The smoothness (continuity) of a stochastic process with covariance function in this class increases with  . The Matérn class thus enables data-driven estimation of the smoothness properties. The covariance is identical to the exponential
model for
. The Matérn class thus enables data-driven estimation of the smoothness properties. The covariance is identical to the exponential
model for 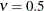 (TYPE=SP(EXP)(c-list)), while for
(TYPE=SP(EXP)(c-list)), while for 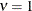 the model advocated by Whittle (1954) results. As
the model advocated by Whittle (1954) results. As 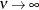 the model approaches the gaussian covariance structure (TYPE=SP(GAU)(c-list)).
the model approaches the gaussian covariance structure (TYPE=SP(GAU)(c-list)).
The MATHSW structure represents the Matérn class in the parameterization of Handcock and Stein (1993) and Handcock and Wallis (1994),
![\[ \sigma ^2\frac{1}{\Gamma (\nu )} \left(\frac{d_{ij}\sqrt {\nu }}{\rho }\right)^{\nu } 2 K_{\nu }\left(\frac{2d_{ij}\sqrt {\nu }}{\rho }\right) \]](images/statug_mixed0298.png)
Since computation of the function
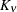 and its derivatives is numerically very intensive, fitting models with Matérn covariance structures can be more time-consuming
than with other spatial covariance structures. Good starting values are essential.
and its derivatives is numerically very intensive, fitting models with Matérn covariance structures can be more time-consuming
than with other spatial covariance structures. Good starting values are essential.
- SP(POW)(c-list) | SP(POWA)(c-list)
-
specifies the spatial power structures. When the estimated value of
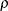 becomes negative, the computed covariance is multiplied by
becomes negative, the computed covariance is multiplied by 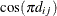 to account for the negativity.
to account for the negativity.
- TOEP<(q)>
-
specifies a banded Toeplitz structure. This can be viewed as a moving-average structure with order equal to
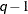 . The TYPE=TOEP option is a full Toeplitz matrix, which can be viewed as an autoregressive structure with order equal to the
dimension of the matrix. The specification TYPE=TOEP(1) is the same as
. The TYPE=TOEP option is a full Toeplitz matrix, which can be viewed as an autoregressive structure with order equal to the
dimension of the matrix. The specification TYPE=TOEP(1) is the same as 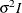 , where I is an identity matrix, and it can be useful for specifying the same variance component for several effects.
, where I is an identity matrix, and it can be useful for specifying the same variance component for several effects.
- TOEPH<(q)>
-
specifies a heterogeneous banded Toeplitz structure. In Table 63.17,
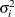 is the ith variance parameter and
is the ith variance parameter and 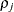 is the jth correlation parameter satisfying
is the jth correlation parameter satisfying 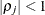 . If you specify the order parameter q, then PROC MIXED estimates only the first q bands of the matrix, setting all higher bands equal to 0. The option TOEPH(1) is equivalent to both the TYPE=UN(1) and TYPE=UNR(1) options.
. If you specify the order parameter q, then PROC MIXED estimates only the first q bands of the matrix, setting all higher bands equal to 0. The option TOEPH(1) is equivalent to both the TYPE=UN(1) and TYPE=UNR(1) options.
- UN<(q)>
-
specifies a completely general (unstructured) covariance matrix parameterized directly in terms of variances and covariances. The variances are constrained to be nonnegative, and the covariances are unconstrained. This structure is not constrained to be nonnegative definite in order to avoid nonlinear constraints; however, you can use the TYPE=FA0 structure if you want this constraint to be imposed by a Cholesky factorization. If you specify the order parameter q, then PROC MIXED estimates only the first q bands of the matrix, setting all higher bands equal to 0.
- UNR<(q)>
-
specifies a completely general (unstructured) covariance matrix parameterized in terms of variances and correlations. This structure fits the same model as the TYPE=UN(q) option but with a different parameterization. The ith variance parameter is
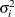 . The parameter
. The parameter 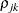 is the correlation between the jth and kth measurements; it satisfies
is the correlation between the jth and kth measurements; it satisfies 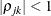 . If you specify the order parameter r, then PROC MIXED estimates only the first q bands of the matrix, setting all higher bands equal to zero.
. If you specify the order parameter r, then PROC MIXED estimates only the first q bands of the matrix, setting all higher bands equal to zero.
- UN@AR(1) | UN@CS | UN@UN
-
specify direct (Kronecker) product structures designed for multivariate repeated measures (see Galecki 1994). These structures are constructed by taking the Kronecker product of an unstructured matrix (modeling covariance across the multivariate observations) with an additional covariance matrix (modeling covariance across time or another factor). The upper-left value in the second matrix is constrained to equal 1 to identify the model. See the SAS/IML User's Guide for more details about direct products.
To use these structures in the REPEATED statement, you must specify two distinct REPEATED effects, both of which must be included in the CLASS statement. The first effect indicates the multivariate observations, and the second identifies the levels of time or some additional factor. Note that the input data set must still be constructed in “univariate” format; that is, all dependent observations are still listed observation-wise in one single variable. Although this construction provides for general modeling possibilities, it forces you to construct variables indicating both dimensions of the Kronecker product.
For example, suppose your observed data consist of heights and weights of several children measured over several successive years. Your input data set should then contain variables similar to the following:
-
Y, all of the heights and weights, with a separate observation for each -
Var, indicating whether the measurement is a height or a weight -
Year, indicating the year of measurement -
Child, indicating the child on which the measurement was taken
Your PROC MIXED statements for a Kronecker AR(1) structure across years would then be as follows:
proc mixed; class Var Year Child; model Y = Var Year Var*Year; repeated Var Year / type=un@ar(1) subject=Child; run;You should nearly always want to model different means for the multivariate observations; hence the inclusion of
Varin the MODEL statement. The preceding mean model consists of cell means for all combinations ofVARandYEAR. -
- VC
-
specifies standard variance components and is the default structure for both the RANDOM and REPEATED statements. In the RANDOM statement, a distinct variance component is assigned to each effect. In the REPEATED statement, this structure is usually used only with the GROUP= option to specify a heterogeneous variance model.
Jennrich and Schluchter (1986) provide general information about the use of covariance structures, and Wolfinger (1996) presents details about many of the heterogeneous structures. Modeling with spatial covariance structures is discussed in many sources (Marx and Thompson, 1987; Zimmerman and Harville, 1991; Cressie, 1993; Brownie, Bowman, and Burton, 1993; Stroup, Baenziger, and Mulitze, 1994; Brownie and Gumpertz, 1997; Gotway and Stroup, 1997; Chilès and Delfiner, 1999; Schabenberger and Gotway, 2005; Littell et al., 2006).
