-
ADJDFE=SOURCE | ROW
-
specifies how denominator degrees of freedom are determined when
p-values and confidence limits are adjusted for multiple comparisons with the ADJUST= option. When you do not specify the ADJDFE= option, or when you specify ADJDFE=SOURCE, the denominator degrees of freedom
for multiplicity-adjusted results are the denominator degrees of freedom for the LS-mean effect in the “Type 3 Tests of Fixed Effects” table. When you specify ADJDFE=ROW, the denominator degrees of freedom for multiplicity-adjusted results correspond to the
degrees of freedom displayed in the DF column of the “Differences of Least Squares Means” table.
The ADJDFE=ROW setting is particularly useful if you want multiplicity adjustments to take into account that denominator degrees
of freedom are not constant across LS-mean differences. This can be the case, for example, when the DDFM=SATTERTHWAITE or DDFM=KENWARDROGER degrees-of-freedom method is in effect.
In one-way models with heterogeneous variance, combining certain ADJUST= options with the ADJDFE=ROW option corresponds to particular methods of performing multiplicity adjustments in the presence
of heteroscedasticity. For example, the following statements fit a heteroscedastic one-way model and perform Dunnett’s T3
method (Dunnett, 1980), which is based on the studentized maximum modulus (ADJUST=SMM):
proc mixed;
class A;
model y = A / ddfm=satterth;
repeated / group=A;
lsmeans A / adjust=smm adjdfe=row;
run;
If you combine the ADJDFE=ROW option with ADJUST=SIDAK, the multiplicity adjustment corresponds to the T2 method of Tamhane (1979), while ADJUST=TUKEY corresponds to the method of Games-Howell (Games and Howell, 1976). Note that ADJUST=TUKEY gives the exact results for the case of fractional degrees of freedom in the one-way model, but it does not take into
account that the degrees of freedom are subject to variability. A more conservative method, such as ADJUST=SMM, might protect the overall error rate better.
Unless the ADJUST= option of the LSMEANS statement is specified, the ADJDFE= option has no effect.
-
ADJUST=BON
ADJUST=DUNNETT
ADJUST=SCHEFFE
ADJUST=SIDAK
ADJUST=SIMULATE<(sim-options)>
ADJUST=SMM | GT2
ADJUST=TUKEY
-
requests a multiple comparison adjustment for the p-values and
confidence limits for the differences of LS-means. By default, PROC MIXED adjusts all pairwise differences unless you specify
ADJUST=DUNNETT, in which case PROC MIXED analyzes all differences with a control level. The ADJUST= option implies the DIFF option.
The BON (Bonferroni) and SIDAK adjustments involve correction factors described in Chapter 44: The GLM Procedure, and Chapter 65: The MULTTEST Procedure; also see Westfall and Young (1993) and Westfall et al. (1999). When you specify ADJUST=TUKEY and your data are unbalanced, PROC MIXED uses the approximation described in Kramer (1956). Similarly, when you specify ADJUST=DUNNETT and the LS-means are correlated, PROC MIXED uses the factor-analytic covariance
approximation described in Hsu (1992). The preceding references also describe the SCHEFFE and SMM adjustments.
The SIMULATE adjustment computes adjusted p-values and confidence limits from the simulated distribution of the maximum or maximum absolute value of a multivariate t random vector. All covariance parameters except the residual variance are fixed at their estimated values throughout the
simulation, potentially resulting in some underdispersion. The simulation estimates q, the true 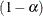 quantile, where
quantile, where 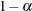 is the confidence coefficient. The default
is the confidence coefficient. The default  is 0.05, and you can change this value with the ALPHA= option in the LSMEANS statement.
is 0.05, and you can change this value with the ALPHA= option in the LSMEANS statement.
The number of samples is set so that the tail area for the simulated q is within 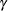 of
of 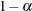 with
with 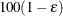 % confidence. In equation form,
% confidence. In equation form,
where 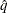 is the simulated q and F is the true distribution function of the maximum; see Edwards and Berry (1987) for details. By default,
is the simulated q and F is the true distribution function of the maximum; see Edwards and Berry (1987) for details. By default, 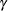 = 0.005 and
= 0.005 and  = 0.01, placing the tail area of
= 0.01, placing the tail area of 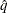 within 0.005 of 0.95 with 99% confidence. The ACC= and EPS= sim-options reset
within 0.005 of 0.95 with 99% confidence. The ACC= and EPS= sim-options reset 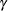 and
and  , respectively; the NSAMP= sim-option sets the sample size directly; and the SEED= sim-option specifies an integer used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or
if you specify a value less than or equal to zero, the seed is generated from reading the time of day from the computer clock.
For additional descriptions of these and other simulation options, see the section LSMEANS Statement in Chapter 44: The GLM Procedure.
, respectively; the NSAMP= sim-option sets the sample size directly; and the SEED= sim-option specifies an integer used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or
if you specify a value less than or equal to zero, the seed is generated from reading the time of day from the computer clock.
For additional descriptions of these and other simulation options, see the section LSMEANS Statement in Chapter 44: The GLM Procedure.
-
ALPHA=number
-
requests that a t-type confidence interval be constructed for
each of the LS-means with confidence level 1 – number. The value of number must be between 0 and 1; the default is 0.05.
-
AT variable = value
AT (variable-list)= (value-list)
AT MEANS
-
enables you to modify the values of the covariates used in computing
LS-means. By default, all covariate effects are set equal to their mean values for computation of standard LS-means. The AT
option enables you to assign arbitrary values to the covariates. Additional columns in the output table indicate the values
of the covariates.
If there is an effect containing two or more covariates, the AT option sets the effect equal to the product of the individual
means rather than the mean of the product (as with standard LS-means calculations). The AT MEANS option sets covariates equal
to their mean values (as with standard LS-means) and incorporates this adjustment to crossproducts of covariates.
As an example, consider the following invocation of PROC MIXED:
proc mixed;
class A;
model Y = A X1 X2 X1*X2;
lsmeans A;
lsmeans A / at means;
lsmeans A / at X1=1.2;
lsmeans A / at (X1 X2)=(1.2 0.3);
run;
For the first two LSMEANS statements, the LS-means coefficient for X1 is 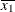 (the mean of
(the mean of X1) and for X2 is 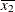 (the mean of
(the mean of X2). However, for the first LSMEANS statement, the coefficient for X1*X2 is 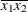 , but for the second LSMEANS statement, the coefficient is
, but for the second LSMEANS statement, the coefficient is 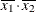 . The third LSMEANS statement sets the coefficient for
. The third LSMEANS statement sets the coefficient for X1 equal to 1.2 and leaves it at 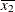 for
for X2, and the final LSMEANS statement sets these values to 1.2 and 0.3, respectively.
If a WEIGHT variable is present, it is used in processing AT variables. Also, observations with missing dependent variables
are included in computing the covariate means, unless these observations form a missing cell and the FULLX option in the MODEL statement is not in effect. You can use the E option in conjunction with the AT option to check that the modified LS-means coefficients are the ones you want.
The AT option is disabled if you specify the BYLEVEL option.
-
BYLEVEL
-
requests PROC MIXED to process the OM data set
by each level of the LS-mean effect (LSMEANS effect) in question. For more details, see the OM option later in this section.
-
CL
-
requests that t-type confidence limits be constructed for each
of the LS-means. The confidence level is 0.95 by default; this can be changed with the ALPHA= option.
-
CORR
-
displays the estimated correlation matrix of the least squares means
as part of the “Least Squares Means” table.
-
COV
-
displays the estimated covariance matrix of the least squares means
as part of the “Least Squares Means” table.
-
DF=number
-
specifies the degrees of freedom for the t test and
confidence limits. The default is the denominator degrees of freedom taken from the “Tests of Fixed Effects” table corresponding to the LS-means effect unless the DDFM=SATTERTHWAITE or DDFM=KENWARDROGER option is in effect in the MODEL statement. For these DDFM= methods, degrees of freedom are determined separately for each test; see the DDFM= option for more information.
-
DIFF<=difftype>
PDIFF<=difftype>
-
requests that differences of the LS-means be displayed. The optional
difftype specifies which differences to produce, with possible values being ALL, CONTROL, CONTROLL, and CONTROLU. The difftype ALL requests all pairwise differences, and it is the default. The difftype CONTROL requests the differences with a control, which, by default, is the first level of each of the specified LSMEANS effects.
To specify which levels of the effects are the controls, list the quoted formatted values in parentheses after the keyword
CONTROL. For example, if the effects A, B, and C are classification variables, each having two levels, 1 and 2, the following LSMEANS statement specifies the (1,2) level
of A*B and the (2,1) level of B*C as controls:
lsmeans A*B B*C / diff=control('1' '2' '2' '1');
For multiple effects, the results depend upon the order of the list, and so you should check the output to make sure that
the controls are correct.
Two-tailed tests and confidence limits are associated with the CONTROL difftype. For one-tailed results, use either the CONTROLL or CONTROLU difftype. The CONTROLL difftype tests whether the noncontrol levels are significantly smaller than the control; the upper confidence limits for the control
minus the noncontrol levels are considered to be infinity and are displayed as missing. Conversely, the CONTROLU difftype tests whether the noncontrol levels are significantly larger than the control; the upper confidence limits for the noncontrol
levels minus the control are considered to be infinity and are displayed as missing.
If you want to perform multiple comparison adjustments on the differences of LS-means, you must specify the ADJUST= option.
The differences of the LS-means are displayed in a table titled “Differences of Least Squares Means.” The ODS table name is Diffs.
-
E
-
requests that the  matrix coefficients for all LSMEANS effects
be displayed. The ODS name of this “
matrix coefficients for all LSMEANS effects
be displayed. The ODS name of this “ Matrix Coefficients” table is Coef.
Matrix Coefficients” table is Coef.
-
OM<=OM-data-set>
OBSMARGINS<=OM-data-set>
-
specifies a potentially different weighting scheme for the
computation of LS-means coefficients. The standard LS-means have equal coefficients across classification effects; however,
the OM option changes these coefficients to be proportional to those found in OM-data-set. This adjustment is reasonable when you want your inferences to apply to a population that is not necessarily balanced but
has the margins observed in OM-data-set.
By default, OM-data-set is the same as the analysis data set. You can optionally specify another data set that describes the population for which
you want to make inferences. This data set must contain all model variables except for the dependent variable (which is ignored
if it is present). In addition, the levels of all CLASS variables must be the same as those occurring in the analysis data set. Specifying an OM-data-set enables you to construct arbitrarily weighted LS-means.
In computing the observed margins, PROC MIXED uses all observations for which there are no missing or invalid independent
variables, including those for which there are missing dependent variables. Also, if OM-data-set has a WEIGHT variable, PROC MIXED uses weighted margins to construct the LS-means coefficients. If OM-data-set is balanced, the LS-means are unchanged by the OM option.
The BYLEVEL option modifies the observed-margins LS-means. Instead of computing the margins across all of the OM-data-set, PROC MIXED computes separate margins for each level of the LSMEANS effect in question. In this case the resulting LS-means
are actually equal to raw means for fixed-effects models and certain balanced random-effects models, but their estimated standard
errors account for the covariance structure that you have specified. If the AT option is specified, the BYLEVEL option disables it.
You can use the E option in conjunction with either the OM or BYLEVEL option to check that the modified LS-means coefficients are the ones you want. It is possible that the modified LS-means
are not estimable when the standard ones are, or vice versa. Nonestimable LS-means are noted as “Non-est” in the output.
-
PDIFF
-
is the same as the DIFF option.
-
SINGULAR=number
-
tunes the estimability checking as documented for the
SINGULAR= option in the CONTRAST statement.
-
SLICE= fixed-effect | (fixed-effects)
-
specifies effects by which to partition interaction LSMEANS effects.
This can produce what are known as tests of simple effects (Winer, 1971). For example, suppose that A*B is significant, and you want to test the effect of A for each level of B. The appropriate LSMEANS statement is as follows:
lsmeans A*B / slice=B;
This code tests for the simple main effects of A for B, which are calculated by extracting the appropriate rows from the coefficient matrix for the A*B LS-means and by using them to form an F test. See the section Inference and Test Statistics for more information about this F test.
The SLICE option produces a table titled “Tests of Effect Slices.” The ODS table name is Slices.
![]() matrix constructed to compute them is the same as the
matrix constructed to compute them is the same as the ![]() matrix formed in PROC GLM; however, the standard errors are adjusted for the covariance parameters in the model.
matrix formed in PROC GLM; however, the standard errors are adjusted for the covariance parameters in the model.
![]() , where
, where ![]() is the coefficient matrix associated with the least squares mean and
is the coefficient matrix associated with the least squares mean and ![]() is the estimate of the fixed-effects parameter vector (see the section Estimating Fixed and Random Effects in the Mixed Model). The approximate standard errors for the LS-mean is computed as the square root of
is the estimate of the fixed-effects parameter vector (see the section Estimating Fixed and Random Effects in the Mixed Model). The approximate standard errors for the LS-mean is computed as the square root of ![]() .
.
![]() matrix is tested for estimability, and if this test fails, PROC MIXED displays “Non-est” for the LS-means entries.
matrix is tested for estimability, and if this test fails, PROC MIXED displays “Non-est” for the LS-means entries.
