Mixed Models Theory
Previous Page|Next Page

The MIXED Procedure

Mixed Models Theory

Subsections:

This section provides an overview of a likelihood-based approach to general linear mixed models. This approach simplifies and unifies many common statistical analyses, including those involving repeated measures, random effects, and random coefficients. The basic assumption is that the data are linearly related to unobserved multivariate normal random variables. For extensions to nonlinear and nonnormal situations see the documentation of the GLIMMIX and NLMIXED procedures. Additional theory and examples are provided in Littell et al. (2006); Verbeke and Molenberghs (1997, 2000); Brown and Prescott (1999).

Matrix Notation

Suppose that you observe n data points $y_1, \ldots , y_ n$ and that you want to explain them by using n values for each of p explanatory variables $x_{11}, \ldots , x_{1p}$, $x_{21}, \ldots , x_{2p}$, $\ldots , x_{n1}, \ldots , x_{np}$. The $x_{ij}$ values can be either regression-type continuous variables or dummy variables indicating class membership. The standard linear model for this setup is

\[ y_ i = \sum _{j=1}^ p x_{ij} \beta _ j + \epsilon _ i \quad i=1,\ldots ,n \]

where $\beta _1, \ldots , \beta _ p$ are unknown fixed-effects parameters to be estimated and $\epsilon _1, \ldots , \epsilon _ n$ are unknown independent and identically distributed normal (Gaussian) random variables with mean 0 and variance $\sigma ^2$.

The preceding equations can be written simultaneously by using vectors and a matrix, as follows:

\[ \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_ n \end{array} \right] = \left[\begin{array}{cccc} x_{11} & x_{12} & \ldots & x_{1p} \\ x_{21} & x_{22} & \ldots & x_{2p} \\ \vdots & \vdots & & \vdots \\ x_{n1} & x_{n2} & \ldots & x_{np} \end{array} \right] \left[\begin{array}{c} \beta _1 \\ \beta _2 \\ \vdots \\ \beta _ p \end{array} \right] + \left[\begin{array}{c} \epsilon _1 \\ \epsilon _2 \\ \vdots \\ \epsilon _ n \end{array} \right] \]

For convenience, simplicity, and extendability, this entire system is written as

\[ \mb {y} = \mb {X}\bbeta + \bepsilon \]

where $\mb {y}$ denotes the vector of observed $y_ i$’s, $\mb {X}$ is the known matrix of $x_{ij}$’s, $\bbeta $ is the unknown fixed-effects parameter vector, and $\bepsilon $ is the unobserved vector of independent and identically distributed Gaussian random errors.

In addition to denoting data, random variables, and explanatory variables in the preceding fashion, the subsequent development makes use of basic matrix operators such as transpose ($’$), inverse ($^{-1}$), generalized inverse ($^{-}$), determinant ($|\cdot |$), and matrix multiplication. See Searle (1982) for details about these and other matrix techniques.

Formulation of the Mixed Model

The previous general linear model is certainly a useful one (Searle, 1971), and it is the one fitted by the GLM procedure. However, many times the distributional assumption about $\epsilon $ is too restrictive. The mixed model extends the general linear model by allowing a more flexible specification of the covariance matrix of $\epsilon $. In other words, it allows for both correlation and heterogeneous variances, although you still assume normality.

The mixed model is written as

\[ \mb {y} = \mb {X}\bbeta + \mb {Z}\bgamma +\bepsilon \]

where everything is the same as in the general linear model except for the addition of the known design matrix, $\mb {Z}$, and the vector of unknown random-effects parameters, $\bgamma $. The matrix $\mb {Z}$ can contain either continuous or dummy variables, just like $\mb {X}$. The name mixed model comes from the fact that the model contains both fixed-effects parameters, $\bbeta $, and random-effects parameters, $\bgamma $. See Henderson (1990) and Searle, Casella, and McCulloch (1992) for historical developments of the mixed model.

A key assumption in the foregoing analysis is that $\bgamma $ and $\bepsilon $ are normally distributed with

\begin{align*} \mr {E}\left[ \begin{array}{c} \bgamma \\ \bepsilon \end{array} \right] & = \left[\begin{array}{c} \Strong{0} \\ \Strong{0} \end{array} \right] \\ \mr {Var}\left[ \begin{array}{c} \bgamma \\ \bepsilon \end{array} \right] & = \left[\begin{array}{cc} \mb {G} & \Strong{0} \\ \Strong{0} & \mb {R} \end{array} \right] \end{align*}

The variance of $\mb {y}$ is, therefore, $\mb {V} = \mb {ZGZ}’ + \mb {R}$. You can model $\mb {V}$ by setting up the random-effects design matrix $\mb {Z}$ and by specifying covariance structures for $\mb {G}$ and $\mb {R}$.

Note that this is a general specification of the mixed model, in contrast to many texts and articles that discuss only simple random effects. Simple random effects are a special case of the general specification with $\mb {Z}$ containing dummy variables, $\mb {G}$ containing variance components in a diagonal structure, and $\mb {R} = \sigma ^2\mb {I} _ n$, where $\mb {I} _ n$ denotes the $n \times n$ identity matrix. The general linear model is a further special case with $\mb {Z} = \mb {0} $ and $\mb {R} = \sigma ^2\mb {I} _ n$.

The following two examples illustrate the most common formulations of the general linear mixed model.

Example: Growth Curve with Compound Symmetry

Suppose that you have three growth curve measurements for s individuals and that you want to fit an overall linear trend in time. Your $\mb {X}$ matrix is as follows:

\[ \mb {X} = \left[ \begin{array}{rr} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \vdots & \vdots \\ 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \end{array} \right] \]

The first column (coded entirely with 1s) fits an intercept, and the second column (coded with times of $1,2,3$) fits a slope. Here, $n = 3s$ and $p = 2$.

Suppose further that you want to introduce a common correlation among the observations from a single individual, with correlation being the same for all individuals. One way of setting this up in the general mixed model is to eliminate the $\mb {Z}$ and $\mb {G}$ matrices and let the $\mb {R}$ matrix be block diagonal with blocks corresponding to the individuals and with each block having the compound-symmetry structure. This structure has two unknown parameters, one modeling a common covariance and the other modeling a residual variance. The form for $\mb {R}$ would then be as follows:

\[ \mb {R} = \left[ \begin{array}{ccccccc} \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 & \sigma ^2_1 & & & & \\ \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 & & & & \\ \sigma ^2_1 & \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 & & & & \\ & & & \ddots & & & \\ & & & & \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 & \sigma ^2_1 \\ & & & & \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 \\ & & & & \sigma ^2_1 & \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 \\ \end{array} \right] \]

where blanks denote zeros. There are $3s$ rows and columns altogether, and the common correlation is $\sigma ^2_1/(\sigma ^2_1 + \sigma ^2)$.

The PROC MIXED statements to fit this model are as follows: 

proc mixed;
   class indiv;
   model y = time;
   repeated / type=cs subject=indiv;
run;

Here, indiv is a classification variable indexing individuals. The MODEL statement fits a straight line for time ; the intercept is fit by default just as in PROC GLM. The REPEATED statement models the $\mb {R}$ matrix: TYPE=CS specifies the compound symmetry structure, and SUBJECT=INDIV specifies the blocks of $\mb {R}$.

An alternative way of specifying the common intra-individual correlation is to let

\begin{align*} \mb {Z} & = \left[ \begin{array}{cccc} 1 & & & \\ 1 & & & \\ 1 & & & \\ & 1 & & \\ & 1 & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \\ & & & 1 \\ & & & 1 \\ \end{array} \right] \\ \mb {G} & = \left[ \begin{array}{cccc} \sigma ^2_1 & & & \\ & \sigma ^2_1 & & \\ & & \ddots & \\ & & & \sigma ^2_1 \\ \end{array} \right] \end{align*}

and $\mb {R} = \sigma ^2\mb {I} _ n$. The $\mb {Z}$ matrix has $3s$ rows and s columns, and $\mb {G}$ is $s \times s$.

You can set up this model in PROC MIXED in two different but equivalent ways: 

proc mixed;
   class indiv;
   model y = time;
   random indiv;
run;

proc mixed;
   class indiv;
   model y = time;
   random intercept / subject=indiv;
run;

Both of these specifications fit the same model as the previous one that used the REPEATED statement; however, the RANDOM specifications constrain the correlation to be positive, whereas the REPEATED specification leaves the correlation unconstrained.

Example: Split-Plot Design

The split-plot design involves two experimental treatment factors, A and B, and two different sizes of experimental units to which they are applied (see Winer 1971; Snedecor and Cochran 1980; Milliken and Johnson 1992; Steel, Torrie, and Dickey 1997). The levels of A are randomly assigned to the larger-sized experimental unit, called whole plots, whereas the levels of B are assigned to the smaller-sized experimental unit, the subplots. The subplots are assumed to be nested within the whole plots, so that a whole plot consists of a cluster of subplots and a level of A is applied to the entire cluster.

Such an arrangement is often necessary by nature of the experiment, the classical example being the application of fertilizer to large plots of land and different crop varieties planted in subdivisions of the large plots. For this example, fertilizer is the whole-plot factor A and variety is the subplot factor B.

The first example is a split-plot design for which the whole plots are arranged in a randomized block design. The appropriate PROC MIXED statements are as follows: 

proc mixed;
   class a b block;
   model y = a|b;
   random block a*block;
run;

Here

\[ \bR = \sigma ^2 \mb {I} _{24} \]

and $\bX $, $\bZ $, and $\bG $ have the following form:

\[ \bX = \left[ \begin{array}{cccccccccccc} 1 & 1 & & & 1 & & 1 & & & & & \\ 1 & 1 & & & & 1 & & 1 & & & & \\ 1 & & 1 & & 1 & & & & 1 & & & \\ 1 & & 1 & & & 1 & & & & 1 & & \\ 1 & & & 1 & 1 & & & & & & 1 & \\ 1 & & & 1 & & 1 & & & & & & 1 \\ \vdots & & \vdots & & \vdots & & & & & \vdots \\ 1 & 1 & & & 1 & & 1 & & & & & \\ 1 & 1 & & & & 1 & & 1 & & & & \\ 1 & & 1 & & 1 & & & & 1 & & & \\ 1 & & 1 & & & 1 & & & & 1 & & \\ 1 & & & 1 & 1 & & & & & & 1 & \\ 1 & & & 1 & & 1 & & & & & & 1 \\ \end{array} \right] \\ \]
\[ \bZ \, = \left[ \begin{array}{cccccccccccccccc} 1 & & & & 1 & & & & & & & & & & & \\ 1 & & & & 1 & & & & & & & & & & & \\ 1 & & & & & 1 & & & & & & & & & & \\ 1 & & & & & 1 & & & & & & & & & & \\ 1 & & & & & & 1 & & & & & & & & & \\ 1 & & & & & & 1 & & & & & & & & & \\ & 1 & & & & & & 1 & & & & & & & & \\ & 1 & & & & & & 1 & & & & & & & & \\ & 1 & & & & & & & 1 & & & & & & & \\ & 1 & & & & & & & 1 & & & & & & & \\ & 1 & & & & & & & & 1 & & & & & & \\ & 1 & & & & & & & & 1 & & & & & & \\ & & 1 & & & & & & & & 1 & & & & & \\ & & 1 & & & & & & & & 1 & & & & & \\ & & 1 & & & & & & & & & 1 & & & & \\ & & 1 & & & & & & & & & 1 & & & & \\ & & 1 & & & & & & & & & & 1 & & & \\ & & 1 & & & & & & & & & & 1 & & & \\ & & & 1 & & & & & & & & & & 1 & & \\ & & & 1 & & & & & & & & & & 1 & & \\ & & & 1 & & & & & & & & & & & 1 & \\ & & & 1 & & & & & & & & & & & 1 & \\ & & & 1 & & & & & & & & & & & & 1 \\ & & & 1 & & & & & & & & & & & & 1 \\ \end{array} \right] \\ \]
\[ \bG = \left[ \begin{array}{ccccccccc} \sigma ^2_ B & & & & & & & \\ & \sigma ^2_ B & & & & & & \\ & & \sigma ^2_ B & & & & & \\ & & & \sigma ^2_ B & & & & \\ & & & & \sigma ^2_{AB} & & & \\ & & & & & \sigma ^2_{AB} & & \\ & & & & & & \ddots & \\ & & & & & & & \sigma ^2_{AB} \\ \end{array} \right] \]

where $\sigma ^2_ B$ is the variance component for Block and $\sigma ^2_{AB}$ is the variance component for A*Block. Changing the RANDOM statement as follows fits the same model, but with $\mb {Z}$ and $\mb {G}$ sorted differently: 

random int a / subject=block;
\begin{align*} \bZ & = \left[ \begin{array}{cccccccccccccccc} 1 & 1 & & & & & & & & & & & & & & \\ 1 & 1 & & & & & & & & & & & & & & \\ 1 & & 1 & & & & & & & & & & & & & \\ 1 & & 1 & & & & & & & & & & & & & \\ 1 & & & 1 & & & & & & & & & & & & \\ 1 & & & 1 & & & & & & & & & & & & \\ & & & & 1 & 1 & & & & & & & & & & \\ & & & & 1 & 1 & & & & & & & & & & \\ & & & & 1 & & 1 & & & & & & & & & \\ & & & & 1 & & 1 & & & & & & & & & \\ & & & & 1 & & & 1 & & & & & & & & \\ & & & & 1 & & & 1 & & & & & & & & \\ & & & & & & & & 1 & 1 & & & & & & \\ & & & & & & & & 1 & 1 & & & & & & \\ & & & & & & & & 1 & & 1 & & & & & \\ & & & & & & & & 1 & & 1 & & & & & \\ & & & & & & & & 1 & & & 1 & & & & \\ & & & & & & & & 1 & & & 1 & & & & \\ & & & & & & & & & & & & 1 & 1 & & \\ & & & & & & & & & & & & 1 & 1 & & \\ & & & & & & & & & & & & 1 & & 1 & \\ & & & & & & & & & & & & 1 & & 1 & \\ & & & & & & & & & & & & 1 & & & 1 \\ & & & & & & & & & & & & 1 & & & 1 \\ \end{array} \right] \\ \bG & = \left[ \begin{array}{ccccccccccccccc} \sigma ^2_ B & & & & & & & & \\ & \sigma ^2_{AB} & & & & & & & \\ & & \sigma ^2_{AB} & & & & & & \\ & & & \sigma ^2_{AB} & & & & & \\ & & & & \ddots & & & & & \\ & & & & & \sigma ^2_ B & & & \\ & & & & & & \sigma ^2_{AB} & & \\ & & & & & & & \sigma ^2_{AB} & \\ & & & & & & & & \sigma ^2_{AB} \\ \end{array} \right] \end{align*}

Estimating Covariance Parameters in the Mixed Model

Estimation is more difficult in the mixed model than in the general linear model. Not only do you have $\bbeta $ as in the general linear model, but you have unknown parameters in $\bgamma $, $\mb {G}$, and $\mb {R}$ as well. Least squares is no longer the best method. Generalized least squares (GLS) is more appropriate, minimizing

\[ (\mb {y} - \mb {X}\bbeta )’\mb {V}^{-1}(\mb {y} - \mb {X}\bbeta ) \]

However, it requires knowledge of $\mb {V}$ and, therefore, knowledge of $\mb {G}$ and $\mb {R}$. Lacking such information, one approach is to use estimated GLS, in which you insert some reasonable estimate for $\mb {V}$ into the minimization problem. The goal thus becomes finding a reasonable estimate of $\mb {G}$ and $\mb {R}$.

In many situations, the best approach is to use likelihood-based methods, exploiting the assumption that $\bgamma $ and $\bepsilon $ are normally distributed (Hartley and Rao, 1967; Patterson and Thompson, 1971; Harville, 1977; Laird and Ware, 1982; Jennrich and Schluchter, 1986). PROC MIXED implements two likelihood-based methods: maximum likelihood (ML) and restricted/residual maximum likelihood (REML). A favorable theoretical property of ML and REML is that they accommodate data that are missing at random (Rubin, 1976; Little, 1995).

PROC MIXED constructs an objective function associated with ML or REML and maximizes it over all unknown parameters. Using calculus, it is possible to reduce this maximization problem to one over only the parameters in $\mb {G}$ and $\mb {R}$. The corresponding log-likelihood functions are as follows:

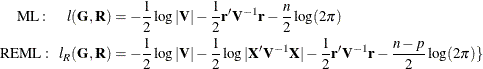
\begin{align*} \mr {ML:} \; \; \; \; \; \; l(\mb {G},\mb {R}) & = -\frac{1}{2} \log |\mb {V}| - \frac{1}{2} \Strong{r} ’\mb {V}^{-1}\Strong{r} - \frac{n}{2} \log (2 \pi ) \\ \mr {REML:} \; \; \; l_ R(\mb {G},\mb {R}) & = -\frac{1}{2} \log |\mb {V}| - \frac{1}{2} \log |\mb {X}’\mb {V}^{-1}\mb {X}| - \frac{1}{2} \Strong{r} ’\mb {V}^{-1}\Strong{r} - \frac{n-p}{2} \log (2 \pi )\} \end{align*}

where $\mb {r} = \mb {y} - \mb {X}(\bX ’\bV ^{-1}\bX )^{-}\bX ’\bV ^{-1}\mb {y}$ and p is the rank of $\bX $. PROC MIXED actually minimizes –2 times these functions by using a ridge-stabilized Newton-Raphson algorithm. Lindstrom and Bates (1988) provide reasons for preferring Newton-Raphson to the Expectation-Maximum (EM) algorithm (Dempster, Laird, and Rubin, 1977; Laird, Lange, and Stram, 1987), as well as analytical details for implementing a QR-decomposition approach to the problem. Wolfinger, Tobias, and Sall (1994) present the sweep-based algorithms that are implemented in PROC MIXED.

One advantage of using the Newton-Raphson algorithm is that the second derivative matrix of the objective function evaluated at the optima is available upon completion. Denoting this matrix $\bH $, the asymptotic theory of maximum likelihood (see Serfling 1980) shows that $2\bH ^{-1}$ is an asymptotic variance-covariance matrix of the estimated parameters of $\bG $ and $\bR $. Thus, tests and confidence intervals based on asymptotic normality can be obtained. However, these can be unreliable in small samples, especially for parameters such as variance components that have sampling distributions that tend to be skewed to the right.

If a residual variance $\sigma ^2$ is a part of your mixed model, it can usually be profiled out of the likelihood. This means solving analytically for the optimal $\sigma ^2$ and plugging this expression back into the likelihood formula (see Wolfinger, Tobias, and Sall 1994). This reduces the number of optimization parameters by one and can improve convergence properties. PROC MIXED profiles the residual variance out of the log likelihood whenever it appears reasonable to do so. This includes the case when $\mb {R}$ equals $\sigma ^2\mb {I} $ and when it has blocks with a compound symmetry, time series, or spatial structure. PROC MIXED does not profile the log likelihood when $\mb {R}$ has unstructured blocks, when you use the HOLD= or NOITER option in the PARMS statement, or when you use the NOPROFILE option in the PROC MIXED statement.

Instead of ML or REML, you can use the noniterative MIVQUE0 method to estimate $\mb {G}$ and $\mb {R}$ (Rao, 1972; LaMotte, 1973; Wolfinger, Tobias, and Sall, 1994). In fact, by default PROC MIXED uses MIVQUE0 estimates as starting values for the ML and REML procedures. For variance component models, another estimation method involves equating Type 1, 2, or 3 expected mean squares to their observed values and solving the resulting system. However, Swallow and Monahan (1984) present simulation evidence favoring REML and ML over MIVQUE0 and other method-of-moment estimators.

Estimating Fixed and Random Effects in the Mixed Model

ML, REML, MIVQUE0, or Type1–Type3 provide estimates of $\bG $ and $\bR $, which are denoted $\widehat{\bG }$ and $\widehat{\bR }$, respectively. To obtain estimates of $\bbeta $ and $\bgamma $, the standard method is to solve the mixed model equations (Henderson, 1984):

\[ \left[\begin{array}{lr} \bX ’\widehat{\bR }^{-1}\bX & \bX ’\widehat{\bR }^{-1}\bZ \\*\bZ ’\widehat{\bR }^{-1}\bX & \bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1} \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR }^{-1}\mb {y} \\ \bZ ’\widehat{\bR }^{-1}\mb {y} \end{array} \right] \]

The solutions can also be written as

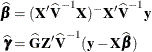
\begin{align*} \widehat{\bbeta } & = (\bX ’\widehat{\bV }^{-1}\bX )^{-} \bX ’\widehat{\bV }^{-1}\mb {y} \\ \widehat{\bgamma } & = \widehat{\bG }\bZ ’\widehat{\bV }^{-1} (\mb {y} - \bX \widehat{\bbeta }) \end{align*}

and have connections with empirical Bayes estimators (Laird and Ware, 1982; Carlin and Louis, 1996).

Note that the mixed model equations are extended normal equations and that the preceding expression assumes that $\widehat{\bG }$ is nonsingular. For the extreme case where the eigenvalues of $\widehat{\bG }$ are very large, $\widehat{\bG }^{-1}$ contributes very little to the equations and $\widehat{\bgamma }$ is close to what it would be if $\bgamma $ actually contained fixed-effects parameters. On the other hand, when the eigenvalues of $\widehat{\bG }$ are very small, $\widehat{\bG }^{-1}$ dominates the equations and $\widehat{\bgamma }$ is close to 0. For intermediate cases, $\widehat{\bG }^{-1}$ can be viewed as shrinking the fixed-effects estimates of $\bgamma $ toward 0 (Robinson, 1991).

If $\widehat{\bG }$ is singular, then the mixed model equations are modified (Henderson, 1984) as follows:

\[ \left[\begin{array}{lr} \bX ’\widehat{\bR } ^{-1}\bX & \bX ’\widehat{\bR } ^{-1} \bZ \widehat{\bG } \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bX & \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bZ \widehat{\bG } + \bG \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\btau } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR } ^{-1}\mb {y} \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\mb {y} \end{array} \right] \]

Denote the generalized inverses of the nonsingular $\widehat{\bG }$ and singular $\widehat{\bG }$ forms of the mixed model equations by $\bC $ and $\bM $, respectively. In the nonsingular case, the solution $\widehat{\bgamma }$ estimates the random effects directly, but in the singular case the estimates of random effects are achieved through a back-transformation $\widehat{\bgamma } = \widehat{\bG }\widehat{\btau }$ where $\widehat{\btau }$ is the solution to the modified mixed model equations. Similarly, while in the nonsingular case $\bC $ itself is the estimated covariance matrix for $(\widehat{\bbeta },\widehat{\bgamma })$, in the singular case the covariance estimate for $(\widehat{\bbeta },\widehat{\bG }\widehat{\btau })$ is given by $\bP \bM \bP $ where

\[ \bP = \left[\begin{array}{cc} \bI & \\ & \widehat{\bG } \end{array}\right] \]

An example of when the singular form of the equations is necessary is when a variance component estimate falls on the boundary constraint of 0.

Model Selection

The previous section on estimation assumes the specification of a mixed model in terms of $\mb {X}$, $\mb {Z}$, $\mb {G}$, and $\mb {R}$. Even though $\mb {X}$ and $\mb {Z}$ have known elements, their specific form and construction are flexible, and several possibilities can present themselves for a particular data set. Likewise, several different covariance structures for $\mb {G}$ and $\mb {R}$ might be reasonable.

Space does not permit a thorough discussion of model selection, but a few brief comments and references are in order. First, subject matter considerations and objectives are of great importance when selecting a model; see Diggle (1988) and Lindsey (1993).

Second, when the data themselves are looked to for guidance, many of the graphical methods and diagnostics appropriate for the general linear model extend to the mixed model setting as well (Christensen, Pearson, and Johnson, 1992).

Finally, a likelihood-based approach to the mixed model provides several statistical measures for model adequacy as well. The most common of these are the likelihood ratio test and Akaike’s and Schwarz’s criteria (Bozdogan, 1987; Wolfinger, 1993; Keselman et al., 1998, 1999).

Statistical Properties

If $\bG $ and $\bR $ are known, $\widehat{\bbeta }$ is the best linear unbiased estimator (BLUE) of $\bbeta $, and $\widehat{\bgamma }$ is the best linear unbiased predictor (BLUP) of $\bgamma $ (Searle, 1971; Harville, 1988, 1990; Robinson, 1991; McLean, Sanders, and Stroup, 1991). Here, “best” means minimum mean squared error. The covariance matrix of $(\widehat{\bbeta } - \bbeta ,\widehat{\bgamma } - \bgamma )$ is

\[ \mb {C} = \left[\begin{array}{cc} \mb {X}’\mb {R}^{-1}\mb {X} & \mb {X}’\mb {R}^{-1}\mb {Z} \\*\mb {Z}’\mb {R}^{-1}\mb {X} & \mb {Z}’\mb {R}^{-1}\mb {Z} + \mb {G}^{-1} \end{array}\right]^{-} \]

where $^-$ denotes a generalized inverse (see Searle 1971).

However, $\bG $ and $\bR $ are usually unknown and are estimated by using one of the aforementioned methods. These estimates, $\widehat{\bG }$ and $\widehat{\bR }$, are therefore simply substituted into the preceding expression to obtain

\[ \widehat{\mb {C}} = \left[\begin{array}{cc} \bX ’\widehat{\bR }^{-1}\bX & \bX ’\widehat{\bR }^{-1}\bZ \\*\bZ ’\widehat{\bR }^{-1}\bX & \bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1} \end{array}\right]^{-} \]

as the approximate variance-covariance matrix of $(\widehat{\bbeta } - \bbeta ,\widehat{\bgamma } - \bgamma $). In this case, the BLUE and BLUP acronyms no longer apply, but the word empirical is often added to indicate such an approximation. The appropriate acronyms thus become EBLUE and EBLUP.

McLean and Sanders (1988) show that $\widehat{\bC }$ can also be written as

\[ \widehat{\bC } = \left[\begin{array}{cc} \widehat{\bC }_{11} & \widehat{\bC }_{21}’ \\ \widehat{\bC }_{21} & \widehat{\bC }_{22} \end{array}\right] \]

where

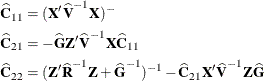
\begin{align*} \widehat{\bC }_{11} & = (\bX ’\widehat{\bV }^{-1}\bX )^{-} \\ \widehat{\bC }_{21} & = -\widehat{\bG }\bZ ’\widehat{\bV }^{-1}\bX \widehat{\bC }_{11} \\ \widehat{\bC }_{22} & = (\bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1})^{-1} - \widehat{\bC }_{21}\bX ’\widehat{\bV }^{-1}\bZ \widehat{\bG } \end{align*}

Note that $\widehat{\bC }_{11}$ is the familiar estimated generalized least squares formula for the variance-covariance matrix of $\widehat{\bbeta }$.

As a cautionary note, $\widehat{\bC }$ tends to underestimate the true sampling variability of ($\widehat{\bbeta }$ $\widehat{\bgamma }$) because no account is made for the uncertainty in estimating $\bG $ and $\bR $. Although inflation factors have been proposed (Kackar and Harville, 1984; Kass and Steffey, 1989; Prasad and Rao, 1990), they tend to be small for data sets that are fairly well balanced. PROC MIXED does not compute any inflation factors by default, but rather accounts for the downward bias by using the approximate t and F statistics described subsequently. The DDFM=KENWARDROGER option in the MODEL statement prompts PROC MIXED to compute a specific inflation factor along with Satterthwaite-based degrees of freedom.

Inference and Test Statistics

For inferences concerning the covariance parameters in your model, you can use likelihood-based statistics. One common likelihood-based statistic is the Wald Z, which is computed as the parameter estimate divided by its asymptotic standard error. The asymptotic standard errors are computed from the inverse of the second derivative matrix of the likelihood with respect to each of the covariance parameters. The Wald Z is valid for large samples, but it can be unreliable for small data sets and for parameters such as variance components, which are known to have a skewed or bounded sampling distribution.

A better alternative is the likelihood ratio $\chi ^2$ statistic. This statistic compares two covariance models, one a special case of the other. To compute it, you must run PROC MIXED twice, once for each of the two models, and then subtract the corresponding values of –2 times the log likelihoods. You can use either ML or REML to construct this statistic, which tests whether the full model is necessary beyond the reduced model.

As long as the reduced model does not occur on the boundary of the covariance parameter space, the $\chi ^2$ statistic computed in this fashion has a large-sample $\chi ^2$ distribution that is $\chi ^2$ with degrees of freedom equal to the difference in the number of covariance parameters between the two models. If the reduced model does occur on the boundary of the covariance parameter space, the asymptotic distribution becomes a mixture of $\chi ^2$ distributions (Self and Liang, 1987). A common example of this is when you are testing that a variance component equals its lower boundary constraint of 0.

A final possibility for obtaining inferences concerning the covariance parameters is to simulate or resample data from your model and construct empirical sampling distributions of the parameters. The SAS macro language and the ODS system are useful tools in this regard.

F and t Tests for Fixed- and Random-Effects Parameters

For inferences concerning the fixed- and random-effects parameters in the mixed model, consider estimable linear combinations of the following form:

\[ \bL \left[\begin{array}{c} \bbeta \\ \bgamma \end{array} \right] \]

The estimability requirement (Searle, 1971) applies only to the $\bbeta $ portion of $\bL $, because any linear combination of $\bgamma $ is estimable. Such a formulation in terms of a general $\bL $ matrix encompasses a wide variety of common inferential procedures such as those employed with Type 1–Type 3 tests and LS-means. The CONTRAST and ESTIMATE statements in PROC MIXED enable you to specify your own $\bL $ matrices. Typically, inference on fixed effects is the focus, and, in this case, the $\bgamma $ portion of $\bL $ is assumed to contain all 0s.

Statistical inferences are obtained by testing the hypothesis

\[ H: \bL \left[\begin{array}{c} \bbeta \\ \bgamma \end{array} \right] = 0 \]

or by constructing point and interval estimates.

When $\bL $ consists of a single row, a general t statistic can be constructed as follows (see McLean and Sanders 1988; Stroup 1989a):

\[ t = \frac{\bL \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right]}{\sqrt {\bL \widehat{\bC }\mb {L}’}} \]

Under the assumed normality of $\bgamma $ and $\bepsilon $, t has an exact t distribution only for data exhibiting certain types of balance and for some special unbalanced cases. In general, t is only approximately t-distributed, and its degrees of freedom must be estimated. See the DDFM= option for a description of the various degrees-of-freedom methods available in PROC MIXED.

With $\widehat{\nu }$ being the approximate degrees of freedom, the associated confidence interval is

\[ \mb {L} \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right] \pm t_{\widehat{\nu },\alpha /2} \sqrt {\mb {L}\widehat{\bC }\bL ’} \]

where $t_{\widehat{\nu },\alpha /2}$ is the $(1 - \alpha /2)100$ percentile of the $t_{\widehat{\nu }}$ distribution.

When the rank of $\bL $ is greater than 1, PROC MIXED constructs the following general F statistic:

\[ F = \frac{ \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right]\bL (\bL \widehat{\bC } \bL )^{-1} \bL \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right]}{r} \]

where $r = \mr {rank}(\bL \widehat{\bC }\bL ’)$. Analogous to t, F in general has an approximate F distribution with r numerator degrees of freedom and $\widehat{\nu }$ denominator degrees of freedom.

The t and F statistics enable you to make inferences about your fixed effects, which account for the variance-covariance model you select. An alternative is the $\chi ^2$ statistic associated with the likelihood ratio test. This statistic compares two fixed-effects models, one a special case of the other. It is computed just as when comparing different covariance models, although you should use ML and not REML here because the penalty term associated with restricted likelihoods depends upon the fixed-effects specification.

F Tests With the ANOVAF Option

The ANOVAF option computes F tests by the following method in models with REPEATED statement and without RANDOM statement. Let $\bL $ denote the matrix of estimable functions for the hypothesis $H\colon \bL \bbeta = \mb {0}$, where $\bbeta $ are the fixed-effects parameters. Let $\bM = \bL ’(\bL \bL ’)^{-}\bL $, and suppose that $\widehat{\bC }$ denotes the estimated variance-covariance matrix of $\widehat{\bbeta }$ (see the section Statistical Properties for the construction of $\widehat{\bC }$).

The ANOVAF F statistics are computed as

\[ F_ A = \widehat{\bbeta }’\bL ’ \left(\bL \bL ’\right)^{-1} \bL \widehat{\bbeta } \Big/ t_1 = \widehat{\bbeta }’\mb {M} \widehat{\bbeta } \Big/ t_1 \\ \]

Notice that this is a modification of the usual F statistic where $(\bL \widehat{\bC }\bL ’)^{-1}$ is replaced with $(\bL \bL ’)^{-1}$ and $\mr {rank}(\bL )$ is replaced with $t_1 = \mr {trace}(\bM \widehat{\bC })$; see, for example, Brunner, Domhof, and Langer (2002, Sec. 5.4). The p-values for this statistic are computed from either an $F_{{\nu _1},{\nu _2}}$ or an $F_{{\nu _1},\infty }$ distribution. The respective degrees of freedom are determined by the MIXED procedure as follows:

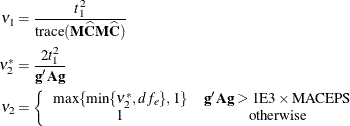
\begin{align*} \nu _1 & = \frac{t_1^2}{\mr {trace}(\bM \widehat{\bC }\bM \widehat{\bC })} \\ \nu _2^* & = \frac{2t_1^2}{\mb {g}\bA \mb {g}} \\ \nu _2 & = \left\{ \begin{array}{cc} \max \{ \min \{ \nu _2^*,df_ e\} ,1\} & \mb {g}’\mb {A}\mb {g} > 1\mr {E}3\times \mr {MACEPS} \\ 1 & \mr {otherwise} \end{array} \right. \end{align*}

The term $\mb {g}’\bA \mb {g}$ in the term $\nu _2^*$ for the denominator degrees of freedom is based on approximating $\mr {Var}[\mr {trace}(\bM \widehat{\bC })]$ based on a first-order Taylor series about the true covariance parameters. This generalizes results in the appendix of Brunner, Dette, and Munk (1997) to a broader class of models. The vector $\mb {g} = [g_1,\cdots ,g_ q]$ contains the partial derivatives

\[ \mr {trace}\left( \bL ’\left(\bL \bL ’\right)^{-1}\bL \frac{\partial \widehat{\bC }}{\partial \theta _ i} \right) \]

and $\bA $ is the asymptotic variance-covariance matrix of the covariance parameter estimates (ASYCOV option).

PROC MIXED reports $\nu _1$ and $\nu _2$ as “NumDF” and “DenDF” under the “ANOVA F” heading in the output. The corresponding p-values are denoted as “Pr > F(DDF)” for $F_{{\nu _1},{\nu _2}}$ and “Pr > F(infty)” for $F_{{\nu _1},\infty }$, respectively.

P-values computed with the ANOVAF option can be identical to the nonparametric tests in Akritas, Arnold, and Brunner (1997) and in Brunner, Domhof, and Langer (2002), provided that the response data consist of properly created (and sorted) ranks and that the covariance parameters are estimated by MIVQUE0 in models with REPEATED statement and properly chosen SUBJECT= and/or GROUP= effects.

If you model an unstructured covariance matrix in a longitudinal model with one or more repeated factors, the ANOVAF results are identical to a multivariate MANOVA where degrees of freedom are corrected with the Greenhouse-Geisser adjustment (Greenhouse and Geisser, 1959). For example, suppose that factor A has 2 levels and factor B has 4 levels. The following two sets of statements produce the same p-values: 

proc mixed data=Mydata anovaf method=mivque0;
   class id A B;
   model score = A | B / chisq;
   repeated / type=un subject=id;
   ods select Tests3;
run;

proc transpose data=MyData out=tdata;
   by id;
   var score;
run;
proc glm data=tdata;
   model col: = / nouni;
   repeated A 2, B 4;
   ods output ModelANOVA=maov epsilons=eps;
run;
proc transpose data=eps(where=(substr(statistic,1,3)='Gre')) out=teps;
   var cvalue1;
run;

data aov; set maov;
   if (_n_ = 1) then merge teps;
   if (Source='A') then do;
      pFddf = ProbF;
      pFinf = 1 - probchi(df*Fvalue,df);
      output;
   end; else if (Source='B') then do;
      pFddf = ProbFGG;
      pFinf = 1 - probchi(df*col1*Fvalue,df*col1);
      output;
   end; else if (Source='A*B') then do;
      pfddF = ProbFGG;
      pFinf = 1 - probchi(df*col2*Fvalue,df*col2);
      output;
   end;
run;
proc print data=aov label noobs;
   label Source = 'Effect'
         df     = 'NumDF'
         Fvalue = 'Value'
         pFddf  = 'Pr > F(DDF)'
         pFinf  = 'Pr > F(infty)';
   var Source df Fvalue pFddf pFinf;
   format pF: pvalue6.;
run;

The PROC GLM code produces p-values that correspond to the ANOVAF p-values shown as Pr > F(DDF) in the MIXED output. The subsequent DATA step computes the p-values that correspond to Pr > F(infty) in the PROC MIXED output.

Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.