The LOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model - References
The likelihood equation for a logistic regression model does not always have a finite solution. Sometimes there is a nonunique maximum on the boundary of the parameter space, at infinity. The existence, finiteness, and uniqueness of maximum likelihood estimates for the logistic regression model depend on the patterns of data points in the observation space (Albert and Anderson, 1984; Santner and Duffy, 1986). Existence checks are not performed for conditional logistic regression.
Consider a binary response model. Let ![]() be the response of the jth subject, and let
be the response of the jth subject, and let ![]() be the vector of explanatory variables (including the constant 1 associated with the intercept). There are three mutually
exclusive and exhaustive types of data configurations: complete separation, quasi-complete separation, and overlap.
be the vector of explanatory variables (including the constant 1 associated with the intercept). There are three mutually
exclusive and exhaustive types of data configurations: complete separation, quasi-complete separation, and overlap.
- Complete Separation
-
There is a complete separation of data points if there exists a vector
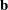 that correctly allocates all observations to their response groups; that is,
that correctly allocates all observations to their response groups; that is,
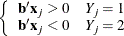
This configuration gives nonunique infinite estimates. If the iterative process of maximizing the likelihood function is allowed to continue, the log likelihood diminishes to zero, and the dispersion matrix becomes unbounded.
- Quasi-complete Separation
-
The data are not completely separable, but there is a vector
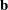 such that
such that
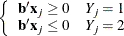
and equality holds for at least one subject in each response group. This configuration also yields nonunique infinite estimates. If the iterative process of maximizing the likelihood function is allowed to continue, the dispersion matrix becomes unbounded and the log likelihood diminishes to a nonzero constant.
- Overlap
-
If neither complete nor quasi-complete separation exists in the sample points, there is an overlap of sample points. In this configuration, the maximum likelihood estimates exist and are unique.
Complete separation and quasi-complete separation are problems typically encountered with small data sets. Although complete separation can occur with any type of data, quasi-complete separation is not likely with truly continuous explanatory variables.
The LOGISTIC procedure uses a simple empirical approach to recognize the data configurations that lead to infinite parameter
estimates. The basis of this approach is that any convergence method of maximizing the log likelihood must yield a solution
giving complete separation, if such a solution exists. In maximizing the log likelihood, there is no checking for complete
or quasi-complete separation if convergence is attained in eight or fewer iterations. Subsequent to the eighth iteration,
the probability of the observed response is computed for each observation. If the predicted response equals the observed response
for every observation, there is a complete separation of data points and the iteration process is stopped. If the complete
separation of data has not been determined and an observation is identified to have an extremely large probability (![]() 0.95) of predicting the observed response, there are two possible situations. First, there is overlap in the data set, and
the observation is an atypical observation of its own group. The iterative process, if allowed to continue, will stop when
a maximum is reached. Second, there is quasi-complete separation in the data set, and the asymptotic dispersion matrix is
unbounded. If any of the diagonal elements of the dispersion matrix for the standardized observations vectors (all explanatory
variables standardized to zero mean and unit variance) exceeds 5000, quasi-complete separation is declared and the iterative
process is stopped. If either complete separation or quasi-complete separation is detected, a warning message is displayed
in the procedure output.
0.95) of predicting the observed response, there are two possible situations. First, there is overlap in the data set, and
the observation is an atypical observation of its own group. The iterative process, if allowed to continue, will stop when
a maximum is reached. Second, there is quasi-complete separation in the data set, and the asymptotic dispersion matrix is
unbounded. If any of the diagonal elements of the dispersion matrix for the standardized observations vectors (all explanatory
variables standardized to zero mean and unit variance) exceeds 5000, quasi-complete separation is declared and the iterative
process is stopped. If either complete separation or quasi-complete separation is detected, a warning message is displayed
in the procedure output.
Checking for quasi-complete separation is less foolproof than checking for complete separation. The NOCHECK option in the MODEL statement turns off the process of checking for infinite parameter estimates. In cases of complete or quasi-complete separation, turning off the checking process typically results in the procedure failing to converge. The presence of a WEIGHT statement also turns off the checking process.
To address the separation issue, you can change your model, specify the FIRTH option to use Firth’s penalized likelihood method, or for small data sets specify an EXACT statement to perform an exact logistic regression.