-
ALPHA=number-list
-
specifies the level of significance of each test. The default is 0.05, corresponding to the usual 0.05  100% = 5% level of significance. Note that this is a test-wise significance level with the same value for all tests, not
incorporating any corrections for multiple testing. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
100% = 5% level of significance. Note that this is a test-wise significance level with the same value for all tests, not
incorporating any corrections for multiple testing. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
-
CORRMAT=name-list
-
specifies the correlation matrix of the dependent variables in a multivariate model, by using labels that are specified in
the MATRIX= option. The corresponding matrices that are defined in the MATRIX= option must have either a lower triangular form that includes the diagonal of 1’s or a linear exponent autoregressive (LEAR) correlation structure. The matrix must be positive definite.
You can use the CORRMAT= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements. For information about specifying the name-list, see the section Specifying Value Lists in the POWER Statement.
-
CORRS=name-list
-
specifies the correlations among the dependent variables in a multivariate model, by using labels that are specified in the
MATRIX= option. The corresponding matrices that are defined in the MATRIX= option must have either a lower triangular form that excludes the diagonal of 1’s or a LEAR correlation structure. The matrix must be positive definite. You can use the CORRS= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements. For information about specifying the name-list, see the section Specifying Value Lists in the POWER Statement.
-
COVMAT=name-list
-
specifies the covariance matrix of the dependent variables in a multivariate model, by using labels that are specified in
the MATRIX= option. The corresponding matrices that are defined in the MATRIX= option must have a lower triangular form that includes the diagonal of error variances. The matrix must be positive definite.
You can use the COVMAT= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements. For information about specifying the name-list, see the section Specifying Value Lists in the POWER Statement.
-
CORRXY=number-list
-
specifies the multiple correlation (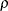 ) between all covariates and the response for a univariate model. The error standard deviation that is given by the STDDEV= option is consequently reduced by multiplying it by a factor of
) between all covariates and the response for a univariate model. The error standard deviation that is given by the STDDEV= option is consequently reduced by multiplying it by a factor of 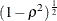 , provided that the number of covariates (as determined by the NCOVARIATES= option) is greater than 0. You cannot use the CORRXY= and PROPVARREDUCTION= options simultaneously. You cannot use the CORRXY= option when you have a multivariate model—that is, in the presence of a MANOVA or REPEATED statement. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
, provided that the number of covariates (as determined by the NCOVARIATES= option) is greater than 0. You cannot use the CORRXY= and PROPVARREDUCTION= options simultaneously. You cannot use the CORRXY= option when you have a multivariate model—that is, in the presence of a MANOVA or REPEATED statement. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
-
DEPENDENT
-
specifies the location of the Dependent column (for a univariate model) or the Transformation column (for a multivariate model)
in the output when you specify the OUTPUTORDER=REVERSE option or OUTPUTORDER=SYNTAX option, according to its relative position in the POWER statement.
-
EFFECTS <= <( effect …effect ) >>
-
specifies the model effects to include in the power analysis. By default, or if the EFFECTS keyword is specified without the
equal sign (=), all model effects are included. Specify EFFECTS=() to exclude all model effect tests from the power analysis. You can include main effects and interactions by using the
effects notation of PROC GLM; see the section Specification of Effects in Chapter 44: The GLM Procedure for further details. The MODEL statement must appear before the POWER statement if the EFFECTS option is used.
-
MATRIX('label')=matrix-specification
-
defines a matrix or vector that you can use along with the CORRMAT=, CORRS=, COVMAT=, and SQRTVAR= options when you have a multivariate model.
The matrix-specification can have one of the following three forms:
1. Raw values
specifies the values of a matrix or vector in one of the following forms:
-
a matrix in lower triangular form, for use with the CORRMAT= or COVMAT= option
-
a matrix in strictly lower triangular form, for use with the CORRS= option
-
a vector, for use with the SQRTVAR= option
A matrix in lower triangular form contains the diagonal the and values below it. For example, you can represent a  correlation matrix for use with the CORRMAT= option as follows:
correlation matrix for use with the CORRMAT= option as follows:
MATRIX ('MyCorrMat') = ( 1
0.5 1
0.2 0.5 1)
You can represent the same correlation matrix in strictly lower triangular form for use with the CORRS= option as follows:
MATRIX ('MyCorrs') = (0.5
0.2 0.5)
An example of a vector for use with the SQRTVAR= option is as follows:
MATRIX ('MySqrtVar') = (3.2 4.5 3.7)
2. Linear exponent autoregressive (LEAR) correlation structure
LEAR (base-corr, corr-decay <, nlevels <, level-values>> )
specifies a LEAR correlation structure for use with the CORRMAT= or CORRS= option. The LEAR structure is useful for characterizing exponentially decaying within-subject correlation that decays at
a rate slower or faster than AR(1). Special cases include compound symmetry, first-order autoregressive (AR(1)), and first-order
moving average correlation structures.
The LEAR correlation structure is related to the spatial covariance structures in PROC MIXED and is discussed in Simpson et al.
(2010).
The base-corr (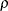 ) is the correlation between variables whose level-values are one unit apart, and it must satisfy
) is the correlation between variables whose level-values are one unit apart, and it must satisfy 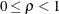 . The corr-decay (
. The corr-decay (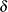 ) is the correlation decay rate, which must be nonnegative. The default number of levels, nlevels (
) is the correlation decay rate, which must be nonnegative. The default number of levels, nlevels ( ), is the number of dependent variables. The default values for the
), is the number of dependent variables. The default values for the  level-values, denoted
level-values, denoted 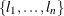 , are
, are 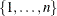 . Let
. Let 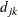 denote the distance between levels
denote the distance between levels 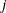 and
and 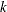 ,
, 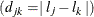 . Let
. Let 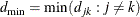 and
and 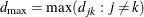 . The
. The 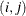 th element of the correlation matrix according to the LEAR model is defined as
th element of the correlation matrix according to the LEAR model is defined as
Compound symmetry is the special case 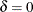 . AR(1) is the special case
. AR(1) is the special case 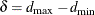 . As
. As 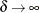 , the model approaches the first-order moving average model.
, the model approaches the first-order moving average model.
3. Kronecker product
'matrix-name' @ 'matrix-name' <@ …@ 'matrix-name'>
specifies a direct (Kronecker) product of two or more matrices for use with the CORRMAT=, CORRS=, or COVMAT= option. This form is useful when you have more than one type of distinction among dependent variables. For example, suppose
you have a three-level repeated measurement factor with correlation that is 0.4 for neighboring measurements and that decays
slightly more slowly than AR(1) across more distant measurements. You also have four clusters that you believe satisfy compound
symmetry with a correlation of 0.3. Your level values are the same as the default for the LEAR model. You can specify this
correlation structure as follows:
MATRIX ('RepMeasures') = LEAR (0.4, 1.5, 3)
MATRIX ('Clusters') = LEAR (0.3, 0, 4)
MATRIX ('FullCorr') = 'RepMeasures' @ 'Clusters'
CORRMAT = 'FullCorr'
You can use the MATRIX option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements.
-
METHOD=MULLERPETERSON | MP
METHOD=OBRIENSHIEH | OS
-
specifies the power computation method for the multivariate tests (MTEST=HLT, MTEST=PT, and MTEST=WILKS). METHOD=OBRIENSHIEH (the default) is based on O’Brien and Shieh (1992), and METHOD=MULLERPETERSON is based on Muller and Peterson (1984). For information about the associated power and sample size computational methods and formulas, see the section Multivariate Tests.
If the dependent variable transformation consists of a single contrast (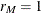 ), then the two methods are identical and compute exact power. If
), then the two methods are identical and compute exact power. If 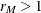 but the model effect or between-subject contrast has only one degree of freedom (
but the model effect or between-subject contrast has only one degree of freedom (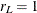 ), then METHOD=OBRIENSHIEH computes exact results and METHOD=MULLERPETERSON computes approximate results. If
), then METHOD=OBRIENSHIEH computes exact results and METHOD=MULLERPETERSON computes approximate results. If 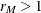 and
and 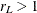 , then both methods compute approximate results.
, then both methods compute approximate results.
You can use the METHOD= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements.
-
MTEST=test-list
-
specifies the form of the 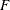 test for a multivariate model. Seven keywords are available, as discussed in the following paragraphs: BOX, GG, HF, HLT,
PT, UNCORR, and WILKS. For information about specifying the keyword-list, see the section Specifying Value Lists in the POWER Statement.
test for a multivariate model. Seven keywords are available, as discussed in the following paragraphs: BOX, GG, HF, HLT,
PT, UNCORR, and WILKS. For information about specifying the keyword-list, see the section Specifying Value Lists in the POWER Statement.
Three of these tests are multivariate, corresponding to the default MSTAT=FAPPROX option in the MANOVA and REPEATED statements
in PROC GLM:
-
MTEST=HLT (the default) is the Hotelling-Lawley trace
-
MTEST=PT is Pillai’s trace
-
MTEST=WILKS is Wilks’ lambda
For more information about these multivariate tests, see the section Multivariate Tests in Chapter 4: Introduction to Regression Procedures. For information about the associated power and sample size computational methods and formulas, see the section Multivariate Tests.
The other four tests are univariate, corresponding to the univariate approach to repeated measures in the REPEATED statement
in PROC GLM:
For more information about these univariate tests, see the section Hypothesis Testing in Repeated Measures Analysis in Chapter 44: The GLM Procedure. For information about the associated power and sample size computational methods and formulas, see the section Univariate Tests.
These tests are all of the form 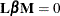 , where
, where  is a between-subject contrast,
is a between-subject contrast, 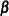 is the matrix of model parameters, and
is the matrix of model parameters, and 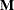 is a within-subject contrast.
is a within-subject contrast.
You can use the MTEST= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements.
-
NCOVARIATES=number-list
NCOVARIATE=number-list
NCOVS=number-list
NCOV=number-list
-
specifies the number of additional degrees of freedom to accommodate covariate effects—both class and continuous—not listed
in the MODEL statement, for a univariate model. The error degrees of freedom are consequently reduced by the value of the NCOVARIATES= option, and the error standard deviation (whose unadjusted value is provided with the STDDEV= option) is reduced according to the value of the CORRXY= or PROPVARREDUCTION= option. You cannot use the NCOVARIATES= option when you have a multivariate model—that is, in the presence of a MANOVA or REPEATED statement. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
-
NFRACTIONAL
NFRAC
-
enables fractional input and output for sample sizes. See the section Sample Size Adjustment Options for information about the ramifications of the presence (and absence) of the NFRACTIONAL option.
-
NTOTAL=number-list
-
specifies the sample size or requests a solution for the sample size with a missing value (NTOTAL=.). The term “sample size” here refers to the number of independent sampling units. Values for the sample size for a univariate model must be no smaller
than the model degrees of freedom (counting the covariates if present). The minimum required sample size for a multivariate
model depends on the analysis and computational method; for more information, see the section Contrasts in Fixed-Effect Multivariate Models. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
-
OUTPUTORDER=INTERNAL | REVERSE | SYNTAX
-
controls how the input and default analysis parameters are ordered in the output. OUTPUTORDER=INTERNAL (the default) arranges the parameters in the output according to the following order of their corresponding options:
The OUTPUTORDER=SYNTAX option arranges the parameters in the output in the same order in which their corresponding options are specified in
the POWER statement. The OUTPUTORDER=REVERSE option arranges the parameters in the output in the reverse of the order in which their corresponding options are
specified in the POWER statement.
-
POWER=number-list
-
specifies the desired power of each test or requests a solution for the power with a missing value (POWER=.). The power is expressed as a probability (for example, 0.9) rather than a percentage. Note that this is a test-wise power
with the same value for all tests, without any correction for multiple testing. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
-
PROPVARREDUCTION=number-list
PVRED=number-list
-
specifies the proportional reduction (r) in total R square incurred by the covariates—in other words, the amount of additional variation explained by the covariates—for
a univariate model. The error standard deviation that is given by the STDDEV= option is consequently reduced by multiplying it by a factor of 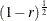 , provided that the number of covariates (as determined by the NCOVARIATES= option) is greater than 0. You cannot use the PROPVARREDUCTION= and CORRXY= options simultaneously. You cannot use the PROPVARREDUCTION= option when you have a multivariate model—that is, in the presence of a MANOVA or REPEATED statement. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
, provided that the number of covariates (as determined by the NCOVARIATES= option) is greater than 0. You cannot use the PROPVARREDUCTION= and CORRXY= options simultaneously. You cannot use the PROPVARREDUCTION= option when you have a multivariate model—that is, in the presence of a MANOVA or REPEATED statement. For information about specifying the number-list, see the section Specifying Value Lists in the POWER Statement.
-
SQRTVAR=name-list
-
specifies the vector of standard deviations—that is, the square roots of the variances—of the dependent variables in a multivariate
model, by using labels that are specified using the MATRIX= option. The standard deviation values must be positive. You can use the SQRTVAR= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements. For information about specifying the name-list, see the section Specifying Value Lists in the POWER Statement.
-
STDDEV=number-list
-
specifies the error standard deviation, or root MSE. For a multivariate model, each value in the number-list is taken to be a common value for all dependent variables. If covariates are specified by using the NCOVARIATES= option, then the STDDEV= option denotes the error standard deviation before accounting for these covariates. For information about specifying the
number-list, see the section Specifying Value Lists in the POWER Statement.
-
UEPSDEF=unbiased-epsilon-definition
-
specifies the type of adjustment for MTEST=HF. The default is UEPSDEF=HFL, corresponding to the corrected form of the Huynh-Feldt adjustment (Huynh and Feldt; 1976; Lecoutre; 1991). Other alternatives are UEPSDEF=HF; the uncorrected Huynh-Feldt adjustment; and UEPSDEF=CM, the adjustment of Chi et al. (2012). For more information about these adjustments, see the section Hypothesis Testing in Repeated Measures Analysis in Chapter 44: The GLM Procedure. You can use the UEPSDEF= option only when you have a multivariate model—that is, in the presence of one or more MANOVA or REPEATED statements. For information about the associated power and sample size computational methods and formulas, see the section
Univariate Tests.
![]() tests that are specified in the MTEST= option, for each effect in the model that is defined by the MODEL statement, and for the contrasts that are defined by all CONTRAST, MANOVA, and REPEATED statements. The POWER statement must appear after the MODEL statement if the EFFECTS= option is used in the POWER statement.
tests that are specified in the MTEST= option, for each effect in the model that is defined by the MODEL statement, and for the contrasts that are defined by all CONTRAST, MANOVA, and REPEATED statements. The POWER statement must appear after the MODEL statement if the EFFECTS= option is used in the POWER statement.

![\begin{equation*} \rho _{jk} = \begin{cases} 1 & \text {if $j=k$}\\ \rho ^{d_\mr {min} + \delta [(d_{jk}-d_\mr {min})/(d_\mr {max}-d_\mr {min})]} & \text {if $j \ne k$ and $d_\mr {min} \ne d_\mr {max}$}\\ \rho & \text {if $j \ne k$ and $d_\mr {min}=d_\mr {max}$} \end{cases}\end{equation*}](images/statug_glmpower0039.png)