The BCHOICE Procedure (Experimental)
PREDDIST <'label'> OUTPRED=SAS-data-set <COVARIATES=SAS-data-set> ;
The PREDDIST statement creates a new SAS data set that contains random samples from the posterior predictive distribution
of the choice probabilities. The posterior predictive distribution is the distribution of unobserved observations (prediction)
conditional on the observed data. Let ![]() be the observed data,
be the observed data, ![]() be the covariates,
be the covariates, ![]() be the parameter, and
be the parameter, and ![]() be the unobserved data. The posterior predictive distribution is defined as follows:
be the unobserved data. The posterior predictive distribution is defined as follows:
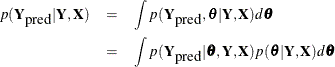
Assuming that the observed and unobserved data are conditionally independent given ![]() , the posterior predictive distribution can be further simplified as follows:
, the posterior predictive distribution can be further simplified as follows:
The posterior predictive distribution is an integral of the likelihood function ![]() with respect to the posterior distribution
with respect to the posterior distribution ![]() . The PREDDIST statement generates samples from a posterior predictive distribution based on draws from the posterior distribution
of
. The PREDDIST statement generates samples from a posterior predictive distribution based on draws from the posterior distribution
of ![]() .
.
You can specify the following options:
