Computational Methods and Formulas
Previous Page|Next Page

The POWER Procedure

Analyses in the TWOSAMPLEMEANS Statement

Two-Sample t Test Assuming Equal Variances (TEST=DIFF)

The hypotheses for the two-sample t test are

$\displaystyle H_{0}\colon $
$\displaystyle \mu _\mr {diff}=\mu _0 $
$\displaystyle H_{1}\colon $
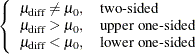$\displaystyle \left\{ \begin{array}{ll} \mu _\mr {diff} \ne \mu _0, & \mbox{two-sided} \\ \mu _\mr {diff} > \mu _0, & \mbox{upper one-sided} \\ \mu _\mr {diff} < \mu _0, & \mbox{lower one-sided} \\ \end{array} \right. $

The test assumes normally distributed data and common standard deviation per group, and it requires $N \ge 3$, $n_1 \ge 1$, and $n_2 \ge 1$. The test statistics are

$\displaystyle t $
$\displaystyle = N^\frac {1}{2} (w_1 w_2)^\frac {1}{2} \left( \frac{\bar{x}_2 - \bar{x}_1 - \mu _0}{s_ p} \right) \quad \thicksim \; \; t(N-2, \delta ) $
$\displaystyle t^2 $
$\displaystyle \thicksim F(1, N-2, \delta ^2) $

where $\bar{x}_1$ and $\bar{x}_2$ are the sample means and $s_ p$ is the pooled standard deviation, and

\[ \delta = N^\frac {1}{2} (w_1 w_2)^\frac {1}{2} \left( \frac{\mu _\mr {diff}-\mu _0}{\sigma } \right) \]

The test is

\[ \mbox{Reject} \quad H_0 \quad \mbox{if} \left\{ \begin{array}{ll} t^2 \ge F_{1-\alpha }(1, N-2), & \mbox{two-sided} \\ t \ge t_{1-\alpha }(N-2), & \mbox{upper one-sided} \\ t \le t_{\alpha }(N-2), & \mbox{lower one-sided} \\ \end{array} \right. \]

Exact power computations for t tests are given in O’Brien and Muller (1993, Section 8.2.1):

$\displaystyle \mr {power} $
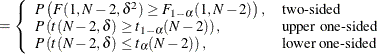$\displaystyle = \left\{ \begin{array}{ll} P\left(F(1, N-2, \delta ^2) \ge F_{1-\alpha }(1, N-2)\right), & \mbox{two-sided} \\ P\left(t(N-2, \delta ) \ge t_{1-\alpha }(N-2)\right), & \mbox{upper one-sided} \\ P\left(t(N-2, \delta ) \le t_{\alpha }(N-2)\right), & \mbox{lower one-sided} \\ \end{array} \right. $

Solutions for N, $n_1$, $n_2$, $\alpha $, and $\delta $ are obtained by numerically inverting the power equation. Closed-form solutions for other parameters, in terms of $\delta $, are as follows:

$\displaystyle \mu _\mr {diff} $
$\displaystyle = \delta \sigma (N w_1 w_2)^{-\frac{1}{2}} + \mu _0 $
$\displaystyle \mu _1 $
$\displaystyle = \delta \sigma (N w_1 w_2)^{-\frac{1}{2}} + \mu _0 - \mu _2 $
$\displaystyle \mu _2 $
$\displaystyle = \delta \sigma (N w_1 w_2)^{-\frac{1}{2}} + \mu _0 - \mu _1 $
$\displaystyle \sigma $
$\displaystyle = \left\{ \begin{array}{ll} \delta ^{-1} (N w_1 w_2)^\frac {1}{2} (\mu _\mr {diff} - \mu _0), & |\delta | > 0 \\ \mbox{undefined}, & \mbox{otherwise} \\ \end{array} \right. $
$\displaystyle w_1 $
$\displaystyle = \left\{ \begin{array}{ll} \frac{1}{2} \pm \frac{1}{2} \left[ 1 - \frac{4 \delta ^2 \sigma ^2}{N(\mu _\mr {diff} - \mu _0)^2} \right]^\frac {1}{2}, & 0 < |\delta | \le \frac{1}{2}N^\frac {1}{2} \frac{|\mu _\mr {diff} - \mu _0|}{\sigma } \\ \mbox{undefined}, & \mbox{otherwise} \\ \end{array} \right. $
$\displaystyle w_2 $
$\displaystyle = \left\{ \begin{array}{ll} \frac{1}{2} \pm \frac{1}{2} \left[ 1 - \frac{4 \delta ^2 \sigma ^2}{N(\mu _\mr {diff} - \mu _0)^2} \right]^\frac {1}{2}, & 0 < |\delta | \le \frac{1}{2}N^\frac {1}{2} \frac{|\mu _\mr {diff} - \mu _0|}{\sigma } \\ \mbox{undefined}, & \mbox{otherwise} \\ \end{array} \right. $

Finally, here is a derivation of the solution for $w_1$:

Solve the $\delta $ equation for $w_1$ (which requires the quadratic formula). Then determine the range of $\delta $ given $w_1$:

$\displaystyle \min _{w_1} (\delta ) $
$\displaystyle = \left\{ \begin{array}{ll} 0, & \mbox{when} \quad w_1 = 0 \quad \mbox{or} \quad 1, \quad \mbox{if} \quad (\mu _\mr {diff} - \mu _0) \ge 0 \\ \frac{1}{2}N^\frac {1}{2} \frac{(\mu _\mr {diff} - \mu _0)}{\sigma }, & \mbox{when} \quad w_1 = \frac{1}{2}, \quad \mbox{if} \quad (\mu _\mr {diff} - \mu _0) < 0 \\ \end{array} \right. $
$\displaystyle \max _{w_1} (\delta ) $
$\displaystyle = \left\{ \begin{array}{ll} 0, & \mbox{when} \quad w_1 = 0 \quad \mbox{or} \quad 1, \quad \mbox{if} \quad (\mu _\mr {diff} - \mu _0) < 0 \\ \frac{1}{2}N^\frac {1}{2} \frac{(\mu _\mr {diff} - \mu _0)}{\sigma }, & \mbox{when} \quad w_1 = \frac{1}{2}, \quad \mbox{if} \quad (\mu _\mr {diff} - \mu _0) \ge 0 \\ \end{array} \right. $

This implies

\[ |\delta | \le \frac{1}{2}N^\frac {1}{2} \frac{|\mu _\mr {diff} - \mu _0|}{\sigma } \\ \]
Two-Sample Satterthwaite t Test Assuming Unequal Variances (TEST=DIFF_SATT)

The hypotheses for the two-sample Satterthwaite t test are

$\displaystyle H_{0}\colon $
$\displaystyle \mu _\mr {diff}=\mu _0 $
$\displaystyle H_{1}\colon $
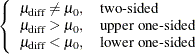$\displaystyle \left\{ \begin{array}{ll} \mu _\mr {diff} \ne \mu _0, & \mbox{two-sided} \\ \mu _\mr {diff} > \mu _0, & \mbox{upper one-sided} \\ \mu _\mr {diff} < \mu _0, & \mbox{lower one-sided} \\ \end{array} \right. $

The test assumes normally distributed data and requires $N \ge 3$, $n_1 \ge 1$, and $n_2 \ge 1$. The test statistics are

$\displaystyle t $
$\displaystyle = \frac{\bar{x}_2-\bar{x}_1-\mu _0}{\left[\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right]^\frac {1}{2}} = N^\frac {1}{2} \frac{\bar{x}_2-\bar{x}_1-\mu _0}{\left[\frac{s_1^2}{w_1} + \frac{s_2^2}{w_2}\right]^\frac {1}{2}} $
$\displaystyle F $
$\displaystyle = t^2 $

where $\bar{x}_1$ and $\bar{x}_2$ are the sample means and $s_1$ and $s_2$ are the sample standard deviations.

DiSantostefano and Muller (1995, p. 585) state, the test is based on assuming that under $H_0$, F is distributed as $F(1,\nu )$, where $\nu $ is given by Satterthwaite’s approximation (Satterthwaite, 1946),

\[ \nu = \frac{\left[\frac{\sigma _1^2}{n_1} + \frac{\sigma _2^2}{n_2}\right]^2}{\frac{\left[\frac{\sigma _1^2}{n_1}\right]^2}{n_1-1} + \frac{\left[\frac{\sigma _2^2}{n_2}\right]^2}{n_2-1}} = \frac{\left[\frac{\sigma _1^2}{w_1} + \frac{\sigma _2^2}{w_2}\right]^2}{\frac{\left[\frac{\sigma _1^2}{w_1}\right]^2}{N w_1-1} + \frac{\left[\frac{\sigma _2^2}{w_2}\right]^2}{N w_2-1}} \]

Since $\nu $ is unknown, in practice it must be replaced by an estimate

\[ \hat{\nu } = \frac{\left[\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right]^2}{\frac{\left[\frac{s_1^2}{n_1}\right]^2}{n_1-1} + \frac{\left[\frac{s_2^2}{n_2}\right]^2}{n_2-1}} = \frac{\left[\frac{s_1^2}{w_1} + \frac{s_2^2}{w_2}\right]^2}{\frac{\left[\frac{s_1^2}{w_1}\right]^2}{N w_1-1} + \frac{\left[\frac{s_2^2}{w_2}\right]^2}{N w_2-1}} \]

So the test is

\[ \mbox{Reject} \quad H_0 \quad \mbox{if} \left\{ \begin{array}{ll} F \ge F_{1-\alpha }(1, \hat{\nu }), & \mbox{two-sided} \\ t \ge t_{1-\alpha }(\hat{\nu }), & \mbox{upper one-sided} \\ t \le t_{\alpha }(\hat{\nu }), & \mbox{lower one-sided} \\ \end{array} \right. \]

Exact solutions for power for the two-sided and upper one-sided cases are given in Moser, Stevens, and Watts (1989). The lower one-sided case follows easily by using symmetry. The equations are as follows:

$\displaystyle \mr {power} $
$\displaystyle = \left\{ \begin{array}{ll} \int _0^\infty P\left(F(1,N-2, \lambda ) > \right. \\ \quad \left. h(u) F_{1-\alpha }(1, v(u)) | u\right) f(u) \mr {d}u, & \mbox{two-sided} \\ \int _0^\infty P\left(t(N-2, \lambda ^\frac {1}{2}) > \right. \\ \quad \left. \left[h(u)\right]^\frac {1}{2} t_{1-\alpha }(v(u)) | u\right) f(u) \mr {d}u, & \mbox{upper one-sided} \\ \int _0^\infty P\left(t(N-2, \lambda ^\frac {1}{2}) < \right. \\ \quad \left. \left[h(u)\right]^\frac {1}{2} t_{\alpha }(v(u)) | u\right) f(u) \mr {d}u, & \mbox{lower one-sided} \\ \end{array} \right. $
$\displaystyle \mbox{where} $
$\displaystyle $
$\displaystyle h(u) $
$\displaystyle = \frac{\left(\frac{1}{n_1} + \frac{u}{n_2}\right) (n_1+n_2-2)}{\left[(n_1-1) + (n_2-1)\frac{u\sigma _1^2}{\sigma _2^2}\right] \left(\frac{1}{n_1} + \frac{\sigma _2^2}{\sigma _1^2n_2}\right)} $
$\displaystyle v(u) $
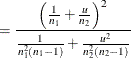$\displaystyle = \frac{\left(\frac{1}{n_1} + \frac{u}{n_2}\right)^2}{\frac{1}{n_1^2(n_1-1)} + \frac{u^2}{n_2^2(n_2-1)}} $
$\displaystyle \lambda $
$\displaystyle = \frac{(\mu _\mr {diff}-\mu _0)^2}{\frac{\sigma _1^2}{n_1} + \frac{\sigma _2^2}{n_2}} $
$\displaystyle f(u) $
$\displaystyle = \frac{\Gamma \left(\frac{n_1+n_2-2}{2}\right)}{\Gamma \left(\frac{n_1-1}{2}\right) \Gamma \left(\frac{n_2-1}{2}\right)} \left[ \frac{\sigma _1^2(n_2-1)}{\sigma _2^2(n_1-1)}\right]^\frac {n_2-1}{2} u^\frac {n_2-3}{2} \left[1+\left(\frac{n_2-1}{n_1-1}\right) \frac{u\sigma _1^2}{\sigma _2^2}\right]^{-\left(\frac{n_1+n_2-2}{2}\right)} $

The density $f(u)$ is obtained from the fact that

\[ \frac{u\sigma _1^2}{\sigma _2^2} \sim F(n_2-1,n_1-1) \]
Two-Sample Pooled t Test of Mean Ratio with Lognormal Data (TEST=RATIO)

The lognormal case is handled by reexpressing the analysis equivalently as a normality-based test on the log-transformed data, by using properties of the lognormal distribution as discussed in Johnson, Kotz, and Balakrishnan (1994, Chapter 14). The approaches in the section Two-Sample t Test Assuming Equal Variances (TEST=DIFF) then apply.

In contrast to the usual t test on normal data, the hypotheses with lognormal data are defined in terms of geometric means rather than arithmetic means. The test assumes equal coefficients of variation in the two groups.

The hypotheses for the two-sample t test with lognormal data are

$\displaystyle H_{0}\colon $
$\displaystyle \frac{\gamma _2}{\gamma _1} = \gamma _0 $
$\displaystyle H_{1}\colon $
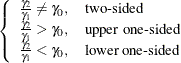$\displaystyle \left\{ \begin{array}{ll} \frac{\gamma _2}{\gamma _1} \ne \gamma _0, & \mbox{two-sided} \\ \frac{\gamma _2}{\gamma _1} > \gamma _0, & \mbox{upper one-sided} \\ \frac{\gamma _2}{\gamma _1} < \gamma _0, & \mbox{lower one-sided} \\ \end{array} \right. $

Let $\mu _1^\star $, $\mu _2^\star $, and $\sigma ^\star $ be the (arithmetic) means and common standard deviation of the corresponding normal distributions of the log-transformed data. The hypotheses can be rewritten as follows:

$\displaystyle H_{0}\colon $
$\displaystyle \mu _2^\star - \mu _1^\star = \log (\gamma _0) $
$\displaystyle H_{1}\colon $
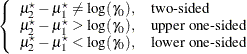$\displaystyle \left\{ \begin{array}{ll} \mu _2^\star - \mu _1^\star \ne \log (\gamma _0), & \mbox{two-sided} \\ \mu _2^\star - \mu _1^\star > \log (\gamma _0), & \mbox{upper one-sided} \\ \mu _2^\star - \mu _1^\star < \log (\gamma _0), & \mbox{lower one-sided} \\ \end{array} \right. $

where

$\displaystyle \mu _1^\star $
$\displaystyle = \log \gamma _1 $
$\displaystyle \mu _2^\star $
$\displaystyle = \log \gamma _2 $

The test assumes lognormally distributed data and requires $N \ge 3$, $n_1 \ge 1$, and $n_2 \ge 1$.

The power is

\[ \mr {power} = \left\{ \begin{array}{ll} P\left(F(1, N-2, \delta ^2) \ge F_{1-\alpha }(1, N-2)\right), & \mbox{two-sided} \\ P\left(t(N-2, \delta ) \ge t_{1-\alpha }(N-2)\right), & \mbox{upper one-sided} \\ P\left(t(N-2, \delta ) \le t_{\alpha }(N-2)\right), & \mbox{lower one-sided} \\ \end{array} \right. \]

where

$\displaystyle \delta $
$\displaystyle = N^\frac {1}{2} (w_1 w_2)^\frac {1}{2} \left( \frac{\mu _2^\star - \mu _1^\star - \log (\gamma _0)}{\sigma ^\star } \right) $
$\displaystyle \sigma ^\star $
$\displaystyle = \left[ \log (\mr {CV}^2 + 1) \right]^\frac {1}{2} $
Additive Equivalence Test for Mean Difference with Normal Data (TEST=EQUIV_DIFF)

The hypotheses for the equivalence test are

$\displaystyle H_{0}\colon $
$\displaystyle \mu _\mr {diff} < \theta _ L \quad \mbox{or}\quad \mu _\mr {diff} > \theta _ U $
$\displaystyle H_{1}\colon $
$\displaystyle \theta _ L \le \mu _\mr {diff} \le \theta _ U $

The analysis is the two one-sided tests (TOST) procedure of Schuirmann (1987). The test assumes normally distributed data and requires $N \ge 3$, $n_1 \ge 1$, and $n_2 \ge 1$. Phillips (1990) derives an expression for the exact power assuming a balanced design; the results are easily adapted to an unbalanced design:

$\displaystyle \mr {power} $
$\displaystyle = Q_{N-2}\left((-t_{1-\alpha }(N-2)),\frac{\mu _\mr {diff}-\theta _ U}{\sigma N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}}}; 0,\frac{(N-2)^\frac {1}{2}(\theta _ U-\theta _ L)}{2\sigma N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}}(t_{1-\alpha }(N-2))}\right) \quad - $
$\displaystyle $
$\displaystyle \quad Q_{N-2}\left((t_{1-\alpha }(N-2)),\frac{\mu _\mr {diff}-\theta _ L}{\sigma N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}}}; 0,\frac{(N-2)^\frac {1}{2}(\theta _ U-\theta _ L)}{2\sigma N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}} (t_{1-\alpha }(N-2))}\right) $

where $Q_\cdot (\cdot ,\cdot ;\cdot ,\cdot )$ is Owen’s Q function, defined in the section Common Notation.

Multiplicative Equivalence Test for Mean Ratio with Lognormal Data (TEST=EQUIV_RATIO)

The lognormal case is handled by reexpressing the analysis equivalently as a normality-based test on the log-transformed data, by using properties of the lognormal distribution as discussed in Johnson, Kotz, and Balakrishnan (1994, Chapter 14). The approaches in the section Additive Equivalence Test for Mean Difference with Normal Data (TEST=EQUIV_DIFF) then apply.

In contrast to the additive equivalence test on normal data, the hypotheses with lognormal data are defined in terms of geometric means rather than arithmetic means.

The hypotheses for the equivalence test are

$\displaystyle H_{0}\colon $
$\displaystyle \frac{\gamma _ T}{\gamma _ R} \le \theta _ L \quad \mbox{or}\quad \frac{\gamma _ T}{\gamma _ R} \ge \theta _ U $
$\displaystyle H_{1}\colon $
$\displaystyle \theta _ L < \frac{\gamma _ T}{\gamma _ R} < \theta _ U $
\[ \mbox{where}\quad 0 < \theta _ L < \theta _ U \]

The analysis is the two one-sided tests (TOST) procedure of Schuirmann (1987) on the log-transformed data. The test assumes lognormally distributed data and requires $N \ge 3$, $n_1 \ge 1$, and $n_2 \ge 1$. Diletti, Hauschke, and Steinijans (1991) derive an expression for the exact power assuming a crossover design; the results are easily adapted to an unbalanced two-sample design:

$\displaystyle \mr {power} $
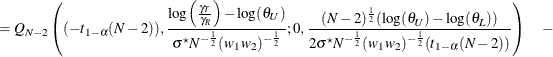$\displaystyle = Q_{N-2}\left((-t_{1-\alpha }(N-2)),\frac{\log \left(\frac{\gamma _ T}{\gamma _ R}\right)- \log (\theta _ U)}{\sigma ^\star N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}}}; 0,\frac{(N-2)^\frac {1}{2} (\log (\theta _ U)-\log (\theta _ L))}{2\sigma ^\star N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}} (t_{1-\alpha }(N-2))}\right) \quad - $
$\displaystyle $
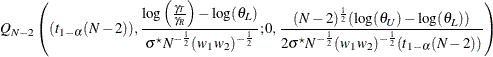$\displaystyle \quad Q_{N-2}\left((t_{1-\alpha }(N-2)),\frac{\log \left(\frac{\gamma _ T}{\gamma _ R}\right)- \log (\theta _ L)}{\sigma ^\star N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}}}; 0,\frac{(N-2)^\frac {1}{2} (\log (\theta _ U)-\log (\theta _ L))}{2\sigma ^\star N^{-\frac{1}{2}}(w_1 w_2)^{-\frac{1}{2}}(t_{1-\alpha }(N-2))}\right) $

where

\[ \sigma ^\star = \left[ \log (\mr {CV}^2+1) \right]^\frac {1}{2} \]

is the (assumed common) standard deviation of the normal distribution of the log-transformed data, and $Q_\cdot (\cdot ,\cdot ;\cdot ,\cdot )$ is Owen’s Q function, defined in the section Common Notation.

Confidence Interval for Mean Difference (CI=DIFF)

This analysis of precision applies to the standard t-based confidence interval:

\[ \begin{array}{ll} \left[ (\bar{x}_2 - \bar{x}_1) - t_{1-\frac{\alpha }{2}}(N-2) \frac{s_ p}{\sqrt {N w_1 w_2}}, \right. \\ \quad \left. (\bar{x}_2 - \bar{x}_1) + t_{1-\frac{\alpha }{2}}(N-2) \frac{s_ p}{\sqrt {N w_1 w_2}} \right], & \mbox{two-sided} \\ \left[ (\bar{x}_2 - \bar{x}_1) - t_{1-\alpha }(N-2) \frac{s_ p}{\sqrt {N w_1 w_2}}, \quad \infty \right), & \mbox{upper one-sided} \\ \left( -\infty , \quad (\bar{x}_2 - \bar{x}_1) + t_{1-\alpha }(N-2) \frac{s_ p}{\sqrt {N w_1 w_2}} \right], & \mbox{lower one-sided} \\ \end{array} \]

where $\bar{x}_1$ and $\bar{x}_2$ are the sample means and $s_ p$ is the pooled standard deviation. The “half-width” is defined as the distance from the point estimate $\bar{x}_2 - \bar{x}_1$ to a finite endpoint,

\[ \mbox{half-width} = \left\{ \begin{array}{ll} t_{1-\frac{\alpha }{2}}(N-2) \frac{s_ p}{\sqrt {N w_1 w_2}}, & \mbox{two-sided} \\ t_{1-\alpha }(N-2) \frac{s_ p}{\sqrt {N w_1 w_2}}, & \mbox{one-sided} \\ \end{array} \right. \]

A “valid” conference interval captures the true mean. The exact probability of obtaining at most the target confidence interval half-width h, unconditional or conditional on validity, is given by Beal (1989):

$\displaystyle \mbox{Pr(half-width $\le h$)} $
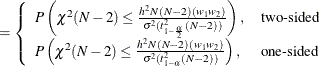$\displaystyle = \left\{ \begin{array}{ll} P\left( \chi ^2(N-2) \le \frac{h^2 N(N-2)(w_1w_2)}{\sigma ^2(t^2_{1-\frac{\alpha }{2}}(N-2))} \right), & \mbox{two-sided} \\ P\left( \chi ^2(N-2) \le \frac{h^2 N(N-2)(w_1w_2)}{\sigma ^2(t^2_{1-\alpha }(N-2))} \right), & \mbox{one-sided} \\ \end{array} \right. $
$\displaystyle \begin{array}{r} \mbox{Pr(half-width $\le h$ |} \\ \mbox{validity)} \end{array} $
$\displaystyle = \left\{ \begin{array}{ll} \left(\frac{1}{1-\alpha }\right) 2 \left[ Q_{N-2}\left((t_{1-\frac{\alpha }{2}}(N-2)),0; \right. \right. \\ \quad \left. \left. 0,b_2\right) - Q_{N-2}(0,0;0,b_2)\right], & \mbox{two-sided} \\ \left(\frac{1}{1-\alpha }\right) Q_{N-2}\left((t_{1-\alpha }(N-2)),0;0,b_2\right), & \mbox{one-sided} \\ \end{array} \right. $

where

$\displaystyle b_2 $
$\displaystyle = \frac{h(N-2)^\frac {1}{2}}{\sigma (t_{1-\frac{\alpha }{c}}(N-2)) N^{-\frac{1}{2}}(w_1w_2)^{-\frac{1}{2}}} $
$\displaystyle c $
$\displaystyle = \mbox{number of sides} $

and $Q_\cdot (\cdot ,\cdot ;\cdot ,\cdot )$ is Owen’s Q function, defined in the section Common Notation.

A “quality” confidence interval is both sufficiently narrow (half-width $\le h$) and valid:

$\displaystyle \mbox{Pr(quality)} $
$\displaystyle = \mbox{Pr(half-width $\le h$ and validity)} $
$\displaystyle $
$\displaystyle = \mbox{Pr(half-width $\le h$ | validity)($1-\alpha $)} $
Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.