The MIXED Procedure

You can reference every graph produced through ODS Graphics with a name. The names of the graphs that PROC MIXED generates are listed in Table 59.28, along with the required statements and options.

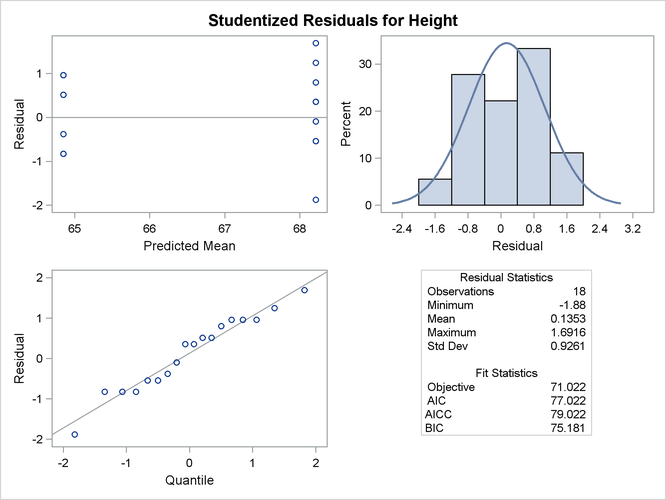
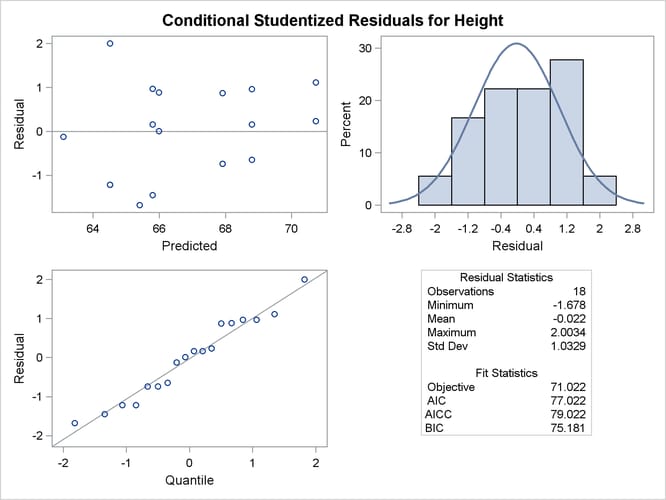
The MIXED procedure can generate panels of residual diagnostics. Each panel consists of a plot of residuals versus predicted values, a histogram with normal density overlaid, a Q-Q plot, and summary residual and fit statistics (Figure 59.15). The plots are produced even if the OUTP= and OUTPM= options in the MODEL statement are not specified. Residual panels can be generated for marginal and conditional raw, studentized, and Pearson residuals as well as for scaled residuals (see the section Residual Diagnostics).

Recall the example in the section Getting Started: MIXED Procedure. The following statements generate several panels of residual graphs:

ods graphics on;
proc mixed data=heights plots=studentpanel(marginal conditional);
   class Family Gender;
   model Height = Gender / residual;
   random Family Family*Gender;
run;
ods graphics off;

The graphs are created when ODS Graphics is enabled. The panel of the studentized marginal residuals is shown in Figure 59.15, and the panel of the studentized conditional residuals is shown in Figure 59.16.

Since the fixed-effects part of the model comprises only an intercept and the gender effect, the marginal mean takes on only two values, one for each gender. The “Residual Statistics” inset in the lower-right corner provides descriptive statistics for the set of residuals that is displayed. Note that residuals in a mixed model do not necessarily sum to zero, even if the model contains an intercept.

The graphical features of the MIXED procedure enable you to generate plots of influence diagnostics and of deletion estimates. The type and number of plots produced depend on your modifiers of the INFLUENCE option in the MODEL statement and on the PLOTS= option in the PROC MIXED statement. Plots related to covariance parameters are produced only when diagnostics are computed by iterative methods (ITER=). The estimates of the fixed effects—and covariance parameters when updates are iterative—are plotted when you specify the ESTIMATES modifier or when you request PLOTS=INFLUENCEESTPLOT.

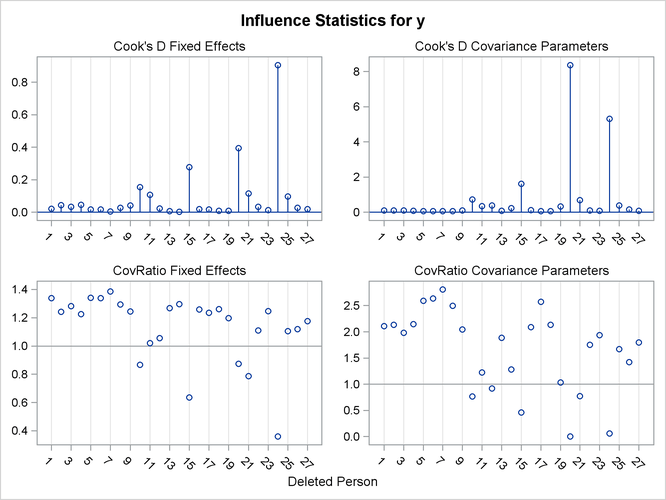
Two basic types of influence panels are shown in Figure 59.17 and Figure 59.18. The diagnostics panel shows Cook’s D and CovRatio statistics for the fixed effects and the covariance parameters. For the SAS statements that produce these influence panels, see Example 59.8. In this example, the impact of subjects (Person) on the analysis is assessed. The Cook’s D statistic measures a subject’s impact on the estimates, and the CovRatio statistic measures a subject’s impact on the precision of the estimates. Separate statistics are computed for the fixed effects and the covariance parameters. The CovRatio statistic has a threshold of 1.0. Values larger than 1.0 indicate that precision of the estimates is lost by exclusion of the observations in question. Values smaller than 1.0 indicate that precision is gained by exclusion of the observations from the analysis. For example, it is evident from Figure 59.17 that person 20 has considerable impact on the covariance parameter estimates and moderate influence on the fixed-effects estimates. Furthermore, exclusion of this subject from the analysis increases the precision of the covariance parameters, whereas the effect on the precision of the fixed effects is minor.

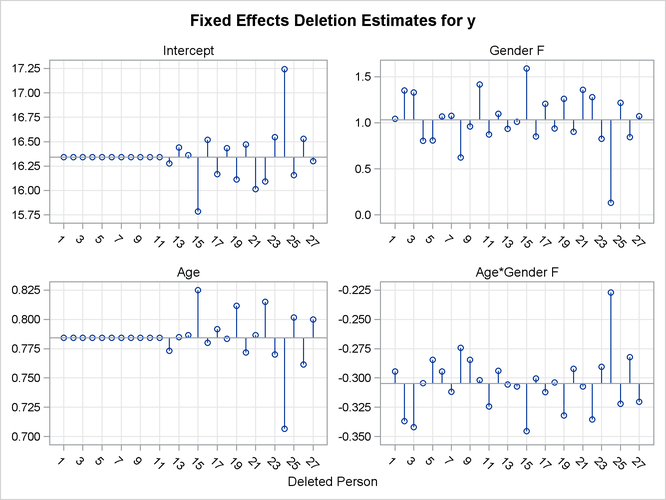
Figure 59.18 shows another type of influence plot, a panel of the deletion estimates. Each plot within the panel corresponds to one of the model parameters. A reference line is drawn at the estimate based on the full data.