The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputODS Table NamesODS Graphics
Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Example 79.1 Modeling Salaries of Major League Baseball Players
This example features the use of ODS Graphics in the process of building models by using the REG procedure and highlights the use of fit and influence diagnostics.
The following data set contains salary and performance information for Major League Baseball players who played at least one game in both the 1986 and 1987 seasons, excluding pitchers. The salaries (Sports Illustrated, April 20, 1987) are for the 1987 season and the performance measures are from 1986 (Collier Books, The 1987 Baseball Encyclopedia Update).
data baseball;
length name $ 18;
length team $ 12;
input name $ 1-18 no_atbat no_hits no_home no_runs no_rbi no_bb yr_major
cr_atbat cr_hits cr_home cr_runs cr_rbi cr_bb league $
division $ team $ position $ no_outs no_assts no_error salary;
logSalary = log10(salary);
label name="Player's Name"
no_hits="Hits in 1986"
no_runs="Runs in 1986"
no_rbi="RBIs in 1986"
no_bb="Walks in 1986"
yr_major="Years in MLB"
cr_hits="Career Hits"
salary="1987 Salary in $ Thousands"
logSalary = "log10(Salary)";
datalines;
Allanson, Andy 293 66 1 30 29 14
1 293 66 1 30 29 14
American East Cleveland C 446 33 20 .
Ashby, Alan 315 81 7 24 38 39
14 3449 835 69 321 414 375
National West Houston C 632 43 10 475
Davis, Alan 479 130 18 66 72 76
3 1624 457 63 224 266 263
American West Seattle 1B 880 82 14 480
Dawson, Andre 496 141 20 65 78 37
11 5628 1575 225 828 838 354
National East Montreal RF 200 11 3 500
Galarraga, Andres 321 87 10 39 42 30
2 396 101 12 48 46 33
National East Montreal 1B 805 40 4 91.5
Griffin, Alfredo 594 169 4 74 51 35
11 4408 1133 19 501 336 194
American West Oakland SS 282 421 25 750
... more lines ...
Wilson, Willie 631 170 9 77 44 31
11 4908 1457 30 775 357 249
American West KansasCity CF 408 4 3 1000
;
Suppose you want to investigate whether you can model the players’ salaries for the 1987 season based on batting statistics for the previous season and lifetime batting performance. Since the variation in salaries is much greater for higher salaries, it is appropriate to apply a log transformation for this analysis. The following statements begin the analysis:
ods graphics on; proc reg data=baseball; id name team league; model logSalary = no_hits no_runs no_rbi no_bb yr_major cr_hits; run;
Output 79.1.1 shows the default output produced by PROC REG. The number of observations table shows that 59 observations are excluded because they have missing values for at least one of the variables used in the analysis. The analysis of variance and parameter estimates tables provide details about the fitted model.
Output 79.1.1: Default Output from PROC REG
| Number of Observations Read | 322 |
|---|---|
| Number of Observations Used | 263 |
| Number of Observations with Missing Values | 59 |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 6 | 22.92208 | 3.82035 | 60.56 | <.0001 |
| Error | 256 | 16.14954 | 0.06308 | ||
| Corrected Total | 262 | 39.07162 | |||
| Root MSE | 0.25117 | R-Square | 0.5867 |
|---|---|---|---|
| Dependent Mean | 2.57416 | Adj R-Sq | 0.5770 |
| Coeff Var | 9.75719 |
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | Label | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | Intercept | 1 | 1.80065 | 0.05912 | 30.46 | <.0001 |
| no_hits | Hits in 1986 | 1 | 0.00288 | 0.00091244 | 3.15 | 0.0018 |
| no_runs | Runs in 1986 | 1 | 0.00008638 | 0.00173 | 0.05 | 0.9602 |
| no_rbi | RBIs in 1986 | 1 | 0.00054382 | 0.00102 | 0.53 | 0.5947 |
| no_bb | Walks in 1986 | 1 | 0.00292 | 0.00104 | 2.81 | 0.0054 |
| yr_major | Years in MLB | 1 | 0.03087 | 0.00836 | 3.69 | 0.0003 |
| cr_hits | Career Hits | 1 | 0.00010384 | 0.00006328 | 1.64 | 0.1020 |
Before you accept a regression model, it is important to examine influence and fit diagnostics to see whether the model might be unduly influenced by a few observations and whether the data support the assumptions that underlie the linear regression. To facilitate such investigations, you can obtain diagnostic plots by enabling ODS Graphics.
Output 79.1.2: Fit Diagnostics
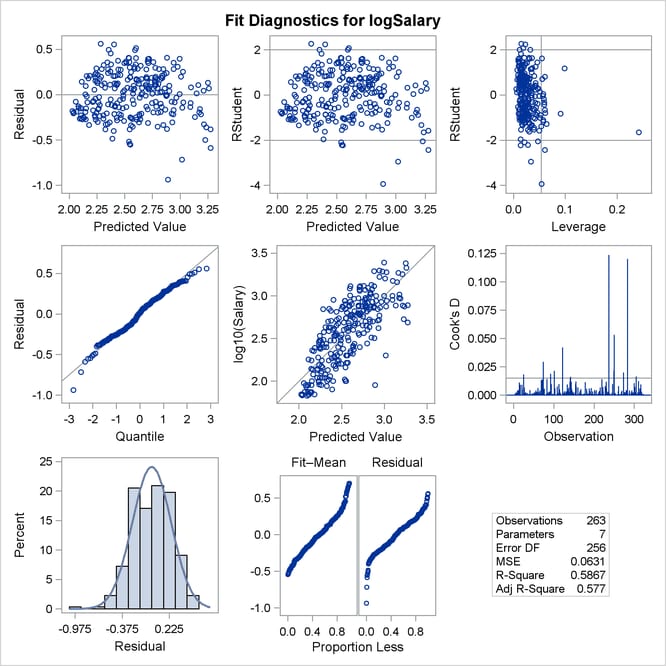
Output 79.1.2 shows a panel of diagnostic plots. The plot of externally studentized residuals (RStudent) by leverage values reveals that there is one observation with very high leverage that might be overly influencing the fit produced. The plot of Cook’s D by observation also indicates two highly influential observations. To investigate further, you can use the PLOTS= option in the PROC REG statement as follows to produce labeled versions of these plots:
proc reg data=baseball
plots(only label)=(RStudentByLeverage CooksD);
id name team league;
model logSalary = no_hits no_runs no_rbi no_bb yr_major cr_hits;
run;
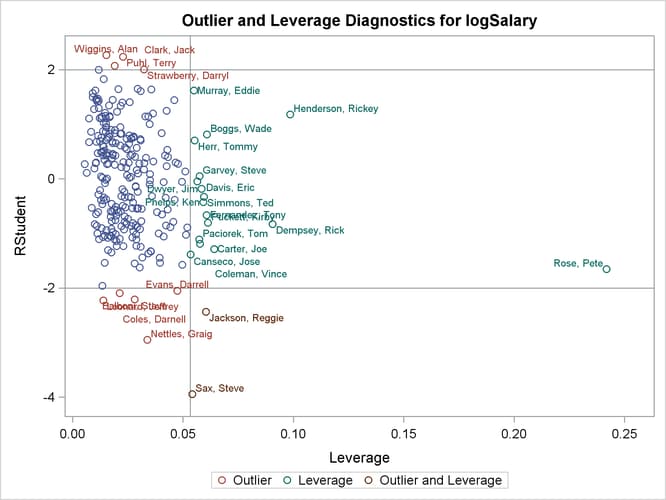
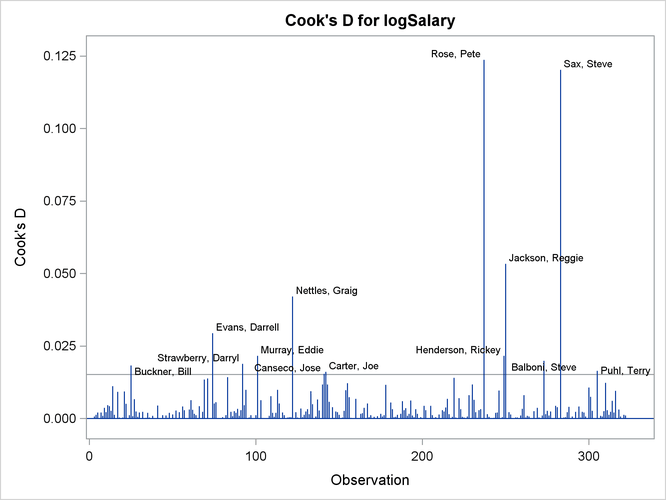
Output 79.1.3 and Output 79.1.4 reveal that Pete Rose is the highly influential observation. You might obtain a better fit to the remaining data if you omit his statistics when building the model.
Output 79.1.3: Outlier and Leverage Diagnostics
Output 79.1.4: Cook’s D
The following statements use a WHERE statement to omit Pete Rose’s statistics when building the model. An alternative way to do this within PROC REG is to use a REWEIGHT statement. See Reweighting Observations in an Analysis for details about reweighting.
proc reg data=baseball
plots=(RStudentByLeverage(label) residuals(smooth));
where name^="Rose, Pete";
id name team league;
model logSalary = no_hits no_runs no_rbi no_bb yr_major cr_hits;
run;
Output 79.1.5 shows the new fit diagnostics panel. You can see that there are still several influential and outlying observations. One possible reason for observing outliers is that the linear model specified is not appropriate to capture the variation in this data. You can often see evidence of an inappropriate model by observing patterns in plots of residuals.
Output 79.1.5: Fit Diagnostics
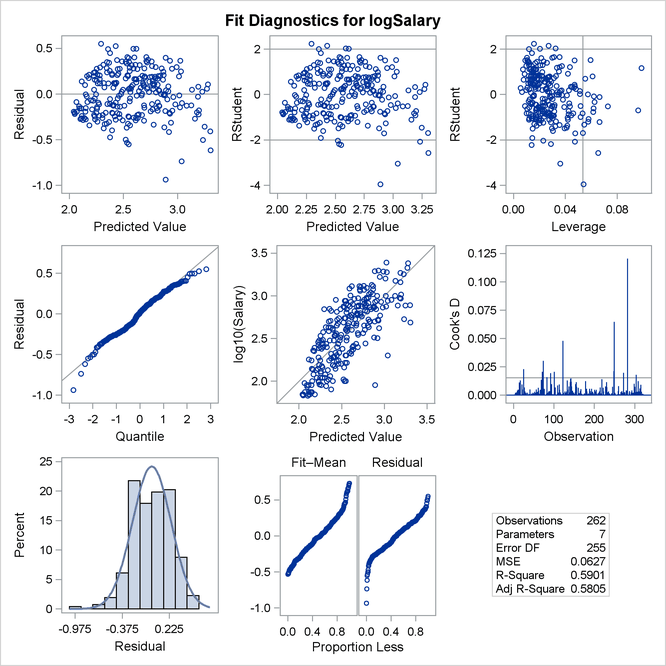
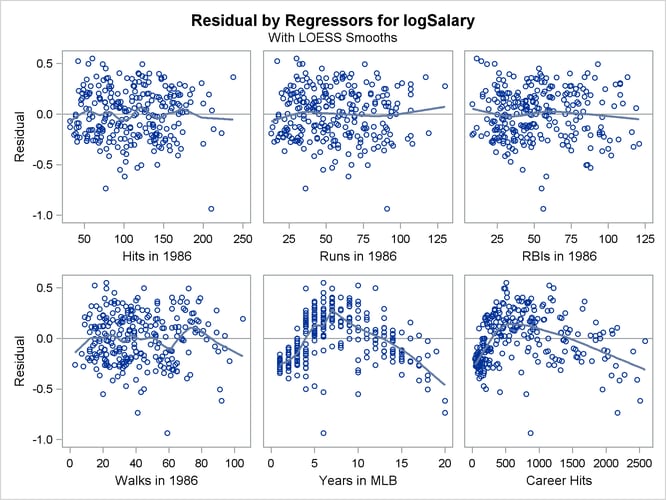
Output 79.1.6 shows plots of the residuals by the regressors in the model. When you specify the RESIDUALS(SMOOTH) suboption of the PLOTS
option in the PROC REG statement, a loess fit is overlaid on each of these plots. You can see the same clear pattern in the residual plots for yr_major and cr_hits. Players near the start of their careers and players near the end of their careers get paid less than the model predicts.
Output 79.1.6: Residuals by Regressors
You can address this lack of fit by using polynomials of degree 2 for these two variables as shown in the following statements:
data baseball;
set baseball(where=(name^="Rose, Pete"));
yr_major2 = yr_major*yr_major;
cr_hits2 = cr_hits*cr_hits;
run;
proc reg data=baseball
plots=(diagnostics(stats=none) RStudentByLeverage(label)
CooksD(label) Residuals(smooth)
DFFITS(label) DFBETAS ObservedByPredicted(label));
id name team league;
model logSalary = no_hits no_runs no_rbi no_bb yr_major cr_hits
yr_major2 cr_hits2;
run;
ods graphics off;
Output 79.1.7 shows the analysis of variance and parameter estimates for this model. Note that the R-square value of 0.787 for this model is considerably larger than the R-square value of 0.587 for the initial model shown in Output 79.1.1.
Output 79.1.7: Output from PROC REG
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 8 | 30.69367 | 3.83671 | 117.13 | <.0001 |
| Error | 253 | 8.28706 | 0.03276 | ||
| Corrected Total | 261 | 38.98073 | |||
| Root MSE | 0.18098 | R-Square | 0.7874 |
|---|---|---|---|
| Dependent Mean | 2.57301 | Adj R-Sq | 0.7807 |
| Coeff Var | 7.03393 |
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | Label | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | Intercept | 1 | 1.64564 | 0.05030 | 32.72 | <.0001 |
| no_hits | Hits in 1986 | 1 | -0.00005539 | 0.00069200 | -0.08 | 0.9363 |
| no_runs | Runs in 1986 | 1 | 0.00093586 | 0.00125 | 0.75 | 0.4549 |
| no_rbi | RBIs in 1986 | 1 | 0.00187 | 0.00074649 | 2.51 | 0.0127 |
| no_bb | Walks in 1986 | 1 | 0.00218 | 0.00075057 | 2.90 | 0.0040 |
| yr_major | Years in MLB | 1 | 0.10383 | 0.01495 | 6.94 | <.0001 |
| cr_hits | Career Hits | 1 | 0.00073955 | 0.00011970 | 6.18 | <.0001 |
| yr_major2 | 1 | -0.00625 | 0.00071687 | -8.73 | <.0001 | |
| cr_hits2 | 1 | -1.44072E-7 | 4.348471E-8 | -3.31 | 0.0011 | |
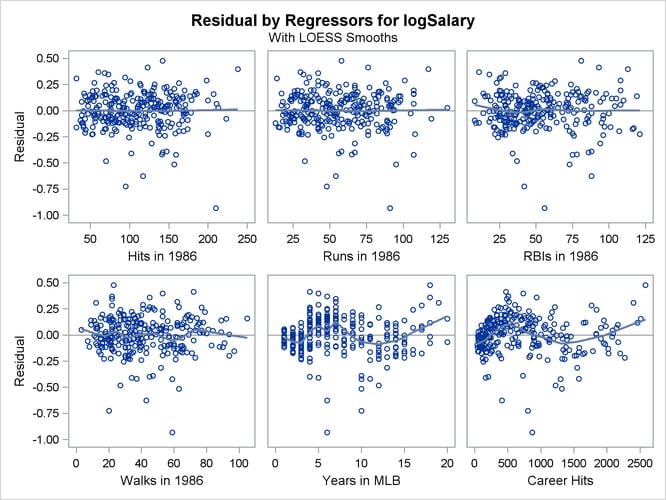
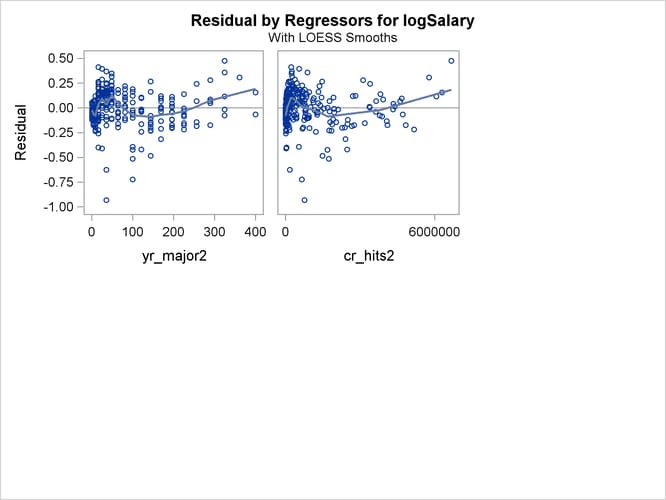
The plots of residuals by regressors in Output 79.1.8 and Output 79.1.9 show that the strong pattern in the plots for cr_majors and cr_hits has been reduced, although there is still some indication of a pattern remaining in these residuals. This suggests that a
quadratic function might be insufficient to capture dependence of salary on these regressors.
Output 79.1.8: Residuals by Regressors
Output 79.1.9: Residuals by Regressors
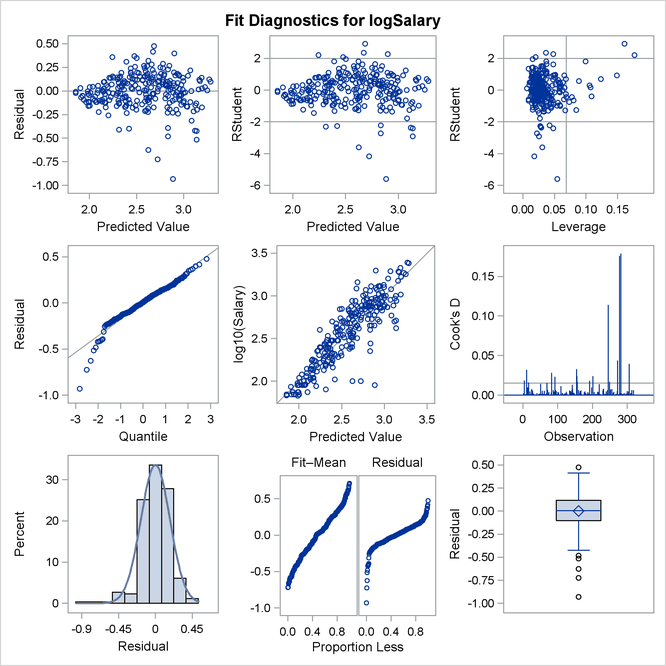
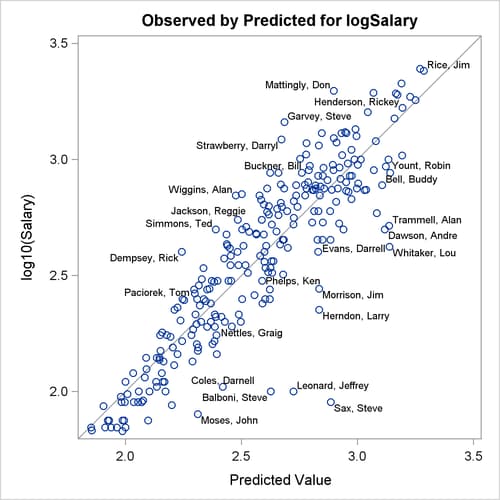
Output 79.1.10 show the diagnostics plots; three of the plots, with points of interest labeled, are shown individually in Output 79.1.11, Output 79.1.12, and Output 79.1.13. The STATS=NONE suboption specified in the PLOTS=DIAGNOSTICS option replaces the inset of statistics with a box plot of the residuals in the fit diagnostics panel. The observed by predicted value plot reveals a reasonably successful model for explaining the variation in salary for most of the players. However, the model tends to overpredict the salaries of several players near the lower end of the salary range. This bias can also be seen in the distribution of the residuals that you can see in the histogram, Q-Q plot, and box plot in Output 79.1.10.
Output 79.1.10: Fit Diagnostics
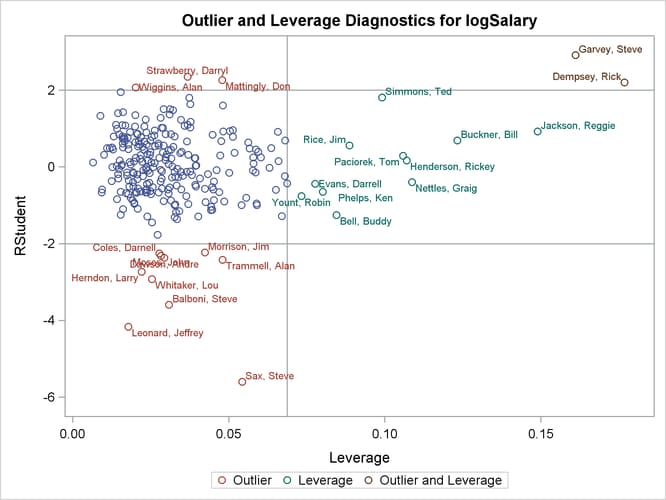
Output 79.1.11: Outlier and Leverage Diagnostics
Output 79.1.12: Observed by Predicted Values
Output 79.1.13: Cook’s D
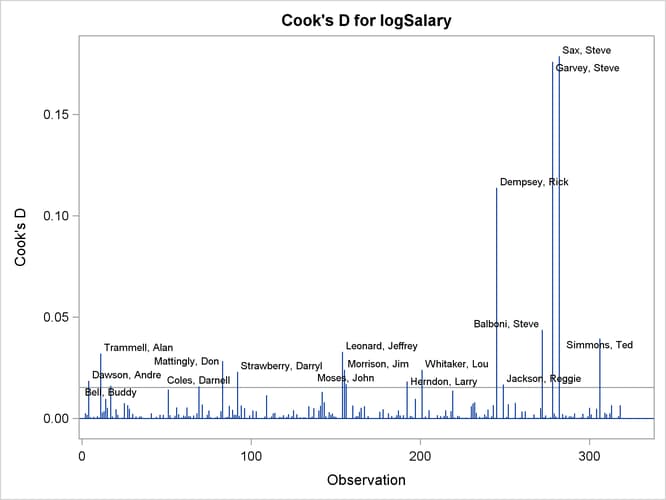
The RStudent by leverage plot in Output 79.1.11 and the Cook’s D plot in Output 79.1.13 show that there are still a number of influential observations. By specifying the DFFITS and DFBETAS suboptions of the PLOTS= option, you obtain additional influence diagnostics plots shown in Output 79.1.14 and Output 79.1.15. See Influence Statistics for details about the interpretation DFFITS and DFBETAS statistics.
Output 79.1.14: DFFITS
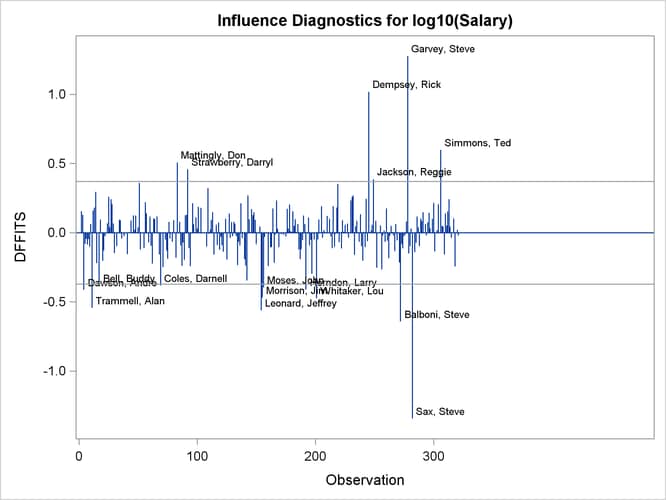
Output 79.1.15: DFBETAS
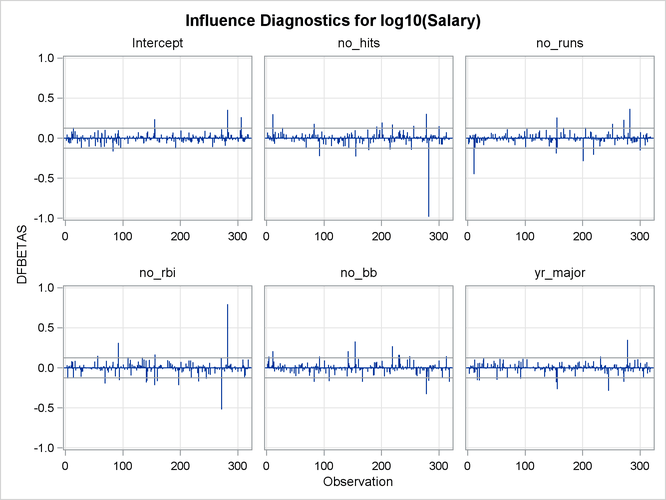
You can continue this analysis by investigating how the influential observations identified in the various influence plots affect the fit. You can also use PROC ROBUSTREG to obtain a fit that is resistant to the presence of high leverage points and outliers.