The KRIGE2D Procedure
The Nugget Effect
For all the semivariogram models considered previously, the following property holds:
|
|
However, a plot of the experimental semivariogram might indicate a discontinuity at h = 0; that is, ![]() as
as ![]() , while
, while ![]() . The quantity
. The quantity ![]() is called the nugget effect; this term is from mining geostatistics where nuggets literally exist, and it represents variations at a much smaller scale
than any of the measured pairwise distances—that is, at distances
is called the nugget effect; this term is from mining geostatistics where nuggets literally exist, and it represents variations at a much smaller scale
than any of the measured pairwise distances—that is, at distances ![]() , where
, where
|
|
Nonzero nugget effects have been associated with conceptual and theoretical difficulties; see Cressie (1993, section 2.3.1) and Christakos (1992, section 7.4.3) for details. There is no practical difficulty, however; you simply visually extrapolate the experimental semivariogram as ![]() . The importance of availability of data at small lag distances is again illustrated.
. The importance of availability of data at small lag distances is again illustrated.
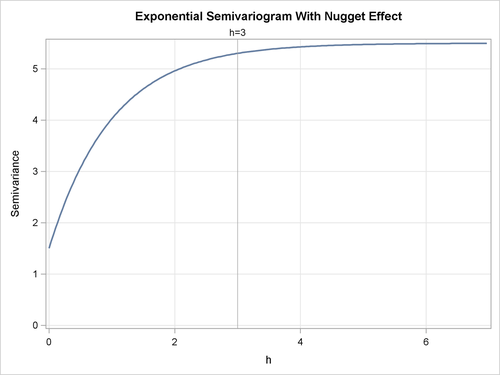
As an example, an exponential semivariogram with a nugget effect ![]() has the form
has the form
|
|
and
|
|
where the factor ![]() is called the partial sill and the sill
is called the partial sill and the sill ![]() .
.
This is illustrated in Figure 49.11 for the parameters ![]() ,
, ![]() , and nugget effect
, and nugget effect ![]() .
.
You can specify the nugget effect in PROC KRIGE2D with the NUGGET= option in the MODEL statement. It is a separate, additive term independent of direction; that is, it is isotropic. The way to approximate an anisotropic nugget effect is described in the following section.
Figure 49.11: Exponential Semivariogram Model with a Nugget Effect ![]()