The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC Statement BY Statement CLASS Statement CLUSTER Statement CONTRAST Statement DOMAIN Statement EFFECT Statement ESTIMATE Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement REPWEIGHTS Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement
PROC SURVEYLOGISTIC Statement BY Statement CLASS Statement CLUSTER Statement CONTRAST Statement DOMAIN Statement EFFECT Statement ESTIMATE Statement FREQ Statement LSMEANS Statement LSMESTIMATE Statement MODEL Statement OUTPUT Statement REPWEIGHTS Statement SLICE Statement STORE Statement STRATA Statement TEST Statement UNITS Statement WEIGHT Statement -
Details
 Missing Values Model Specification Model Fitting Survey Design Information Logistic Regression Models and Parameters Variance Estimation Domain Analysis Hypothesis Testing and Estimation Linear Predictor, Predicted Probability, and Confidence Limits Output Data Sets Displayed Output ODS Table Names ODS Graphics
Missing Values Model Specification Model Fitting Survey Design Information Logistic Regression Models and Parameters Variance Estimation Domain Analysis Hypothesis Testing and Estimation Linear Predictor, Predicted Probability, and Confidence Limits Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples

- References
Score Statistics and Tests
To understand the general form of the score statistics, let 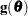 be the vector of first partial derivatives of the log likelihood with respect to the parameter vector
be the vector of first partial derivatives of the log likelihood with respect to the parameter vector 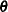 , and let
, and let 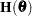 be the matrix of second partial derivatives of the log likelihood with respect to
be the matrix of second partial derivatives of the log likelihood with respect to 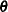 . That is,
. That is, 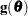 is the gradient vector, and
is the gradient vector, and 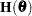 is the Hessian matrix. Let
is the Hessian matrix. Let 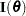 be either
be either 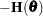 or the expected value of
or the expected value of 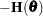 . Consider a null hypothesis
. Consider a null hypothesis 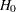 . Let
. Let  be the MLE of
be the MLE of 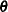 under
under 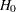 . The chi-square score statistic for testing
. The chi-square score statistic for testing 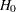 is defined by
is defined by
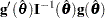 |
It has an asymptotic 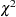 distribution with
distribution with  degrees of freedom under
degrees of freedom under 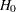 , where
, where  is the number of restrictions imposed on
is the number of restrictions imposed on 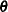 by
by 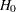 .
.