The RSREG Procedure
Example 78.1 A Saddle Surface Response Using Ridge Analysis
Myers (1976) analyzes an experiment reported by Frankel (1961) aimed at maximizing the yield of mercaptobenzothiazole (MBT) by varying processing time and temperature. Myers (1976) uses a two-factor model in which the estimated surface does not have a unique optimum. A ridge analysis is used to determine the region in which the optimum lies. The objective is to find the settings of time and temperature in the processing of a chemical that maximize the yield. The following statements produce Output 78.1.1 through Output 78.1.6:
data d;
input Time Temp MBT;
label Time = "Reaction Time (Hours)"
Temp = "Temperature (Degrees Centigrade)"
MBT = "Percent Yield Mercaptobenzothiazole";
datalines;
4.0 250 83.8
20.0 250 81.7
12.0 250 82.4
12.0 250 82.9
12.0 220 84.7
12.0 280 57.9
12.0 250 81.2
6.3 229 81.3
6.3 271 83.1
17.7 229 85.3
17.7 271 72.7
4.0 250 82.0
;
ods graphics on; proc rsreg data=d plots=(ridge surface); model MBT=Time Temp / lackfit; ridge max; run; ods graphics off;
Output 78.1.1 displays the coding coefficients for the transformation of the independent variables to lie between 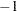 and 1 and some simple statistics for the response variable.
and 1 and some simple statistics for the response variable.
| Coding Coefficients for the Independent Variables |
||
|---|---|---|
| Factor | Subtracted off | Divided by |
| Time | 12.000000 | 8.000000 |
| Temp | 250.000000 | 30.000000 |
| Response Surface for Variable MBT: Percent Yield Mercaptobenzothiazole |
|
|---|---|
| Response Mean | 79.916667 |
| Root MSE | 4.615964 |
| R-Square | 0.8003 |
| Coefficient of Variation | 5.7760 |
Output 78.1.2 shows that the lack of fit for the model is highly significant. Since the quadratic model does not fit the data very well, firm statements about the underlying process should not be based only on the current analysis. Note from the analysis of variance for the model that the test for the time factor is not significant. If further experimentation is undertaken, it might be best to fix Time at a moderate to high value and to concentrate on the effect of temperature. In the actual experiment discussed here, extra runs were made that confirmed the results of the following analysis.
| Regression | DF | Type I Sum of Squares | R-Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Linear | 2 | 313.585803 | 0.4899 | 7.36 | 0.0243 |
| Quadratic | 2 | 146.768144 | 0.2293 | 3.44 | 0.1009 |
| Crossproduct | 1 | 51.840000 | 0.0810 | 2.43 | 0.1698 |
| Total Model | 5 | 512.193947 | 0.8003 | 4.81 | 0.0410 |
| Residual | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Lack of Fit | 3 | 124.696053 | 41.565351 | 39.63 | 0.0065 |
| Pure Error | 3 | 3.146667 | 1.048889 | ||
| Total Error | 6 | 127.842720 | 21.307120 |
| Parameter | DF | Estimate | Standard Error | t Value | Pr > |t| | Parameter Estimate from Coded Data |
|---|---|---|---|---|---|---|
| Intercept | 1 | -545.867976 | 277.145373 | -1.97 | 0.0964 | 82.173110 |
| Time | 1 | 6.872863 | 5.004928 | 1.37 | 0.2188 | -1.014287 |
| Temp | 1 | 4.989743 | 2.165839 | 2.30 | 0.0608 | -8.676768 |
| Time*Time | 1 | 0.021631 | 0.056784 | 0.38 | 0.7164 | 1.384394 |
| Temp*Time | 1 | -0.030075 | 0.019281 | -1.56 | 0.1698 | -7.218045 |
| Temp*Temp | 1 | -0.009836 | 0.004304 | -2.29 | 0.0623 | -8.852519 |
| Factor | DF | Sum of Squares | Mean Square | F Value | Pr > F | Label |
|---|---|---|---|---|---|---|
| Time | 3 | 61.290957 | 20.430319 | 0.96 | 0.4704 | Reaction Time (Hours) |
| Temp | 3 | 461.250925 | 153.750308 | 7.22 | 0.0205 | Temperature (Degrees Centigrade) |
The canonical analysis (Output 78.1.3) indicates that the predicted response surface is shaped like a saddle. The eigenvalue of 2.5 shows that the valley orientation of the saddle is less curved than the hill orientation, with an eigenvalue of  . The coefficients of the associated eigenvectors show that the valley is more aligned with Time and the hill with Temp. Because the canonical analysis resulted in a saddle point, the estimated surface does not have a unique optimum.
. The coefficients of the associated eigenvectors show that the valley is more aligned with Time and the hill with Temp. Because the canonical analysis resulted in a saddle point, the estimated surface does not have a unique optimum.
| Factor | Critical Value | Label | |
|---|---|---|---|
| Coded | Uncoded | ||
| Time | -0.441758 | 8.465935 | Reaction Time (Hours) |
| Temp | -0.309976 | 240.700718 | Temperature (Degrees Centigrade) |
| Predicted value at stationary point: 83.741940 | |||
| Eigenvalues | Eigenvectors | |
|---|---|---|
| Time | Temp | |
| 2.528816 | 0.953223 | -0.302267 |
| -9.996940 | 0.302267 | 0.953223 |
| Stationary point is a saddle point. | ||
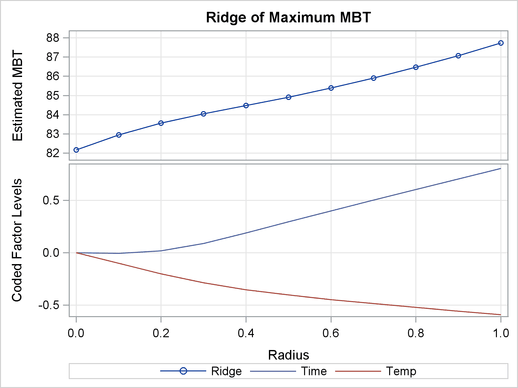
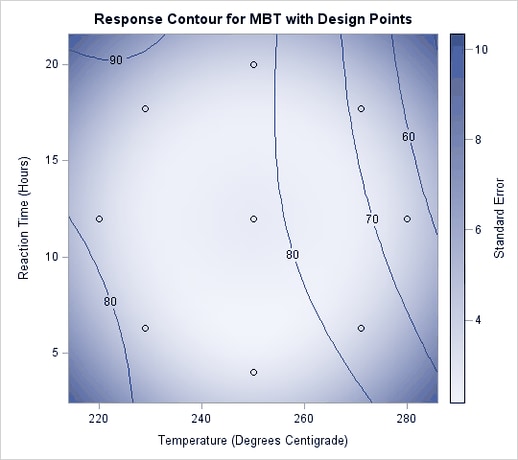
However, the ridge analysis in Output 78.1.4 and the ridge plot in Output 78.1.5 indicate that maximum yields result from relatively high reaction times and low temperatures. A contour plot of the predicted response surface, shown in Output 78.1.6, confirms this conclusion.
| Estimated Ridge of Maximum Response for Variable MBT: Percent Yield Mercaptobenzothiazole | ||||
|---|---|---|---|---|
| Coded Radius | Estimated Response | Standard Error | Uncoded Factor Values | |
| Time | Temp | |||
| 0.0 | 82.173110 | 2.665023 | 12.000000 | 250.000000 |
| 0.1 | 82.952909 | 2.648671 | 11.964493 | 247.002956 |
| 0.2 | 83.558260 | 2.602270 | 12.142790 | 244.023941 |
| 0.3 | 84.037098 | 2.533296 | 12.704153 | 241.396084 |
| 0.4 | 84.470454 | 2.457836 | 13.517555 | 239.435227 |
| 0.5 | 84.914099 | 2.404616 | 14.370977 | 237.919138 |
| 0.6 | 85.390012 | 2.410981 | 15.212247 | 236.624811 |
| 0.7 | 85.906767 | 2.516619 | 16.037822 | 235.449230 |
| 0.8 | 86.468277 | 2.752355 | 16.850813 | 234.344204 |
| 0.9 | 87.076587 | 3.130961 | 17.654321 | 233.284652 |
| 1.0 | 87.732874 | 3.648568 | 18.450682 | 232.256238 |