PROC RSREG: MODEL Statement :: SAS/STAT(R) 9.3 User's Guide

MODEL Statement

MODEL responses=independents </ options> ;

In the MODEL statement, you specify the response (dependent) variables followed by an equal sign and then the independent variables, some of which can be covariates.

Table 78.2 summarizes the options available in the MODEL statement. The statistic options specify which statistics are output to the OUT= data set. If none of the statistic options are selected, the data set is created but contains no observations. The statistic option keywords become values of the special variable _TYPE_ in the output data set.

Table 78.2 MODEL Statement Options
Task	Options
Analyze original data	NOCODE
Fit model to first BY group only	BYOUT
Declare covariates	COVAR=
Request additional statistics	PRESS
Request additional tests	LACKFIT
Suppress displayed output	NOANOVA
	NOOPTIMAL
	NOPRINT
Task	Statistic Options
Output statistics	ACTUAL
	PREDICT
	RESIDUAL
	L95
	U95
	L95M
	U95M
	D

The following list describes these options in alphabetical order.

ACTUAL

specifies that the observed response values from the input data set be written to the output data set.

BYOUT

uses only the first BY group to estimate the model. Subsequent BY groups have scoring statistics computed in the output data set only. The BYOUT option is used only when a BY statement is specified.

COVAR=n

declares that the first n variables on the right side of the model are simple linear regressors (covariates) and not factors in the quadratic response surface. By default, PROC RSREG forms quadratic and crossproduct effects for all regressor variables in the MODEL statement.

See the section Handling Covariates for more details and Example 78.2 for an example that uses covariates.

D

specifies that Cook’s 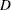$\text{[math]}$ influence statistic be written to the output data set.

See Chapter 4, Introduction to Regression Procedures, for details and formulas.

LACKFIT

performs a lack-of-fit test.

See Draper and Smith (1981) for a discussion of lack-of-fit tests.

L95

specifies that the lower bound of a 95% confidence interval for an individual predicted value be written to the output data set. The variance used in calculating this bound is a function of both the mean square error and the variance of the parameter estimates.

See Chapter 4, Introduction to Regression Procedures, for details and formulas.

L95M

specifies that the lower bound of a 95% confidence interval for the expected value of the dependent variable be written to the output data set. The variance used in calculating this bound is a function of the variance of the parameter estimates.

See Chapter 4, Introduction to Regression Procedures, for details and formulas.

NOANOVA

NOAOV

suppresses the display of the analysis of variance and parameter estimates from the model fit.

NOCODE

performs the canonical and ridge analyses with the parameter estimates derived from fitting the response to the original values of the factor variables, rather than their coded values (see the section Coding the Factor Variables for more details). Use this option if the data are already stored in a coded form.

NOOPTIMAL

NOOPT

suppresses the display of the canonical analysis for the quadratic response surface.

NOPRINT

suppresses the display of both the analysis of variance and the canonical analysis.

PREDICT

specifies that the values predicted by the model be written to the output data set.

PRESS

computes and displays the predicted residual sum of squares (PRESS) statistic for each dependent variable in the model. The PRESS statistic is added to the summary information at the beginning of the analysis of variance, so if the NOANOVA or NOPRINT option is specified, then the PRESS option has no effect.

See Chapter 4, Introduction to Regression Procedures, for details and formulas.

RESIDUAL

specifies that the residuals, calculated as ACTUAL $\text{[math]}$ PREDICTED, be written to the output data set.

U95

specifies that the upper bound of a 95% confidence interval for an individual predicted value be written to the output data set. The variance used in calculating this bound is a function of both the mean square error and the variance of the parameter estimates.

See Chapter 4, Introduction to Regression Procedures, for details and formulas.

U95M

specifies that the upper bound of a 95% confidence interval for the expected value of the dependent variable be written to the output data set. The variance used in calculating this bound is a function of the variance of the parameter estimates.

See Chapter 4, Introduction to Regression Procedures, for details and formulas.

The RSREG Procedure