The RSREG Procedure
| Computational Method |
Canonical Analysis
For each response variable, the model can be written in the form
 |
where
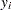
is the
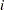th observation of the response variable. 
are the 
factor variables for the 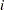th observation. 
are the 
covariates, including the intercept term.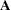 
is the
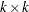symmetrized matrix of quadratic parameters, with diagonal elements equal to the coefficients of the pure quadratic terms in the model and off-diagonal elements equal to half the coefficient of the corresponding crossproduct.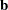 
is the
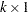vector of linear parameters. 
is the
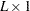vector of covariate parameters, one of which is the intercept.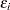 
is the error associated with the
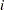th observation. Tests performed by PROC RSREG assume that errors are independently and normally distributed with mean zero and variance 
.
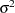The parameters in 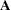, , 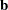and are estimated by least squares. To optimize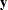 
with respect to 
, take partial derivatives, set them to zero, and solve:
 |
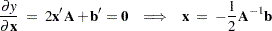You can determine if the solution is a maximum or minimum by looking at the eigenvalues of :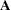
If the eigenvalues... |
then the solution is... |
|
|---|---|---|
are all negative |
a maximum |
|
are all positive |
a minimum |
|
have mixed signs |
a saddle point |
|
contain zeros |
in a flat area |
Ridge Analysis
If the largest eigenvalue is positive, its eigenvector gives the direction of steepest ascent from the stationary point; if the largest eigenvalue is negative, its eigenvector gives the direction of steepest descent. The eigenvectors corresponding to small or zero eigenvalues point in directions of relative flatness.
The point on the optimum response ridge at a given radius 
from the ridge origin is found by optimizing
 |
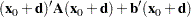over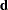 
satisfying 
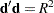, where 
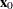is the 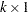vector containing the ridge origin 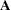and and 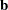are as previously discussed. By the method of Lagrange multipliers, the optimal 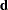has the form
 |
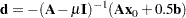where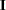 
is the 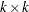identity matrix and 
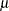is chosen so that 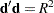. There can be several values of 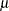that satisfy this constraint; the correct one depends on which sort of response ridge is of interest. If you are searching for the ridge of maximum response, then the appropriate 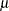is the unique one that satisfies the constraint and is greater than all the eigenvalues of 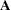. Similarly, the appropriate 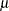for the ridge of minimum response satisfies the constraint and is less than all the eigenvalues of 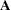. (See Myers and Montgomery (1995) for details.)