The QUANTREG Procedure
Example 75.5 Quantile Polynomial Regression for Salary Data
This example uses the data set from a university union survey of salaries of professors in 1991. The survey covered departments in U.S. colleges and universities that list programs in statistics. The goal here is to examine the relationship between faculty salaries and years of service.
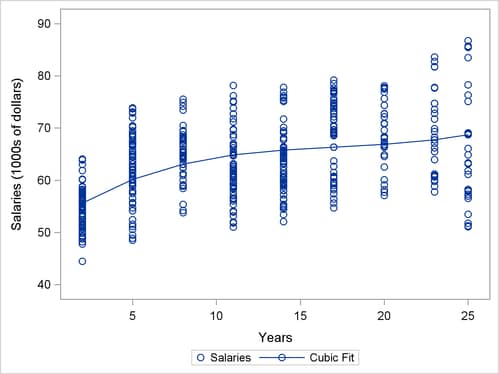
The data include salaries and years of service for 459 professors. The scatter plot in Output 75.5.1 shows that the relationship is not linear, and a quadratic or cubic regression curve is appropriate. Output 75.5.1 shows a cubic curve.
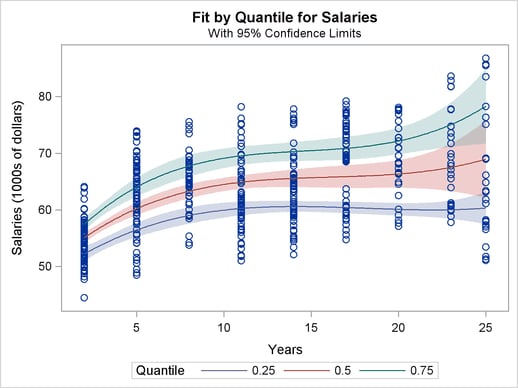
The curve in Output 75.5.1 does not adequately describe the conditional salary distributions and how they change with length of service. Output 75.5.2 shows the 25th, 50th, and 75th percentiles for each number of years, which gives a better picture of the conditional distributions.
data salary; input Salaries Years @@; label Salaries='Salaries (1000s of dollars)'; datalines; 54.94 2 58.24 2 58.11 2 52.23 2 52.98 2 57.62 2 44.48 2 57.22 2 54.24 2 54.79 2 56.42 2 61.90 2 63.90 2 64.10 2 47.77 2 54.86 2 49.31 2 53.37 2 51.69 2 53.66 2 58.77 2 56.77 2 53.06 2 54.86 2 ... more lines ... 85.72 25 64.87 25 51.76 25 51.11 25 51.31 25 78.28 25 57.91 25 86.78 25 58.27 25 56.56 25 76.33 25 61.83 25 69.13 25 63.15 25 66.13 25 ;
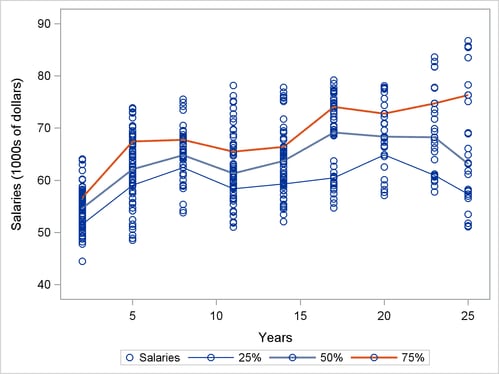
These descriptive percentiles do not clearly show trends with length of service. The following statements use the QUANTREG procedure to obtain a smooth version by using polynomial quantile regression. The results are shown in Output 75.5.3 and Output 75.5.5.
ods graphics on;
proc quantreg data=salary ci=sparsity;
model salaries = years years*years years*years*years
/quantile=0.25 0.5 0.75
plot=fitplot(showlimits);
test years/QINTERACT;
run;
Output 75.5.3 displays the regression coefficients for the three quantiles, from which you can see that there is a difference among the estimated parameters of the variable years across the three quantiles. To test whether the difference is significant, you can specify the option QINTERACT in the TEST statement. Output 75.5.4 indicates that the difference is not significant with the p-value greater than 0.05.
| BMI Percentiles for Men: 2-80 Years Old |
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 48.2509 | 1.3484 | 45.6011 | 50.9007 | 35.78 | <.0001 |
| Years | 1 | 2.2234 | 0.5455 | 1.1514 | 3.2953 | 4.08 | <.0001 |
| Years*Years | 1 | -0.1292 | 0.0500 | -0.2275 | -0.0308 | -2.58 | 0.0101 |
| Years*Years*Years | 1 | 0.0024 | 0.0013 | -0.0001 | 0.0049 | 1.86 | 0.0634 |
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 50.2512 | 1.2812 | 47.7334 | 52.7690 | 39.22 | <.0001 |
| Years | 1 | 2.7173 | 0.5947 | 1.5485 | 3.8860 | 4.57 | <.0001 |
| Years*Years | 1 | -0.1632 | 0.0632 | -0.2873 | -0.0390 | -2.58 | 0.0101 |
| Years*Years*Years | 1 | 0.0034 | 0.0018 | -0.0002 | 0.0070 | 1.85 | 0.0647 |
| Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | t Value | Pr > |t| | |
| Intercept | 1 | 51.0298 | 1.5886 | 47.9078 | 54.1517 | 32.12 | <.0001 |
| Years | 1 | 3.6513 | 0.7594 | 2.1590 | 5.1436 | 4.81 | <.0001 |
| Years*Years | 1 | -0.2390 | 0.0764 | -0.3892 | -0.0888 | -3.13 | 0.0019 |
| Years*Years*Years | 1 | 0.0055 | 0.0021 | 0.0013 | 0.0096 | 2.60 | 0.0098 |
| Test Results Equal Coefficients Across Quantiles |
||
|---|---|---|
| Chi-Square | DF | Pr > ChiSq |
| 3.4026 | 2 | 0.1825 |
The three fitted quantile curves with 95% confidence limits in the Output 75.5.5 clearly show that salary dispersion increases gradually with length of service. After 15 years, a salary over $70,000 is relatively high, while a salary less than $60,000 is relatively low. Percentile curves of this type are useful in medical science as reference curves; see Yu, Lu, and Stabder (2003).