The QUANTREG Procedure
| PROC QUANTREG Statement |
The PROC QUANTREG statement invokes the procedure. You can specify the following options in the PROC QUANTREG statement.
- ALGORITHM=algorithm <( suboptions )>
-
specifies an algorthm to estimate the regression parameters. Three algorithms are available: simplex (SIMPLEX), interior point (INTERIOR), and smoothing (SMOOTH).
The default algorithm depends on the number of the observations
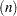 and the number of the covariates
and the number of the covariates 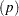 in the model estimation. See Table 75.1 for the relevant defaults.
in the model estimation. See Table 75.1 for the relevant defaults. Table 75.1 The Default Estimation Algorithm 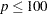
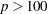
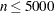
Simplex
Smoothing
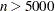
Interior point
Smoothing
Table 75.2 summarizes the options available for each of these methods.
Table 75.2 Options for Estimation Algorithms ALGORITHM= Value
Algorithm
Suboptions
SIMPLEX
Simplex
MAXSTATIONARY=
INTERIOR
Interior point
KAPPA= MAXIT= TOLERANCE=
SMOOTH
Smoothing
RRATIO=
With ALGORITHM=SIMPLEX you can specify the following suboption:
MAXSTATIONARY=m specifies that if the objective funtion has not improved for m consecutive iterations, the algorithm termintates. By default, m=1000.
With ALGORITHM=INTERIOR you can specify the following suboptions:
KAPPA=value specifies the step length parameter for the interior point algorithm. This parameter should be between 0 and 1. The larger the parameter, the faster the algorithm. However, numeric instability can occur as the parameter approaches 1. By default, KAPPA=0.99995. See the section Interior Point Algorithm for details.
MAXIT=m sets the maximum number of iterations for the interior point algorithm. By default, m=1000.
TOLERANCE=value specifies the tolerance for the convergence criterion of the interior point algorithm. The default value is 1E
 8. The QUANTREG procedure uses the duality gap as the convergence criterion. See the section Interior Point Algorithm for details.
8. The QUANTREG procedure uses the duality gap as the convergence criterion. See the section Interior Point Algorithm for details.
With the interior point algorithm, you can use the PERFORMANCE statement to enable parallel computing when multiple processors are available in the hardware.
With ALGORITHM=SMOOTH you can specify the following suboption:
RRATIO=value specifies the reduction ratio for the smoothing algorithm. This ratio is used for reducing the threshold of the smoothing algorithm. The value should be between 0 and 1. In theory, the smaller the reduction ration, the faster the smoothing algorithm. However, the optimal ratio is quite data dependent in practice. See the section Smoothing Algorithm for details.
- ALPHA=value
sets the confidence level for the confidence intervals for regression parameters. The value must be between 0 and 1. The default is ALPHA=0.05, corresponding to a 0.95 confidence interval.
- CI=NONE | RANK | SPARSITY<(BF | HS)></IID> | RESAMPLING<(NREP=n)>
-
specifies a method to compute confidence intervals for regression parameters. When you specify CI=SPARSITY or CI=RESAMPLING, the QUANTREG procedure also computes standard errors, t values, and p-values for regression parameters.
The following table summarizes these methods.
Table 75.3 Options for Confidence Intervals Value of CI=
Method
Additional Options
NONE
No confidence intervals computed
RANK
By inverting rank-score tests
SPARSITY
By estimating sparsity function
HS BF IID
RESAMPLING
By resampling
NREP
By default, when there are fewer than 5,000 observations, fewer than 20 variables in the data set, and the algorithm is simplex, the QUANTREG procedure computes confidence intervals by using the inverting rank-score test method; otherwise, the resampling method is used.
By default, confidence intervals are not computed for the quantile process, which is estimated when you specify the QUANTILE=PROCESS option in the MODEL statement. Confidence intervals for the quantile process are computed with the sparsity or resampling methods when you specify CI=SPARSITY or CI=RESAMPLING, respectively. The rank method for confidence intervals is not available with quantile processes because it is computationally prohibitive.
With the SPARSITY option, there are two suboptions for estimating the sparsity function. If you specify the IID suboption, the sparsity function is estimated by assuming that the errors in the linear model are independent and identically distributed (iid). By default, the sparsity function is estimated by assuming that the conditional quantile function is locally linear. See the section Sparsity for details. With both methods two bandwidth selection methods are available. You can specify the Bofinger method with the BF suboption or the Hall-Sheather method with the HS suboption. By default, the Hall-Sheather method is used.
With the RESAMPLING option, you can specify the number of repeats with the NREP=n suboption. By default, NREP=200. The value of n must be greater than 50.
- DATA=SAS-data-set
specifies the input SAS data set used by the QUANTREG procedure. By default, the most recently created SAS data set is used.
- INEST=SAS-data-set
specifies an input SAS data set that contains initial estimates for all the parameters in the model. The interior point algorithm and the smoothing algorithm use these estimates as a start. See the section INEST= Data Set for a detailed description of the contents of the INEST= data set.
- NAMELEN=n
specifies the length of effect names in tables and output data sets to be n characters, where n is a value between 20 and 200. The default length is 20 characters.
- ORDER=DATA | FORMATTED | FREQ | INTERNAL
-
specifies the order in which to sort the levels of the classification variables (which are specified in the CLASS statement). This option applies to the levels for all classification variables, except when you use the (default) ORDER=FORMATTED option with numeric classification variables that have no explicit format. With this option, the levels of such variables are ordered by their internal value.
The ORDER= option can take the following values:
Value of ORDER=
Levels Sorted By
DATA
Order of appearance in the input data set
FORMATTED
External formatted value, except for numeric variables with no explicit format, which are sorted by their unformatted (internal) value
FREQ
Descending frequency count; levels with the most observations come first in the order
INTERNAL
Unformatted value
By default, ORDER=FORMATTED. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine-dependent. For more information about sorting order, see the chapter on the SORT procedure in the Base SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.
- OUTEST=SAS-data-set
specifies an output SAS data set containing the parameter estimates for all quantiles. See the section OUTEST= Data Set for a detailed description of the contents of the OUTEST= data set.
- PLOT | PLOTS<(global-plot-options)> <=plot-request>
- PLOT | PLOTS<(global-plot-options)> <=(plot-request < ...plot-request > )>
-
specifies options that control details of the plots. These plots fall into two categories, diagnostic plots and fit plots. If you do not specify the PLOTS= option, PROC QUANTREG produces the quantile fit plot by default when a single continuous variable is specified in the model. You can use the PLOTS= option in the PROC statement to request various diagnostic plots. In addition to these two categories of plots, you can use the PLOT= option in the MODEL statement to request the quantile process plot for any effects specified in the model.
When you specify one plot-request, you can omit the parentheses around the plot request. Here are some examples:
plots=ddplot plots=(ddplot rdplot)
ODS Graphics must be enabled before requesting plots. For example:
ods graphics on; proc quantreg plots=fitplot; model y=x1; run; ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21, Statistical Graphics Using ODS.
The global-plot-options apply to all plots generated by the QUANTREG procedure. The following global plot option is available:
- MAXPOINTS=NONE | number
specifies that plots with elements that require processing more than number points be suppressed. The default is MAXPOINTS=5000. This cutoff is ignored if you specify MAXPOINTS=NONE.
- ONLY
suppresses the default quantile fit plot. Only plots specifically requested are displayed.
You can specify more than one plot request within the parentheses after PLOTS=. For a single plot request, you can omit the parentheses. The following plot requests are available.
- ALL
creates all appropriate plots.
- DDPLOT<(LABEL=ALL | LEVERAGE | NONE | OUTLIER)>
-
creates a plot of robust distance against Mahalanobis distance. See the section Leverage Point and Outlier Detection for details about robust distance. The LABEL= option specifies how the points on this plot are to be labeled, as summarized by the following table.
Table 75.4 Options for Label Value of LABEL=
Label Method
ALL
Label all points
LEVERAGE
Label leverage points
NONE
No labels
OUTLIERS
Label outliers
By default, the QUANTREG procedure labels both outliers and leverage points.
If you specify ID variables in the ID statement, the values of the first ID variable are used as labels; otherwise, observation numbers are used as labels.
- FITPLOT<(NOLIMITS | SHOWLIMITS | NODATA)>
creates a plot of fitted conditional quantiles against the single continuous variable that is specified in the model. This plot is produced only when the response is modeled as a function of a single continuous variable. Multiple lines or curves are drawn on this plot if you specify several quantiles with the QUANTILE= option in the MODEL statement. By default, confidence limits are added to the plot when a single quantile is requested, and the confidence limits are not shown on the plot when multiple quantiles are requested. The NOLIMITS option suppresses these limits. The SHOWLIMITS option adds these limits when multiple quantiles are requested. The NODATA option suppresses the observed data, which are superimposed on the plot by default.
- HISTOGRAM
creates a histogram for the standardized residuals based on the quantile regression estimates. The histogram is superimposed with a normal density curve and a kernel density curve.
- NONE
suppresses all plots.
- QQPLOT
creates the normal quantile-quantile plot for the standardized residuals based on the quantile regression estimates.
- RDPLOT<(LABEL=ALL | LEVERAGE | NONE | OUTLIER)>
-
creates the plot of standardized residual against robust distance. See the section Leverage Point and Outlier Detection for details about robust distance. The LABEL= option specifies a label method for points on this plot. These label methods are described in Table 75.4.
By default, the QUANTREG procedure labels both outliers and leverage points.
If you specify ID variables in the ID statement, the values of the first ID variable are used as labels; otherwise, observation numbers are used as labels.
- PP
requests preprocessing to speed up the interior point algorithm or the smoothing algorithm. The preprocessing uses a subsampling algorithm to reduce the original problem to a smaller one iteratively. It assumes that the data set is evenly distributed. Preprocessing should be used only for very large data sets, such as data sets with more than 100,000 observations. See Portnoy and Koenker (1997) for details.
