The PLM Procedure
Example 68.2 Working with Item Stores
This example demonstrates how procedures save statistical analysis context and results into item stores and how you can use PROC PLM to make post hoc inference based on saved item stores. The data are taken from McCullagh and Nelder (1989) and concern the effects on taste of various cheese additives. Four cheese additives were tested, and 52 response ratings for each additive were obtained. The response was measured on a scale of nine categories that range from strong dislike (1) to excellent taste (9). The following program saves the data in the data set Cheese. The variable y contains the taste rating, the variable Additive contains cheese additive types, and the variable freq contains the frequencies with which each additive received each rating.
data Cheese;
do Additive = 1 to 4;
do y = 1 to 9;
input freq @@;
output;
end;
end;
label y='Taste Rating';
datalines;
0 0 1 7 8 8 19 8 1
6 9 12 11 7 6 1 0 0
1 1 6 8 23 7 5 1 0
0 0 0 1 3 7 14 16 11
;
The response y is a categorical variable that contains nine ordered levels. You can use PROC LOGISTIC to fit an ordinal model to investigate the effects of the cheese additive types on taste ratings. Suppose you also want to save the ordinal model into an item store so that you can make statistical inference later. You can use the following statements to perform the tasks:
proc logistic data=cheese; freq freq; class additive y / param=glm; model y=additive; store sasuser.cheese; title 'Ordinal Model on Cheese Additives'; run;
By default, PROC LOGISTIC uses the cumulative logit model for the ordered categorical response. The STORE statement requests that the fitted model be saved to a SAS item store named sasuser.cheese. The name is a two-level SAS name of the form libname.membername. If libname is not specified in the STORE statement, the fitted results are saved in work.membername and the item store is deleted after the current SAS session ends. With this example, the fitted model is saved to an item store named sasuser.cheese in the SASUSER library. It is not deleted after the current SAS session ends. You can use PROC PLM to restore the results later.
The following statements use PROC PLM to load the saved model context and results by specifying SOURCE= with the target item store sasuser.cheese. Then they use two SHOW statements to display separate information saved in the item store. The first SHOW statement with the PROGRAM option displays the program that was used to generate the item store sasuser.cheese. The second SHOW statement with the PARMS option displays parameter estimates and associated statistics of the fitted ordinal model.
proc plm source=sasuser.cheese; show program; show parms; run;
Output 68.2.1 displays the program that generated the item store sasuser.cheese. Except for the title information, it matches the original program.
| Ordinal Model on Cheese Additives |
| SAS Program Information |
|---|
| proc logistic data=cheese; |
| freq freq; |
| class additive y / param=glm; |
| model y=additive; |
| store sasuser.cheese; |
| run; |
Output 68.2.2 displays estimates of the intercept terms and covariates and associated statistics. The intercept terms correspond to eight cumulative logits defined on taste ratings; that is, the  th intercept for
th intercept for  th logit is
th logit is
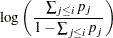 |
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | Taste Rating |
Estimate | Standard Error |
| Intercept | 1 | -7.0801 | 0.5624 |
| Intercept | 2 | -6.0249 | 0.4755 |
| Intercept | 3 | -4.9254 | 0.4272 |
| Intercept | 4 | -3.8568 | 0.3902 |
| Intercept | 5 | -2.5205 | 0.3431 |
| Intercept | 6 | -1.5685 | 0.3086 |
| Intercept | 7 | -0.06688 | 0.2658 |
| Intercept | 8 | 1.4930 | 0.3310 |
| Additive 1 | 1.6128 | 0.3778 | |
| Additive 2 | 4.9645 | 0.4741 | |
| Additive 3 | 3.3227 | 0.4251 | |
| Additive 4 | 0 | . | |
You can perform various statistical inference tasks from a saved item store, as long as the task is applicable under the model context. For example, you can perform group comparisons between different cheese additive types. See the next example for details.
