The FREQ Procedure
Example 36.4 Binomial Proportions
In this example, PROC FREQ computes binomial proportions, confidence limits, and tests. The example uses the eye and hair color data from Example 36.1. By default, PROC FREQ computes the binomial proportion as the proportion of observations in the first level of the one-way table. You can designate a different level by using the LEVEL= binomial-option.
The following PROC FREQ statements compute the proportion of children with brown eyes (from the data set in Example 36.1) and test the null hypothesis that the population proportion equals 50%. These statements also compute an equivalence for the proportion of children with fair hair.
The first TABLES statement requests a one-way frequency table for the variable Eyes. The BINOMIAL option requests the binomial proportion, confidence limits, and test. PROC FREQ computes the proportion with Eyes = 'brown', which is the first level displayed in the table. The AC, WILSON, and EXACT binomial-options request the following confidence limits types: Agresti-Coull, Wilson (score), and exact (Clopper-Pearson). By default, PROC FREQ provides Wald and exact (Clopper-Pearson) confidence limits for the binomial proportion. The BINOMIAL option also produces an asymptotic Wald test that the proportion equals 0.5. You can specify a different test proportion with the P= binomial-option. The ALPHA=0.1 option specifies that 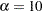 %, which produces
%, which produces  % confidence limits.
% confidence limits.
The second TABLES statement requests a one-way frequency table for the variable Hair. The BINOMIAL option requests the proportion for the first level, Hair = 'fair'. The EQUIV binomial-option requests an equivalence test for the binomial proportion. The P=.28 option specifies 0.28 as the null hypothesis proportion, and the MARGIN=.1 option specifies 0.1 as the equivalence test margin.
proc freq data=Color order=freq; tables Eyes / binomial(ac wilson exact) alpha=.1; tables Hair / binomial(equiv p=.28 margin=.1); weight Count; title 'Hair and Eye Color of European Children'; run;
Output 36.4.1 displays the results for eye color, and Output 36.4.2 displays the results for hair color.
| Hair and Eye Color of European Children |
| Eye Color | ||||
|---|---|---|---|---|
| Eyes | Frequency | Percent | Cumulative Frequency |
Cumulative Percent |
| brown | 341 | 44.75 | 341 | 44.75 |
| blue | 222 | 29.13 | 563 | 73.88 |
| green | 199 | 26.12 | 762 | 100.00 |
| Binomial Proportion for Eyes = brown |
|
|---|---|
| Proportion | 0.4475 |
| ASE | 0.0180 |
| Type | 90% Confidence Limits | |
|---|---|---|
| Wilson | 0.4181 | 0.4773 |
| Agresti-Coull | 0.4181 | 0.4773 |
| Clopper-Pearson (Exact) | 0.4174 | 0.4779 |
| Test of H0: Proportion = 0.5 | |
|---|---|
| ASE under H0 | 0.0181 |
| Z | -2.8981 |
| One-sided Pr < Z | 0.0019 |
| Two-sided Pr > |Z| | 0.0038 |
The frequency table in Output 36.4.1 displays the values of Eyes in order of descending frequency count. PROC FREQ computes the proportion of children in the first level displayed in the frequency table, Eyes = 'brown'. Output 36.4.1 displays the binomial proportion confidence limits and test. The confidence limits are  % confidence limits. If you do not specify the ALPHA= option, PROC FREQ computes
% confidence limits. If you do not specify the ALPHA= option, PROC FREQ computes 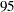 % confidence limits by default. Because the value of
% confidence limits by default. Because the value of 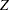 is less than zero, PROC FREQ displays the a left-sided
is less than zero, PROC FREQ displays the a left-sided  -value (0.0019). This small
-value (0.0019). This small  -value supports the alternative hypothesis that the true value of the proportion of children with brown eyes is less than 50%.
-value supports the alternative hypothesis that the true value of the proportion of children with brown eyes is less than 50%.
Output 36.4.2 displays the equivalence test results produced by the second TABLES statement. The null hypothesis proportion is 0.28 and the equivalence margins are –0.1 and 0.1, which yield equivalence limits of 0.18 and 0.38. PROC FREQ provides two one-sided tests (TOST) for equivalence. The small  -value indicates rejection of the null hypothesis in favor of the alternative that the proportion is equivalent to the null value.
-value indicates rejection of the null hypothesis in favor of the alternative that the proportion is equivalent to the null value.
| Hair Color | ||||
|---|---|---|---|---|
| Hair | Frequency | Percent | Cumulative Frequency |
Cumulative Percent |
| fair | 228 | 29.92 | 228 | 29.92 |
| medium | 217 | 28.48 | 445 | 58.40 |
| dark | 182 | 23.88 | 627 | 82.28 |
| red | 113 | 14.83 | 740 | 97.11 |
| black | 22 | 2.89 | 762 | 100.00 |
| Equivalence Analysis | |
|---|---|
| H0: P - p0 <= Lower Margin or >= Upper Margin | |
| Ha: Lower Margin < P - p0 < Upper Margin | |
| p0 = 0.28 Lower Margin = -0.1 Upper Margin = 0.1 | |
| Proportion | ASE (Sample) |
| 0.2992 | 0.0166 |
| Two One-Sided Tests (TOST) | |||
|---|---|---|---|
| Test | Z | P-Value | |
| Lower Margin | 7.1865 | Pr > Z | <.0001 |
| Upper Margin | -4.8701 | Pr < Z | <.0001 |
| Overall | <.0001 | ||
| Equivalence Limits | 90% Confidence Limits | ||
|---|---|---|---|
| 0.1800 | 0.3800 | 0.2719 | 0.3265 |
