Evaluating the Effects of Ties
Previous Page | Next Page

The CLUSTER Procedure

 

Example 30.4 Evaluating the Effects of Ties

If, at some level of the cluster history, there is a tie for minimum distance between clusters, then one or more levels of the sample cluster tree are not uniquely determined. This example shows how the degree of indeterminacy can be assessed.

Mammals have four kinds of teeth: incisors, canines, premolars, and molars. The following data set gives the number of teeth of each kind on one side of the top and bottom jaws for 32 mammals.

Since all eight variables are measured in the same units, it is not strictly necessary to rescale the data. However, the canines have much less variance than the other kinds of teeth and, therefore, have little effect on the analysis if the variables are not standardized. An average linkage cluster analysis is run with and without standardization to enable comparison of the results. 

title 'Hierarchical Cluster Analysis of Mammals'' Teeth Data';
title2 'Evaluating the Effects of Ties';
data teeth;
   input Mammal & $16. v1-v8 @@;
   label v1='Top incisors'
         v2='Bottom incisors'
         v3='Top canines'
         v4='Bottom canines'
         v5='Top premolars'
         v6='Bottom premolars'
         v7='Top molars'
         v8='Bottom molars';
   datalines;
Brown Bat         2 3 1 1 3 3 3 3   Mole              3 2 1 0 3 3 3 3
Silver Hair Bat   2 3 1 1 2 3 3 3   Pigmy Bat         2 3 1 1 2 2 3 3
House Bat         2 3 1 1 1 2 3 3   Red Bat           1 3 1 1 2 2 3 3
Pika              2 1 0 0 2 2 3 3   Rabbit            2 1 0 0 3 2 3 3
Beaver            1 1 0 0 2 1 3 3   Groundhog         1 1 0 0 2 1 3 3
Gray Squirrel     1 1 0 0 1 1 3 3   House Mouse       1 1 0 0 0 0 3 3
Porcupine         1 1 0 0 1 1 3 3   Wolf              3 3 1 1 4 4 2 3
Bear              3 3 1 1 4 4 2 3   Raccoon           3 3 1 1 4 4 3 2
Marten            3 3 1 1 4 4 1 2   Weasel            3 3 1 1 3 3 1 2
Wolverine         3 3 1 1 4 4 1 2   Badger            3 3 1 1 3 3 1 2
River Otter       3 3 1 1 4 3 1 2   Sea Otter         3 2 1 1 3 3 1 2
Jaguar            3 3 1 1 3 2 1 1   Cougar            3 3 1 1 3 2 1 1
Fur Seal          3 2 1 1 4 4 1 1   Sea Lion          3 2 1 1 4 4 1 1
Grey Seal         3 2 1 1 3 3 2 2   Elephant Seal     2 1 1 1 4 4 1 1
Reindeer          0 4 1 0 3 3 3 3   Elk               0 4 1 0 3 3 3 3
Deer              0 4 0 0 3 3 3 3   Moose             0 4 0 0 3 3 3 3
;


The following statements produce Output 30.4.1: 

title3 'Raw Data';
proc cluster data=teeth method=average nonorm noeigen;
   var v1-v8;
   id mammal;
run;

Output 30.4.1 Average Linkage Analysis of Mammals’ Teeth Data: Raw Data
Hierarchical Cluster Analysis of Mammals' Teeth Data
Evaluating the Effects of Ties
Raw Data

The CLUSTER Procedure
Average Linkage Cluster Analysis

Root-Mean-Square Total-Sample Standard Deviation 0.898027

Cluster History
Number
of
Clusters		 Clusters Joined Freq RMS
Distance		 Tie
31 Beaver Groundhog 2 0 T
30 Gray Squirrel Porcupine 2 0 T
29 Wolf Bear 2 0 T
28 Marten Wolverine 2 0 T
27 Weasel Badger 2 0 T
26 Jaguar Cougar 2 0 T
25 Fur Seal Sea Lion 2 0 T
24 Reindeer Elk 2 0 T
23 Deer Moose 2 0  
22 Brown Bat Silver Hair Bat 2 1 T
21 Pigmy Bat House Bat 2 1 T
20 Pika Rabbit 2 1 T
19 CL31 CL30 4 1 T
18 CL28 River Otter 3 1 T
17 CL27 Sea Otter 3 1 T
16 CL24 CL23 4 1  
15 CL21 Red Bat 3 1.2247  
14 CL17 Grey Seal 4 1.291  
13 CL29 Raccoon 3 1.4142 T
12 CL25 Elephant Seal 3 1.4142  
11 CL18 CL14 7 1.5546  
10 CL22 CL15 5 1.5811  
9 CL20 CL19 6 1.8708 T
8 CL11 CL26 9 1.9272  
7 CL8 CL12 12 2.2278  
6 Mole CL13 4 2.2361  
5 CL9 House Mouse 7 2.4833  
4 CL6 CL7 16 2.5658  
3 CL10 CL16 9 2.8107  
2 CL3 CL5 16 3.7054  
1 CL2 CL4 32 4.2939  


The following statements produce Output 30.4.2: 

title3 'Standardized Data';
proc cluster data=teeth std method=average nonorm noeigen;
   var v1-v8;
   id mammal;
run;

Output 30.4.2 Average Linkage Analysis of Mammals’ Teeth Data: Standardized Data
Hierarchical Cluster Analysis of Mammals' Teeth Data
Evaluating the Effects of Ties
Standardized Data

The CLUSTER Procedure
Average Linkage Cluster Analysis


The data have been standardized to mean 0 and variance 1

Root-Mean-Square Total-Sample Standard Deviation 1

Cluster History
Number
of
Clusters		 Clusters Joined Freq RMS
Distance		 Tie
31 Beaver Groundhog 2 0 T
30 Gray Squirrel Porcupine 2 0 T
29 Wolf Bear 2 0 T
28 Marten Wolverine 2 0 T
27 Weasel Badger 2 0 T
26 Jaguar Cougar 2 0 T
25 Fur Seal Sea Lion 2 0 T
24 Reindeer Elk 2 0 T
23 Deer Moose 2 0  
22 Pigmy Bat Red Bat 2 0.9157  
21 CL28 River Otter 3 0.9169  
20 CL31 CL30 4 0.9428 T
19 Brown Bat Silver Hair Bat 2 0.9428 T
18 Pika Rabbit 2 0.9428  
17 CL27 Sea Otter 3 0.9847  
16 CL22 House Bat 3 1.1437  
15 CL21 CL17 6 1.3314  
14 CL25 Elephant Seal 3 1.3447  
13 CL19 CL16 5 1.4688  
12 CL15 Grey Seal 7 1.6314  
11 CL29 Raccoon 3 1.692  
10 CL18 CL20 6 1.7357  
9 CL12 CL26 9 2.0285  
8 CL24 CL23 4 2.1891  
7 CL9 CL14 12 2.2674  
6 CL10 House Mouse 7 2.317  
5 CL11 CL7 15 2.6484  
4 CL13 Mole 6 2.8624  
3 CL4 CL8 10 3.5194  
2 CL3 CL6 17 4.1265  
1 CL2 CL5 32 4.7753  

There are ties at 16 levels for the raw data but at only 10 levels for the standardized data. There are more ties for the raw data because the increments between successive values are the same for all of the raw variables but different for the standardized variables.

One way to assess the importance of the ties in the analysis is to repeat the analysis on several random permutations of the observations and then to see to what extent the results are consistent at the interesting levels of the cluster history. Three macros are presented to facilitate this process, as follows. 

/* --------------------------------------------------------- */
/*                                                           */
/* The macro CLUSPERM randomly permutes observations and     */
/* does a cluster analysis for each permutation.             */
/* The arguments are as follows:                             */
/*                                                           */
/*    data    data set name                                  */
/*    var     list of variables to cluster                   */
/*    id      id variable for proc cluster                   */
/*    method  clustering method (and possibly other options) */
/*    nperm   number of random permutations.                 */
/*                                                           */
/* --------------------------------------------------------- */
%macro CLUSPERM(data,var,id,method,nperm);

   /* ------CREATE TEMPORARY DATA SET WITH RANDOM NUMBERS------ */
   data _temp_;
      set &data;
      array _random_ _ran_1-_ran_&nperm;
      do over _random_;
        _random_=ranuni(835297461);
      end;
   run;

   /* ------PERMUTE AND CLUSTER THE DATA----------------------- */
   %do n=1 %to &nperm;
       proc sort data=_temp_(keep=_ran_&n &var &id) out=_perm_;
          by _ran_&n;
       run;

       proc cluster method=&method noprint outtree=_tree_&n;
          var &var;
          id &id;
       run;
   %end;
%mend;



/* --------------------------------------------------------- */
/*                                                           */
/* The macro PLOTPERM plots various cluster statistics       */
/* against the number of clusters for each permutation.      */
/* The arguments are as follows:                             */
/*                                                           */
/*    nclus   maximum number of clusters to be plotted       */
/*    nperm   number of random permutations.                 */
/*                                                           */
/* --------------------------------------------------------- */
%macro PLOTPERM(nclus,nperm);

   /* ---CONCATENATE TREE DATA SETS FOR 20 OR FEWER CLUSTERS--- */
   data _plot_;
      set %do n=1 %to &nperm; _tree_&n(in=_in_&n) %end;;
      if _ncl_<=&nclus;
      %do n=1 %to &nperm;
         if _in_&n then _perm_=&n;
      %end;
      label _perm_='permutation number';
      keep _ncl_ _psf_ _pst2_ _ccc_ _perm_;
   run;

   /* ---PLOT THE REQUESTED STATISTICS BY NUMBER OF CLUSTERS--- */
   proc sgscatter;
      compare y=(_ccc_ _psf_ _pst2_) x=_ncl_ /group=_perm_;
      label _ccc_ = 'CCC' _psf_ = 'Pseudo F' _pst2_ = 'Pseudo T-Squared';
   run;
%mend;

/* --------------------------------------------------------- */
/*                                                           */
/* The macro TABPERM generates cluster-membership variables  */
/* for a specified number of clusters for each permutation.  */
/* PROC TABULATE gives the frequencies and means.            */
/* The arguments are as follows:                             */
/*                                                           */
/*    var     list of variables to cluster                   */
/*            (no "-" or ":" allowed)                        */
/*    id      id variable for proc cluster                   */
/*    meanfmt format for printing means in PROC TABULATE     */
/*    nclus   number of clusters desired                     */
/*    nperm   number of random permutations.                 */
/*                                                           */
/* --------------------------------------------------------- */
%macro TABPERM(var,id,meanfmt,nclus,nperm);

   /* ------CREATE DATA SETS GIVING CLUSTER MEMBERSHIP--------- */
   %do n=1 %to &nperm;
      proc tree data=_tree_&n noprint n=&nclus
                out=_out_&n(drop=clusname
                              rename=(cluster=_clus_&n));
         copy &var;
         id &id;
      run;

      proc sort;
         by &id &var;
      run;
   %end;

   /* ------MERGE THE CLUSTER VARIABLES------------------------ */
   data _merge_;
      merge
         %do n=1 %to &nperm;
            _out_&n
         %end;;
      by &id &var;
      length all_clus $ %eval(3*&nperm);
      %do n=1 %to &nperm;
         substr( all_clus, %eval(1+(&n-1)*3), 3) =
            put( _clus_&n, 3.);
      %end;
   run;

   /* ------ TABULATE CLUSTER COMBINATIONS------------ */
   proc sort;
      by _clus_:;
   run;
   proc tabulate order=data formchar='           ';
      class all_clus;
      var &var;
      table all_clus, n='FREQ'*f=5. mean*f=&meanfmt*(&var) /
         rts=%eval(&nperm*3+1);
   run;
%mend;

To use these macros, it is first convenient to define a macro variable, VLIST, listing the teeth variables, since the forms V1-V8 or V: cannot be used with the TABULATE procedure in the TABPERM macro: 

/* -TABULATE does not accept hyphens or colons in VAR lists- */
%let vlist=v1 v2 v3 v4 v5 v6 v7 v8;

The CLUSPERM macro is then called to analyze 10 random permutations. The PLOTPERM macro plots the pseudo F and 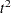statistics and the cubic clustering criterion. Since the data are discrete, the pseudo F statistic and the cubic clustering criterion can be expected to increase as the number of clusters increases, so local maxima or large jumps in these statistics are more relevant than the global maximum in determining the number of clusters. For the raw data, only the pseudo 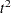statistic indicates the possible presence of clusters, with the four-cluster level being suggested. Hence, the macros are used as follows to analyze the results at the four-cluster level: 

title3 'Raw Data';

/* ------CLUSTER RAW DATA WITH AVERAGE LINKAGE-------------- */
%clusperm( teeth, &vlist, mammal, average, 10);


The following statements produce Output 30.4.3. 

/* -----PLOT STATISTICS FOR THE LAST 20 LEVELS-------------- */
%plotperm(20, 10);

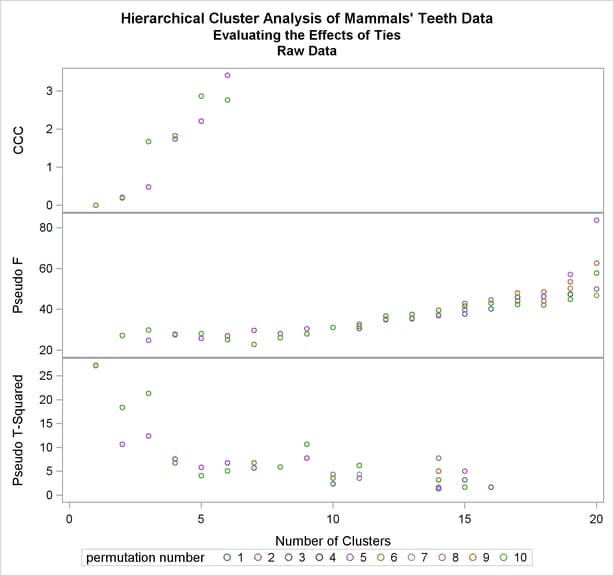
Output 30.4.3 Analysis of 10 Random Permutations of Raw Mammals’ Teeth Data
Analysis of 10 Random Permutations of Raw Mammals’ Teeth Data

The following statements produce Output 30.4.4. 

/* ------ANALYZE THE 4-CLUSTER LEVEL------------------------ */
%tabperm( &vlist, mammal, 9.1, 4, 10);

Output 30.4.4 Raw Mammals’ Teeth Data: Indeterminacy at the Four-Cluster Level
Hierarchical Cluster Analysis of Mammals' Teeth Data
Evaluating the Effects of Ties
Raw Data

  FREQ Mean
Top incisors Bottom incisors Top canines Bottom canines Top premolars Bottom premolars Top molars Bottom molars
all_clus 4 0.0 4.0 0.5 0.0 3.0 3.0 3.0 3.0
1 3 1 1 1 3 3 3 2 3
2 2 2 2 2 2 1 2 1 1 15 2.9 2.6 1.0 1.0 3.6 3.4 1.3 1.8
2 4 2 2 4 2 1 2 1 1 1 3.0 2.0 1.0 0.0 3.0 3.0 3.0 3.0
3 1 3 3 3 1 2 1 3 2 5 1.0 1.0 0.0 0.0 1.2 0.8 3.0 3.0
3 4 3 3 4 1 2 1 3 2 2 2.0 1.0 0.0 0.0 2.5 2.0 3.0 3.0
4 4 4 4 4 4 4 4 4 4 5 1.8 3.0 1.0 1.0 2.0 2.4 3.0 3.0


From the TABULATE output, you can see that two types of clustering are obtained. In one case, the mole is grouped with the carnivores, while the pika and rabbit are grouped with the rodents. In the other case, both the mole and the lagomorphs are grouped with the bats.

Next, the analysis is repeated with the standardized data as shown in the following statements. The pseudo F and 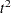statistics indicate three or four clusters, while the cubic clustering criterion shows a sharp rise up to four clusters and then levels off up to six clusters. So the TABPERM macro is used again at the four-cluster level. In this case, there is no indeterminacy, because the same four clusters are obtained with every permutation, although in different orders. It must be emphasized, however, that lack of indeterminacy in no way indicates validity. 

title3 'Standardized Data';

/*------CLUSTER STANDARDIZED DATA WITH AVERAGE LINKAGE------*/
%clusperm( teeth, &vlist, mammal, average std, 10);

The following statements produce Output 30.4.5. 

/* -----PLOT STATISTICS FOR THE LAST 20 LEVELS-------------- */
%plotperm(20, 10);

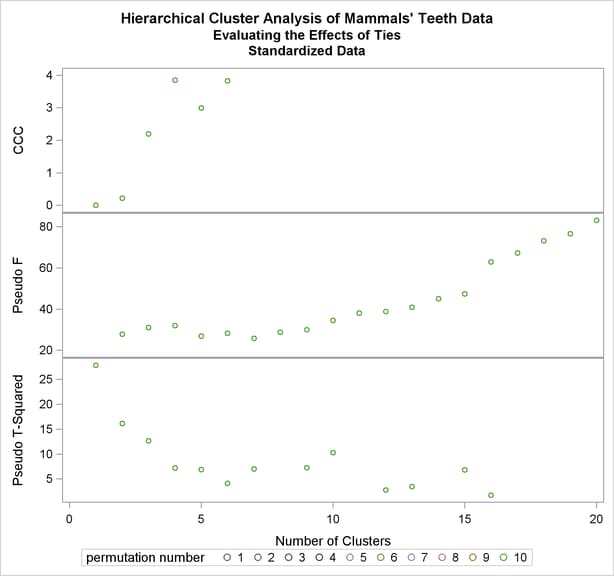
Output 30.4.5 Analysis of 10 Random Permutations of Standardized Mammals’ Teeth Data
Analysis of 10 Random Permutations of Standardized Mammals’ Teeth Data


The following statements produce Output 30.4.6. 

/* ------ANALYZE THE 4-CLUSTER LEVEL------------------------ */
%tabperm( &vlist, mammal, 9.1, 4, 10);

Output 30.4.6 Standardized Mammals’ Teeth Data: No Indeterminacy at the Four-Cluster Level
Hierarchical Cluster Analysis of Mammals' Teeth Data
Evaluating the Effects of Ties
Standardized Data

  FREQ Mean
Top incisors Bottom incisors Top canines Bottom canines Top premolars Bottom premolars Top molars Bottom molars
all_clus 4 0.0 4.0 0.5 0.0 3.0 3.0 3.0 3.0
1 3 1 1 1 3 3 3 2 3
2 2 2 2 2 2 1 2 1 1 15 2.9 2.6 1.0 1.0 3.6 3.4 1.3 1.8
3 1 3 3 3 1 2 1 3 2 7 1.3 1.0 0.0 0.0 1.6 1.1 3.0 3.0
4 4 4 4 4 4 4 4 4 4 6 2.0 2.8 1.0 0.8 2.2 2.5 3.0 3.0

Previous Page | Next Page | Top of Page
Copyright © SAS Institute Inc. All rights reserved.