The CLUSTER Procedure
| Ultrametrics |
A dissimilarity measure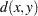 
is called an ultrametric if it satisfies the following conditions:
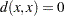for all x 
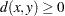for all x, y 
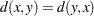for all x, y 
for all x, y, and z
Any hierarchical clustering method induces a dissimilarity measure on the observations—say,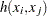 
. Let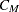 
be the cluster with the fewest members that contains both 
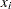and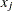 
. Assume 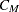was formed by joining 
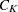and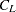 
. Then define 
.
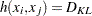If the fusion of 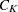and 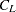reduces the number of clusters from g to 
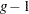, then define 
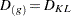. Johnson (1967) shows that if
 |
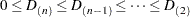then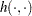 
is an ultrametric. A method that always satisfies this condition is said to be a monotonic or ultrametric clustering method. All methods implemented in PROC CLUSTER except CENTROID, EML, and MEDIAN are ultrametric (Milligan; 1979; Batagelj; 1981).