The CLUSTER Procedure

The root mean squared standard deviation of a cluster 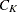is

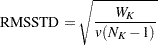The R-square statistic for a given level of the hierarchy is

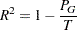The squared semipartial correlation for joining clusters 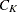and is

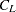The bimodality coefficient is

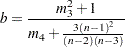where 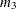is skewness and 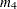is kurtosis. Values of b greater than 0.555 (the value for a uniform population) can indicate bimodal or multimodal marginal distributions. The maximum of 1.0 (obtained for the Bernoulli distribution) is obtained for a population with only two distinct values. Very heavy-tailed distributions have small values of b regardless of the number of modes.

Formulas for the cubic-clustering criterion and approximate expected R square are given in Sarle (1983).

The pseudo F statistic for a given level is

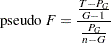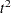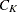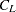The pseudo statistic for joining and is

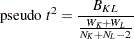The pseudo F and 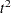statistics can be useful indicators of the number of clusters, but they are not distributed as F and 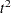random variables. If the data are independently sampled from a multivariate normal distribution with a scalar covariance matrix and if the clustering method allocates observations to clusters randomly (which no clustering method actually does), then the pseudo F statistic is distributed as an F random variable with 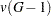and 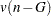degrees of freedom. Under the same assumptions, the pseudo 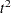statistic is distributed as an F random variable with v and 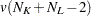degrees of freedom. The pseudo 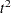statistic differs computationally from Hotelling’s 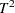in that the latter uses a general symmetric covariance matrix instead of a scalar covariance matrix. The pseudo F statistic was suggested by Calinski and Harabasz (1974). The pseudo 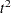statistic is related to the 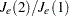statistic of Duda and Hart (1973) by

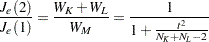See Milligan and Cooper (1985) and Cooper and Milligan (1988) regarding the performance of these statistics in estimating the number of population clusters. Conservative tests for the number of clusters using the pseudo F and 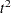statistics can be obtained by the Bonferroni approach (Hawkins, Muller, and ten Krooden; 1982, pp. 337–340).