| The SEQDESIGN Procedure |
| Applicable Regression Parameter Tests and Sample Size Computation |
The SEQDESIGN procedure provides sample size computation for tests of a regression parameter in three regression models: normal regression, logistic regression, and proportional hazards regression.
To test a parameter 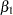 in a regression model, the variance of the parameter estimate
in a regression model, the variance of the parameter estimate 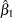 is needed for the sample size computation. In a simple regression model with one covariate X1, the variance of
is needed for the sample size computation. In a simple regression model with one covariate X1, the variance of 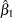 is inversely related to the variance of X1,
is inversely related to the variance of X1, 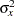 . That is,
. That is,
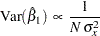 |
for the normal regression and logistic regression models, where 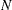 is the sample size, and
is the sample size, and
 |
for the proportional hazards regression model, where 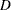 is the number of events.
is the number of events.
For a regression model with more than one covariate, the variance of 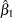 for the normal regression and logistic regression models is inversely related to the variance of X1 after adjusting for other covariates. That is,
for the normal regression and logistic regression models is inversely related to the variance of X1 after adjusting for other covariates. That is,
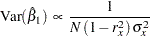 |
where 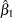 is the estimate of the parameter
is the estimate of the parameter 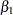 in the model and
in the model and 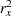 is the R square from the regression of
is the R square from the regression of 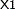 on other covariates—that is, the proportion of the variance
on other covariates—that is, the proportion of the variance 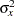 explained by these covariates.
explained by these covariates.
Similarly, for a proportional hazards regression model,
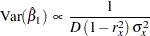 |
Thus, with the derived maximum information, the required sample size or number of events can also be computed for the testing of a parameter in a regression model with covariates.
Test for a Parameter in the Regression Model
The MODEL=REG option in the SAMPLESIZE statement derives the sample size required for a 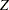 test of a normal regression. For a normal linear regression model, the response variable is normally distributed with the mean equal to a linear function of the explanatory variables and the constant variance
test of a normal regression. For a normal linear regression model, the response variable is normally distributed with the mean equal to a linear function of the explanatory variables and the constant variance 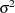 .
.
The normal linear model is
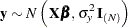 |
where  is the vector of the
is the vector of the 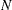 observed responses,
observed responses, 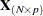 is the design matrix for these
is the design matrix for these 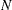 observations,
observations,  is the parameter vector, and
is the parameter vector, and 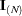 is the
is the 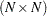 identity matrix.
identity matrix.
The least squares estimate is
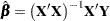 |
and is normally distributed with mean 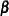 and variance
and variance
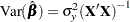 |
For a model with only one covariate X1,
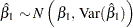 |
where the variance
 |
Thus, with the derived maximum information 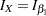 , the required sample size is given by
, the required sample size is given by
 |
For a normal linear model with more than one covariate, the variance of a single parameter 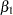 is
is
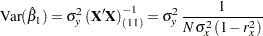 |
where  is the diagonal element of the
is the diagonal element of the 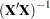 matrix corresponding to the parameter
matrix corresponding to the parameter 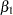 ,
, 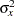 is the variance of the variable X1, and
is the variance of the variable X1, and 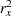 is the proportion of variance of X1 explained by other covariates. The value
is the proportion of variance of X1 explained by other covariates. The value  represents the variance of X1 after adjusting for all other covariates.
represents the variance of X1 after adjusting for all other covariates.
Thus, with the derived maximum information 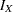 , the required sample size is
, the required sample size is
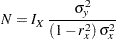 |
In the SEQDESIGN procedure, you can specify the MODEL=REG( VARIANCE=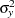 XVARIANCE=
XVARIANCE=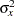 XRSQUARE=
XRSQUARE=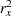 ) option in the SAMPLESIZE statement to compute the required total sample size and individual sample size at each stage. A SAS procedure such as PROC REG can be used to compute the parameter estimate and its standard error at each stage.
) option in the SAMPLESIZE statement to compute the required total sample size and individual sample size at each stage. A SAS procedure such as PROC REG can be used to compute the parameter estimate and its standard error at each stage.
Test for a Parameter in the Logistic Regression Model
The MODEL=LOGISTIC option in the SAMPLESIZE statement derives the sample size required for a 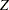 test of a logistic regression parameter. The linear logistic model has the form
test of a logistic regression parameter. The linear logistic model has the form
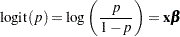 |
where 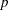 is the response probability to be modeled and
is the response probability to be modeled and 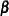 is a vector of parameters.
is a vector of parameters.
Following the derivation in the section Test for a Parameter in the Regression Model, the required sample size for testing a parameter in 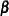 is given by
is given by
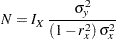 |
With the variance of the logit response, 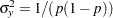 ,
,
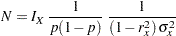 |
where 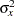 is the variance of X and
is the variance of X and 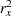 is the proportion of variance explained by other covariates.
is the proportion of variance explained by other covariates.
In the SEQDESIGN procedure, you can specify the MODEL=LOGISTIC( PROP=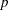 XVARIANCE=
XVARIANCE=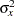 XRSQUARE=
XRSQUARE=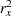 ) option in the SAMPLESIZE statement to compute the required total sample size and individual sample size at each stage.
) option in the SAMPLESIZE statement to compute the required total sample size and individual sample size at each stage.
A SAS procedure such as PROC LOGISTIC can be used to compute the parameter estimate and its standard error at each stage.
Test for a Parameter in the Proportional Hazards Regression Model
The MODEL=PHREG option in the SAMPLESIZE statement derives the number of events required for a 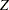 test of a proportional hazards regression parameter. For analyses of survival data, Cox’s semiparametric model is often used to examine the effect of explanatory variables on hazard rates. The survival time of each observation in the population is assumed to follow its own hazard function,
test of a proportional hazards regression parameter. For analyses of survival data, Cox’s semiparametric model is often used to examine the effect of explanatory variables on hazard rates. The survival time of each observation in the population is assumed to follow its own hazard function, 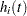 , expressed as
, expressed as
 |
where 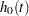 is an arbitrary and unspecified baseline hazard function,
is an arbitrary and unspecified baseline hazard function, 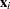 is the vector of explanatory variables for the
is the vector of explanatory variables for the 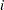 th individual, and
th individual, and 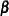 is the vector of regression parameters associated with the explanatory variables.
is the vector of regression parameters associated with the explanatory variables.
Hsieh and Lavori (2000, p. 553) show that the required number of events for testing a parameter in 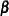 ,
, 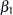 , associated with the variable X1 is given by
, associated with the variable X1 is given by
 |
where 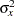 is the variance of X1 and
is the variance of X1 and 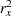 is the proportion of variance of X1 explained by other covariates.
is the proportion of variance of X1 explained by other covariates.
In the SEQDESIGN procedure, you can specify the MODEL=PHREG( XVARIANCE=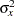 XRSQUARE=
XRSQUARE=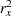 ) option in the SAMPLESIZE statement to compute the required number of events and individual number of events at each stage.
) option in the SAMPLESIZE statement to compute the required number of events and individual number of events at each stage.
A SAS procedure such as PROC PHREG can be used to compute the parameter estimate and its standard error at each stage.
Note that for a two-sample test, X1 is an indicator variable and is the only covariate in the model. Thus, if the two sample sizes are equal, then the variance 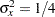 and the required number of events for testing the parameter
and the required number of events for testing the parameter 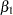 is given by
is given by
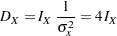 |
See the section Input Number of Events for Fixed-Sample Design for a detailed description of the sample size computation that uses hazard rates, accrual rate, and accrual time.
Copyright © SAS Institute, Inc. All Rights Reserved.