| The SEQDESIGN Procedure |
| Aspects of Group Sequential Designs |
This section summarizes various aspects of group sequential designs that are encountered in applications of the SEQDESIGN procedure. Features are illustrated through two-sided designs with 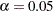 and
and 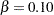 . The null hypothesis
. The null hypothesis 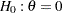 and an alternative reference
and an alternative reference  are used for the designs with early stopping only to reject the null hypothesis.
are used for the designs with early stopping only to reject the null hypothesis.
Canonical Joint Distribution
The SEQDESIGN procedure assumes that with a total number of stages 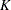 , the sequence of the standardized test statistics
, the sequence of the standardized test statistics  has the canonical joint distribution with information levels
has the canonical joint distribution with information levels 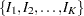 for the parameter
for the parameter 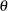 (Jennison and Turnbull 2000, p. 49):
(Jennison and Turnbull 2000, p. 49):
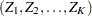 is multivariate normal
is multivariate normal 
 ,
, 
Normality Assumption
The SEQDESIGN procedure derives the boundary values by assuming that the sequence of the standardized test statistics  has the canonical joint distribution with information levels
has the canonical joint distribution with information levels 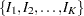 for the parameter
for the parameter 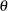 . If the test statistic
. If the test statistic 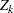 does not have a normal distribution, it is assumed that the test statistic is computed from a large sample, so that the resulting statistic has an approximately normal distribution.
does not have a normal distribution, it is assumed that the test statistic is computed from a large sample, so that the resulting statistic has an approximately normal distribution.
Number of Stages
For group sequential trials with fixed significance level  , power
, power 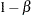 , and alternative reference, if the number of stages is increased, the required maximum information is also increased, but the average sample number under the alternative hypothesis is likely to decrease.
, and alternative reference, if the number of stages is increased, the required maximum information is also increased, but the average sample number under the alternative hypothesis is likely to decrease.
For example, for two-sided designs with early stopping only to reject the null hypothesis 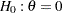 ,
, 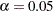 , and
, and 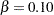 at the alternative reference
at the alternative reference  , the O’Brien-Fleming method increases the maximum information from
, the O’Brien-Fleming method increases the maximum information from  for a fixed-sample design to
for a fixed-sample design to  for a two-stage design,
for a two-stage design,  for a five-stage design, and then
for a five-stage design, and then 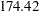 for a ten-stage design. In the mean time, the average sample number (as a percentage of fixed-sample) under the alternative hypothesis decreases from
for a ten-stage design. In the mean time, the average sample number (as a percentage of fixed-sample) under the alternative hypothesis decreases from 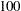 for a fixed-sample design to
for a fixed-sample design to 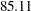 for a two-stage design,
for a two-stage design,  for a five-stage design, and then
for a five-stage design, and then 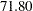 for a ten-stage design. The reduction in average sample number decreases as the number of stages increases. Thus there seems to be little to gain from choosing a design with more than five stages (Pocock 1982, p. 155).
for a ten-stage design. The reduction in average sample number decreases as the number of stages increases. Thus there seems to be little to gain from choosing a design with more than five stages (Pocock 1982, p. 155).
Alternative Reference
The alternative reference 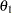 is the hypothetical reference under the alternative hypothesis at which the power is computed. It is a treatment value that the investigators would hope to detect with high probability (Jennison and Turnbull 2000, p. 21).
is the hypothetical reference under the alternative hypothesis at which the power is computed. It is a treatment value that the investigators would hope to detect with high probability (Jennison and Turnbull 2000, p. 21).
For a group sequential design with specified parameters such as  and
and  errors, the drift parameter
errors, the drift parameter  is always derived in the SEQDESIGN procedure. Thus, with a smaller alternative reference
is always derived in the SEQDESIGN procedure. Thus, with a smaller alternative reference 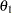 , a larger maximum information level
, a larger maximum information level 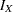 is needed. That is, in order to detect a smaller difference with the same high power, a larger sample size is required.
is needed. That is, in order to detect a smaller difference with the same high power, a larger sample size is required.
Maximum Information
In a clinical trial, the amount of information about an unknown parameter available from the data can be measured by the Fisher information, the variance of the score statistic. The maximum information is the information level needed at the final stage of the group sequential trial if the trial does not stop at an interim stage. For a group sequential design, the maximum information can be derived with the specified alternative reference.
The maximum information is proportional to the sample size or number of events required for the design. Thus, it can also be used to compare different designs. Generally, a design with a larger probability to stop the trial early tends to have a larger maximum information. For example, for two-sided four-stage designs with early stopping only to reject 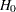 ,
, 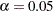 , and
, and 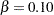 at the alternative reference
at the alternative reference  , the Pocock method has a maximum information of
, the Pocock method has a maximum information of  and the O’Brien-Fleming method has a maximum information of
and the O’Brien-Fleming method has a maximum information of  , indicating a much larger information level required for the Pocock method.
, indicating a much larger information level required for the Pocock method.
Drift Parameter
The drift parameter  is derived for each design in the SEQDESIGN procedure, where
is derived for each design in the SEQDESIGN procedure, where 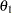 is the alternative reference. It is proportional to the square root of maximum information required for the design and can be used to compare maximum information for different designs with the same alternative reference. For example, for two-sided four-stage designs with early stopping only to reject
is the alternative reference. It is proportional to the square root of maximum information required for the design and can be used to compare maximum information for different designs with the same alternative reference. For example, for two-sided four-stage designs with early stopping only to reject 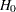 ,
, 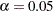 , and
, and 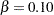 , the Pocock method has a drift parameter
, the Pocock method has a drift parameter  and the O’Brien-Fleming method has a drift parameter
and the O’Brien-Fleming method has a drift parameter  , indicating that a larger maximum information level is required for the Pocock method than for the O’Brien-Fleming method.
, indicating that a larger maximum information level is required for the Pocock method than for the O’Brien-Fleming method.
Average Sample Number
The average sample number is the expected sample size (for nonsurvival data) or expected number of events (for survival data) of the design under a specific hypothetical reference. The percent average sample numbers with respect to the corresponding fixed-sample design are displayed in the SEQDESIGN procedure.
The design that requires a larger maximum information level tends to have a smaller average sample number under the alternative hypothesis. For example, for two-sided four-stage designs with early stopping only to reject 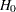 ,
, 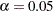 , and
, and 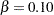 at the alternative reference
at the alternative reference  , the Pocock design has a maximum information of
, the Pocock design has a maximum information of  and an average sample number (in percentage of fixed-sample design) of
and an average sample number (in percentage of fixed-sample design) of 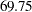 under the alternative hypothesis, and the O’Brien-Fleming design has a maximum information of
under the alternative hypothesis, and the O’Brien-Fleming design has a maximum information of  and an average sample number of
and an average sample number of 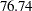 .
.
Sample Size
The maximum information for the sequential design expressed as a percentage of its corresponding fixed-sample information is derived in the SEQDESIGN procedure. The sample size or number of events needed for a group sequential trial is computed by multiplying the sample size or number of events for the corresponding fixed-sample design by the derived percentage.
If the sample size or number of events for the fixed-sample design is available, you can use the MODEL=INPUTNOBS or MODEL=INPUTNEVENTS option in the SAMPLESIZE statement to derive the sample size or number of events needed at each stage. Otherwise, with the specified or derived maximum information, you can use the MODEL= option in the SAMPLESIZE statement to specify a hypothesis test and then to derive the sample size or number of events needed at each stage. See the section Sample Size Computation for the sample size computation for commonly used tests.
Copyright © SAS Institute, Inc. All Rights Reserved.