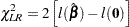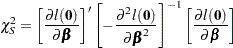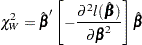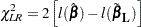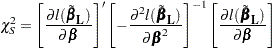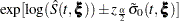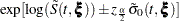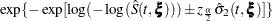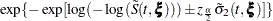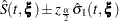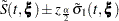| The PHREG Procedure |
| Specifics for Classical Analysis |
Proportional Rates/Means Models for Recurrent Events
Let 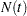 be the number of events experienced by a subject over the time interval
be the number of events experienced by a subject over the time interval 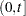 . Let
. Let 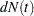 be the increment of the counting process
be the increment of the counting process 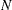 over
over 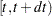 . The rate function is given by
. The rate function is given by
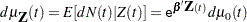 |
where 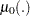 is an unknown continuous function. If the
is an unknown continuous function. If the 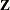 are time independent, the rate model is reduced to the mean model
are time independent, the rate model is reduced to the mean model
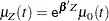 |
The partial likelihood for  independent triplets
independent triplets 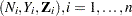 , of counting, at-risk, and covariate processes is the same as that of the multiplicative hazards model. However, a robust sandwich estimate is used for the covariance matrix of the parameter estimator instead of the model-based estimate.
, of counting, at-risk, and covariate processes is the same as that of the multiplicative hazards model. However, a robust sandwich estimate is used for the covariance matrix of the parameter estimator instead of the model-based estimate.
Let 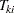 be the
be the 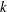 th event time of the
th event time of the  th subject. Let
th subject. Let 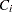 be the censoring time of the
be the censoring time of the  th subject. The at-risk indicator and the failure indicator are, respectively,
th subject. The at-risk indicator and the failure indicator are, respectively,
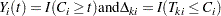 |
Denote
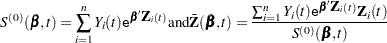 |
Let 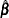 be the maximum likelihood estimate of
be the maximum likelihood estimate of 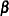 , and let
, and let 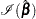 be the observed information matrix. The robust sandwich covariance matrix estimate is given by
be the observed information matrix. The robust sandwich covariance matrix estimate is given by
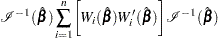 |
where
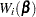 |
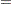 |
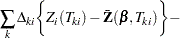 |
|||
 |
 |
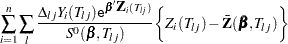 |
For a given realization of the covariates 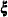 , the Nelson estimator is used to predict the mean function
, the Nelson estimator is used to predict the mean function
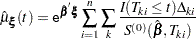 |
with standard error estimate given by
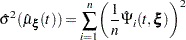 |
where
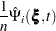 |
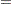 |
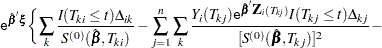 |
|||
 |
 |
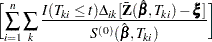 |
|||
 |
 |
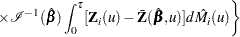 |
Since the cumulative mean function is always nonnegative, the log transform is used to compute confidence intervals. The 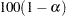 % pointwise confidence limits for
% pointwise confidence limits for 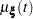 are
are
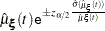 |
where  is the upper
is the upper 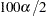 percentage point of the standard normal distribution.
percentage point of the standard normal distribution.
Newton-Raphson Method
Let 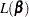 be one of the likelihood functions described in the previous subsections. Let
be one of the likelihood functions described in the previous subsections. Let 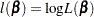 . Finding
. Finding 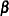 such that
such that 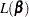 is maximized is equivalent to finding the solution
is maximized is equivalent to finding the solution 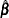 to the likelihood equations
to the likelihood equations
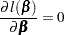 |
With 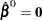 as the initial solution, the iterative scheme is expressed as
as the initial solution, the iterative scheme is expressed as
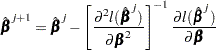 |
The term after the minus sign is the Newton-Raphson step. If the likelihood function evaluated at 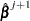 is less than that evaluated at
is less than that evaluated at  , then
, then 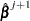 is recomputed using half the step size. The iterative scheme continues until convergence is obtained—that is, until
is recomputed using half the step size. The iterative scheme continues until convergence is obtained—that is, until 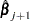 is sufficiently close to
is sufficiently close to 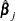 . Then the maximum likelihood estimate of
. Then the maximum likelihood estimate of 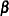 is
is 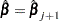 .
.
The model-based variance estimate of 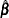 is obtained by inverting the information matrix
is obtained by inverting the information matrix 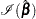
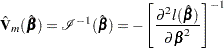 |
Firth’s Modification for Maximum Likelihood Estimation
In fitting a Cox model, the phenomenon of monotone likelihood is observed if the likelihood converges to a finite value while at least one parameter diverges (Heinze and Schemper; 2001).
Let 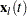 denote the vector explanatory variables for the
denote the vector explanatory variables for the 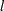 th individual at time
th individual at time  . Let
. Let 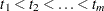 denote the
denote the 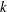 distinct, ordered event times. Let
distinct, ordered event times. Let 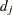 denote the multiplicity of failures at
denote the multiplicity of failures at 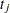 ; that is,
; that is, 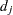 is the size of the set
is the size of the set 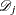 of individuals that fail at
of individuals that fail at 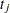 . Let
. Let 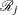 denote the risk set just before
denote the risk set just before 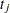 . Let
. Let 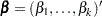 be the vector of regression parameters. The Breslow log partial likelihood is given by
be the vector of regression parameters. The Breslow log partial likelihood is given by
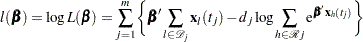 |
Denote
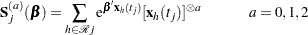 |
Then the score function is given by
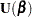 |
 |
 |
|||
 |
 |
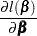 |
|||
 |
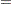 |
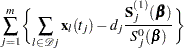 |
and the Fisher information matrix is given by
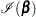 |
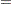 |
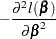 |
|||
 |
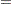 |
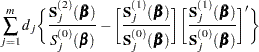 |
Heinze (1999); Heinze and Schemper (2001) applied the idea of Firth (1993) by maximizing the penalized partial likelihood
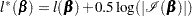 |
The score function 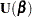 is replaced by the modified score function by
is replaced by the modified score function by 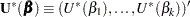 , where
, where
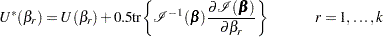 |
The Firth estimate is obtained iteratively as
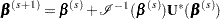 |
The covariance matrix 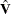 is computed as
is computed as 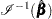 , where
, where 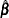 is the maximum penalized partial likelihood estimate.
is the maximum penalized partial likelihood estimate.
Explicit formulae for 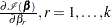
Denote
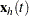 |
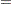 |
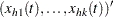 |
|||
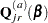 |
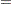 |
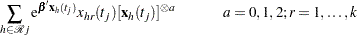 |
Then
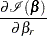 |
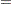 |
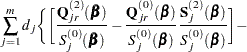 |
|||
 |
 |
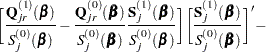 |
|||
 |
 |
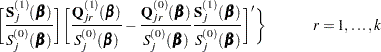 |
Robust Sandwich Variance Estimate
For the  th subject,
th subject, 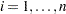 , let
, let 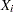 ,
, 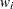 , and
, and 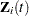 be the observed time, weight, and the covariate vector at time
be the observed time, weight, and the covariate vector at time  , respectively. Let
, respectively. Let 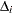 be the event indicator and let
be the event indicator and let 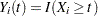 . Let
. Let
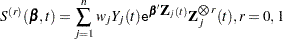 |
Let 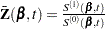 . The score residual for the
. The score residual for the  th subject is
th subject is
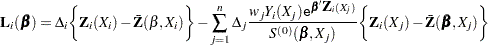 |
For TIES=EFRON, the computation of the score residuals is modified to comply with the Efron partial likelihood. See the section Residuals for more information.
The robust sandwich variance estimate of 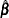 derived by Binder (1992), who incorporated weights into the analysis, is
derived by Binder (1992), who incorporated weights into the analysis, is
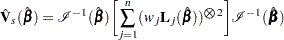 |
where 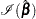 is the observed information matrix, and
is the observed information matrix, and 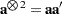 . Note that when
. Note that when 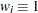 ,
,
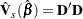 |
where 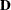 is the matrix of DFBETA residuals. This robust variance estimate was proposed by Lin and Wei (1989) and Reid and Crèpeau (1985).
is the matrix of DFBETA residuals. This robust variance estimate was proposed by Lin and Wei (1989) and Reid and Crèpeau (1985).
Testing the Global Null Hypothesis
The following statistics can be used to test the global null hypothesis 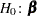 =
=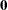 . Under mild assumptions, each statistic has an asymptotic chi-square distribution with
. Under mild assumptions, each statistic has an asymptotic chi-square distribution with 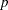 degrees of freedom given the null hypothesis. The value
degrees of freedom given the null hypothesis. The value 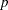 is the dimension of
is the dimension of 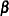 . For clustered data, the likelihood ratio test, the score test, and the Wald test assume independence of observations within a cluster, while the robust Wald test and the robust score test do not need such an assumption.
. For clustered data, the likelihood ratio test, the score test, and the Wald test assume independence of observations within a cluster, while the robust Wald test and the robust score test do not need such an assumption.
Robust Score Test
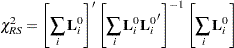 |
where 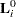 is the score residual of the
is the score residual of the  th subject at
th subject at 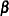 =
=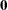 ; that is,
; that is, 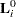 =
= , where the score process
, where the score process 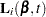 is defined in the section Residuals.
is defined in the section Residuals.
Robust Wald’s Test
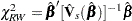 |
where 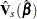 is the sandwich variance estimate (see the section Robust Sandwich Variance Estimate for details).
is the sandwich variance estimate (see the section Robust Sandwich Variance Estimate for details).
Type 3 Tests
The following statistics can be used to test the null hypothesis 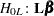 =
=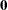 , where
, where  is a matrix of known coefficients. Under mild assumptions, each of the following statistics has an asymptotic chi-square distribution with
is a matrix of known coefficients. Under mild assumptions, each of the following statistics has an asymptotic chi-square distribution with 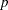 degrees of freedom, where
degrees of freedom, where 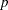 is the rank of
is the rank of  . Let
. Let 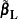 be the maximum likelihood of
be the maximum likelihood of 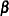 under the null hypothesis
under the null hypothesis 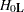 ; that is,
; that is,
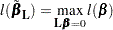 |
Wald’s Statistic
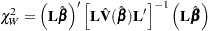 |
where 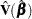 is the estimated covariance matrix, which can be the model-based covariance matrix
is the estimated covariance matrix, which can be the model-based covariance matrix 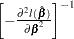 or the sandwich covariance matrix
or the sandwich covariance matrix 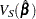 (see the section Robust Sandwich Variance Estimate for details).
(see the section Robust Sandwich Variance Estimate for details).
Confidence Limits for a Hazard Ratio
Let 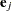 be the
be the 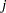 th unit vector—that is, the
th unit vector—that is, the 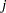 th entry of the vector is 1 and all other entries are 0. The hazard ratio for the explanatory variable with regression coefficient
th entry of the vector is 1 and all other entries are 0. The hazard ratio for the explanatory variable with regression coefficient 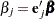 is defined as
is defined as 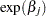 . In general, a log-hazard ratio can be written as
. In general, a log-hazard ratio can be written as 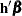 , a linear combination of the regression coefficients, and the hazard ratio
, a linear combination of the regression coefficients, and the hazard ratio 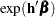 is obtained by replacing
is obtained by replacing 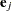 with
with 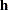 .
.
Point Estimate
The hazard ratio 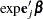 is estimated by
is estimated by 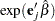 , where
, where 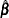 is the maximum likelihood estimate of the
is the maximum likelihood estimate of the 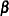 .
.
Wald’s Confidence Limits
The 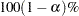 confidence limits for the hazard ratio are calculated as
confidence limits for the hazard ratio are calculated as
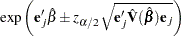 |
where 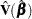 is estimated covariance matrix, and
is estimated covariance matrix, and  is the
is the 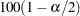 percentile point of the standard normal distribution.
percentile point of the standard normal distribution.
Profile-Likelihood Confidence Limits
The construction of the profile-likelihood-based confidence interval is derived from the asymptotic 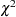 distribution of the generalized likelihood ratio test of Venzon and Moolgavkar (1988). Suppose that the parameter vector is
distribution of the generalized likelihood ratio test of Venzon and Moolgavkar (1988). Suppose that the parameter vector is 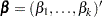 and you want to compute a confidence interval for
and you want to compute a confidence interval for 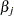 . The profile-likelihood function for
. The profile-likelihood function for 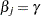 is defined as
is defined as
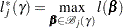 |
where 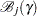 is the set of all
is the set of all 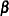 with the
with the 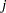 th element fixed at
th element fixed at 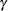 , and
, and 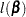 is the log-likelihood function for
is the log-likelihood function for 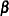 . If
. If 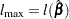 is the log likelihood evaluated at the maximum likelihood estimate
is the log likelihood evaluated at the maximum likelihood estimate 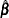 , then
, then  has a limiting chi-square distribution with one degree of freedom if
has a limiting chi-square distribution with one degree of freedom if 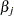 is the true parameter value. Let
is the true parameter value. Let 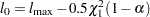 , where
, where 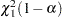 is the
is the 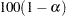 percentile of the chi-square distribution with one degree of freedom. A
percentile of the chi-square distribution with one degree of freedom. A 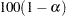 % confidence interval for
% confidence interval for 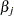 is
is
 |
The endpoints of the confidence interval are found by solving numerically for values of 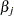 that satisfy equality in the preceding relation. To obtain an iterative algorithm for computing the confidence limits, the log-likelihood function in a neighborhood of
that satisfy equality in the preceding relation. To obtain an iterative algorithm for computing the confidence limits, the log-likelihood function in a neighborhood of 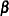 is approximated by the quadratic function
is approximated by the quadratic function
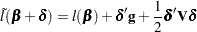 |
where 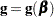 is the gradient vector and
is the gradient vector and 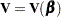 is the Hessian matrix. The increment
is the Hessian matrix. The increment 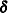 for the next iteration is obtained by solving the likelihood equations
for the next iteration is obtained by solving the likelihood equations
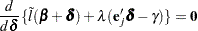 |
where 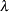 is the Lagrange multiplier,
is the Lagrange multiplier, 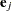 is the
is the 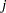 th unit vector, and
th unit vector, and 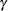 is an unknown constant. The solution is
is an unknown constant. The solution is
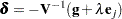 |
By substituting this 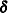 into the equation
into the equation 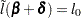 , you can estimate
, you can estimate 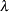 as
as
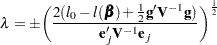 |
The upper confidence limit for 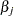 is computed by starting at the maximum likelihood estimate of
is computed by starting at the maximum likelihood estimate of 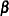 and iterating with positive values of
and iterating with positive values of 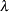 until convergence is attained. The process is repeated for the lower confidence limit, using negative values of
until convergence is attained. The process is repeated for the lower confidence limit, using negative values of 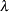 .
.
Convergence is controlled by value  specified with the PLCONV= option in the MODEL statement (the default value of
specified with the PLCONV= option in the MODEL statement (the default value of  is 1E
is 1E 4). Convergence is declared on the current iteration if the following two conditions are satisfied:
4). Convergence is declared on the current iteration if the following two conditions are satisfied:
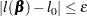 |
and
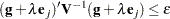 |
The profile-likelihood confidence limits for the hazard ratio 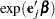 are obtained by exponentiating these confidence limits.
are obtained by exponentiating these confidence limits.
Using the TEST Statement to Test Linear Hypotheses
Linear hypotheses for 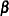 are expressed in matrix form as
are expressed in matrix form as
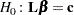 |
where L is a matrix of coefficients for the linear hypotheses, and c is a vector of constants. The Wald chi-square statistic for testing 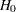 is computed as
is computed as
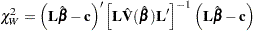 |
where 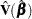 is the estimated covariance matrix. Under
is the estimated covariance matrix. Under 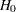 ,
, 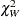 has an asymptotic chi-square distribution with r degrees of freedom, where r is the rank of
has an asymptotic chi-square distribution with r degrees of freedom, where r is the rank of  .
.
Optimal Weights for the AVERAGE option in the TEST Statement
Let 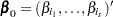 , where
, where 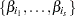 is a subset of
is a subset of  regression coefficients. For any vector
regression coefficients. For any vector 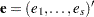 of length
of length  ,
,
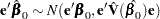 |
To find  such that
such that 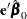 has the minimum variance, it is necessary to minimize
has the minimum variance, it is necessary to minimize 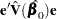 subject to
subject to 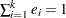 . Let
. Let 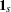 be a vector of 1’s of length
be a vector of 1’s of length  . The expression to be minimized is
. The expression to be minimized is
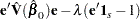 |
where 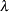 is the Lagrange multipler. Differentiating with respect to
is the Lagrange multipler. Differentiating with respect to  and
and 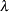 , respectively, yields
, respectively, yields
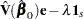 |
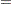 |
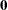 |
|||
 |
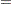 |
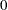 |
Solving these equations gives
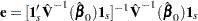 |
This provides a one degree-of-freedom test for testing the null hypothesis  with normal test statistic
with normal test statistic
 |
This test is more sensitive than the multivariate test specified by the TEST statement
Multivariate: test X1, ..., Xs;
where X , ..., X
, ..., X are the variables with regression coefficients
are the variables with regression coefficients 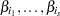 , respectively.
, respectively.
Analysis of Multivariate Failure Time Data
Multivariate failure time data arise when each study subject can potentially experience several events (for instance, multiple infections after surgery) or when there exists some natural or artificial clustering of subjects (for instance, a litter of mice) that induces dependence among the failure times of the same cluster. Data in the former situation are referred to as multiple events data, and data in the latter situation are referred to as clustered data. The multiple events data can be further classified into ordered and unordered data. For ordered data, there is a natural ordering of the multiple failures within a subject, which includes recurrent events data as a special case. For unordered data, the multiple event times result from several concurrent failure processes.
Multiple events data can be analyzed by the Wei, Lin, and Weissfeld (1989), or WLW, method based on the marginal Cox models. For the special case of recurrent events data, you can fit the intensity model (Andersen and Gill; 1982), the proportional rates/means model (Pepe and Cai 1993; Lawless and Nadeau 1995; Lin et al. 2000), or the stratified models for total time and gap time proposed by Prentice, Williams, and Peterson (1981), or PWP. For clustered data, you can carry out the analysis of Lee, Wei, and Amato (1992) based on the marginal Cox model. To use PROC PHREG to perform these analyses correctly and effectively, you have to array your data in a specific way to produce the correct risk sets.
All examples described in this section can be found in the program phrmult.sas in the SAS/STAT sample library. Furthermore, the "Examples" section in this chapter contains two examples to illustrate the methods of analyzing recurrent events data and clustered data.
Marginal Cox Models for Multiple Events Data
Suppose there are  subjects and each subject can experience up to
subjects and each subject can experience up to 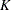 potential events. Let
potential events. Let 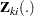 be the covariate process associated with the
be the covariate process associated with the 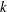 th event for the
th event for the  th subject. The marginal Cox models are given by
th subject. The marginal Cox models are given by
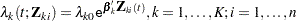 |
where 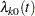 is the (event-specific) baseline hazard function for the
is the (event-specific) baseline hazard function for the 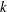 th event and
th event and 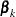 is the (event-specific) column vector of regression coefficients for the
is the (event-specific) column vector of regression coefficients for the 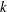 th event. WLW estimates
th event. WLW estimates 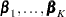 by the maximum partial likelihood estimates
by the maximum partial likelihood estimates 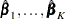 , respectively, and uses a robust sandwich covariance matrix estimate for
, respectively, and uses a robust sandwich covariance matrix estimate for 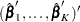 to account for the dependence of the multiple failure times.
to account for the dependence of the multiple failure times.
By using a properly prepared input data set, you can estimate the regression parameters for all the marginal Cox models and compute the robust sandwich covariance estimates in one PROC PHREG invocation. For convenience of discussion, suppose each subject can potentially experience 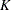 =3 events and there are two explanatory variables Z1 and Z2. The event-specific parameters to be estimated are
=3 events and there are two explanatory variables Z1 and Z2. The event-specific parameters to be estimated are 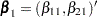 for the first marginal model,
for the first marginal model, 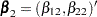 for the second marginal model, and
for the second marginal model, and 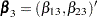 for the third marginal model. Inference of these parameters is based on the robust sandwich covariance matrix estimate of the parameter estimators. It is necessary that each row of the input data set represent the data for a potential event of a subject. The input data set should contain the following:
for the third marginal model. Inference of these parameters is based on the robust sandwich covariance matrix estimate of the parameter estimators. It is necessary that each row of the input data set represent the data for a potential event of a subject. The input data set should contain the following:
an ID variable for identifying the subject so that all observations of the same subject have the same ID value
an Enum variable to index the multiple events. For example, Enum=1 for the first event, Enum=2 for the second event, and so on.
a Time variable to represent the observed time from some time origin for the event. For recurrence events data, it is the time from the study entry to each recurrence.
a Status variable to indicate whether the Time value is a censored or uncensored time. For example, Status=1 indicates an uncensored time and Status=0 indicates a censored time.
independent variables (Z1 and Z2)
The WLW analysis can be carried out by specifying the following:
proc phreg covs(aggregate); model Time*Status(0)=Z11 Z12 Z13 Z21 Z22 Z23; strata Enum; id ID; Z11= Z1 * (Enum=1); Z12= Z1 * (Enum=2); Z13= Z1 * (Enum=3); Z21= Z2 * (Enum=1); Z22= Z2 * (Enum=2); Z23= Z2 * (Enum=3); run;
The variable Enum is specified in the STRATA statement so that there is one marginal Cox model for each distinct value of Enum. The variables Z11, Z12, Z13, Z21, Z22, and Z23 in the MODEL statement are event-specific variables derived from the independent variables Z1 and Z2 by the given programming statements. In particular, the variables Z11, Z12, and Z13 are event-specific variables for the explanatory variable Z1; the variables Z21, Z22, and Z23 are event-specific variables for the explanatory variable Z2. For 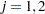 , and
, and 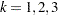 , variable Zjk contains the same values as the explanatory variable Zj for the rows that correspond to
, variable Zjk contains the same values as the explanatory variable Zj for the rows that correspond to 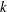 th marginal model and the value 0 for all other rows; as such,
th marginal model and the value 0 for all other rows; as such, 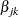 is the regression coefficient for Zjk. You can avoid using the programming statements in PROC PHREG if you create these event-specific variables in the input data set by using the same programming statements in a DATA step.
is the regression coefficient for Zjk. You can avoid using the programming statements in PROC PHREG if you create these event-specific variables in the input data set by using the same programming statements in a DATA step.
The option COVS(AGGREGATE) is specified in the PROC statement to obtain the robust sandwich estimate of the covariance matrix, and the score residuals used in computing the middle part of the sandwich estimate are aggregated over identical ID values. You can also include TEST statements in the PROC PHREG code to test various linear hypotheses of the regression parameters based on the robust sandwich covariance matrix estimate.
Consider the AIDS study data in Wei, Lin, and Weissfeld (1989) from a randomized clinical trial to assess the antiretroviral capacity of ribavirin over time in AIDS patients. Blood samples were collected at weeks 4, 8, and 12 from each patient in three treatment groups (placebo, low dose of ribavirin, and high dose). For each serum sample, the failure time is the number of days before virus positivity was detected. If the sample was contaminated or it took a longer period of time than was achievable in the laboratory, the sample was censored. For example:
Patient #1 in the placebo group has uncensored times 9, 6, and 7 days (that is, it took 9 days to detect viral positivity in the first blood sample, 6 days for the second blood sample, and 7 days for the third blood sample).
Patient #14 in the low-dose group of ribavirin has uncensored times of 16 and 17 days for the first and second sample, respectively, and a censored time of 21 days for the third blood sample.
Patient #28 in the high-dose group has an uncensored time of 21 days for the first sample, no measurement for the second blood sample, and a censored time of 25 days for the third sample.
For a full-rank parameterization, two design variables are sufficient to represent three treatment groups. Based on the reference coding with placebo as the reference, the values of the two dummy explanatory variables Z1 and Z2 representing the treatments are as follows:
Treatment Group |
Z1 |
Z2 |
Placebo |
0 |
0 |
Low dose ribavirin |
1 |
0 |
High dose ribavirin |
0 |
1 |
The bulk of the task in using PROC PHREG to perform the WLW analysis lies in the preparation of the input data set. As discussed earlier, the input data set should contain the ID, Enum, Time, and Status variables, and event-specific independent variables Z11, Z12, Z13, Z21, Z22, and Z23. Data for the three patients described earlier are arrayed as follows:
ID |
Time |
Status |
Enum |
Z1 |
Z2 |
1 |
9 |
1 |
1 |
0 |
0 |
1 |
6 |
1 |
2 |
0 |
0 |
1 |
7 |
1 |
3 |
0 |
0 |
14 |
16 |
1 |
1 |
1 |
0 |
14 |
17 |
1 |
2 |
1 |
0 |
14 |
21 |
0 |
3 |
1 |
0 |
28 |
21 |
1 |
1 |
0 |
1 |
28 |
25 |
0 |
3 |
0 |
1 |
The first three rows are data for Patient #1 with event times at 9, 6, and 7 days, one row for each event. The next three rows are data for Patient #14, who has an uncensored time of 16 days for the first serum sample, an uncensored time of 17 days for the second sample, and a censored time of 21 days for the third sample. The last two rows are data for Patient #28 of the high-dose group (Z1=0 and Z2=1). Since the patient did not have a second serum sample, there are only two rows of data.
To perform the WLW analysis, you specify the following statements:
proc phreg covs(aggregate); model Time*Status(0)=Z11 Z12 Z13 Z21 Z22 Z23; strata Enum; id ID; Z11= Z1 * (Enum=1); Z12= Z1 * (Enum=2); Z13= Z1 * (Enum=3); Z21= Z2 * (Enum=1); Z22= Z2 * (Enum=2); Z23= Z2 * (Enum=3); EqualLowDose: test Z11=Z12, Z12=Z23; AverageLow: test Z11,Z12,Z13 / e average; run;
Two linear hypotheses are tested using the TEST statements. The specification
EqualLowDose: test Z11=Z12, Z12=Z13;
tests the null hypothesis 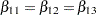 of identical low-dose effects across three marginal models. The specification
of identical low-dose effects across three marginal models. The specification
AverageLow: test Z11,Z12,Z13 / e average;
tests the null hypothesis of no low-dose effects (that is, 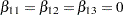 ). The AVERAGE option computes the optimal weights for estimating the average low-dose effect
). The AVERAGE option computes the optimal weights for estimating the average low-dose effect 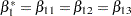 and performs a 1 DF test for testing the null hypothesis that
and performs a 1 DF test for testing the null hypothesis that 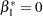 . The E option displays the coefficients for the linear hypotheses, including the optimal weights.
. The E option displays the coefficients for the linear hypotheses, including the optimal weights.
Marginal Cox Models for Clustered Data
Suppose there are  clusters with
clusters with 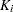 members in the
members in the  th cluster,
th cluster, 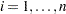 . Let
. Let 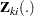 be the covariate process associated with the
be the covariate process associated with the 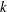 th member of the
th member of the  th cluster. The marginal Cox model is given by
th cluster. The marginal Cox model is given by
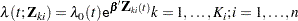 |
where 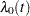 is an arbitrary baseline hazard function and
is an arbitrary baseline hazard function and 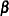 is the vector of regression coefficients. Lee, Wei, and Amato (1992) estimate
is the vector of regression coefficients. Lee, Wei, and Amato (1992) estimate 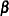 by the maximum partial likelihood estimate
by the maximum partial likelihood estimate 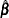 under the independent working assumption, and use a robust sandwich covariance estimate to account for the intracluster dependence.
under the independent working assumption, and use a robust sandwich covariance estimate to account for the intracluster dependence.
To use PROC PHREG to analyze the clustered data, each member of a cluster is represented by an observation in the input data set. The input data set to PROC PHREG should contain the following:
an ID variable to identify the cluster so that members of the same cluster have the same ID value
a Time variable to represent the observed survival time of a member of a cluster
a Status variable to indicate whether the Time value is an uncensored or censored time. For example, Status=1 indicates an uncensored time and Status=0 indicates a censored time.
the explanatory variables thought to be related to the failure time
Consider a tumor study in which one of three female rats of the same litter was randomly subjected to a drug treatment. The failure time is the time from randomization to the detection of tumor. If a rat died before the tumor was detected, the failure time was censored. For example:
In litter #1, the drug-treated rat has an uncensored time of 101 days, one untreated rat has a censored time of 49 days, and the other untreated rat has a failure time of 104 days.
In litter #3, the drug-treated rat has a censored time of 104 days, one untreated rat has a censored time of 102 days, and the other untreated rat has a censored time of 104 days.
In this example, a litter is a cluster and the rats of the same litter are members of the cluster. Let Trt be a 0-1 variable representing the treatment a rat received, with value 1 for drug treatment and 0 otherwise. Data for the two litters of rats described earlier contribute six observations to the input data set:
Litter |
Time |
Status |
Trt |
1 |
101 |
1 |
1 |
1 |
49 |
0 |
0 |
1 |
104 |
1 |
0 |
3 |
104 |
0 |
1 |
3 |
102 |
0 |
0 |
3 |
104 |
0 |
0 |
The analysis of Lee, Wei, and Amato (1992) can be performed by PROC PHREG as follows:
proc phreg covs(aggregate); model Time*Status(0)=Treatment; id Litter; run;
Intensity and Rate/Mean Models for Recurrent Events Data
Suppose each subject experiences recurrences of the same phenomenon. Let 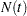 be the number of events a subject experiences over the interval [0,
be the number of events a subject experiences over the interval [0, ] and let
] and let 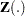 be the covariate process of the subject.
be the covariate process of the subject.
The intensity model (Andersen and Gill; 1982) is given by
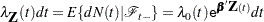 |
where 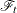 represents all the information of the processes
represents all the information of the processes 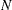 and
and 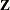 up to time
up to time  ,
, 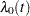 is an arbitrary baseline intensity function, and
is an arbitrary baseline intensity function, and 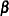 is the vector of regression coefficients. This model consists of two components: (1) all the influence of the prior events on future recurrences, if there is any, is mediated through the time-dependent covariates, and (2) the covariates have multiplicative effects on the instantaneous rate of the counting process. If the covariates are time invariant, the risk of recurrences is unaffected by the past events.
is the vector of regression coefficients. This model consists of two components: (1) all the influence of the prior events on future recurrences, if there is any, is mediated through the time-dependent covariates, and (2) the covariates have multiplicative effects on the instantaneous rate of the counting process. If the covariates are time invariant, the risk of recurrences is unaffected by the past events.
The proportional rates and means models (Pepe and Cai 1993; Lawless and Nadeau 1995; Lin et al. 2000) assume that the covariates have multiplicative effects on the mean and rate functions of the counting process. The rate function is given by
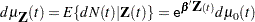 |
where 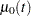 is an unknown continuous function and
is an unknown continuous function and 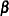 is the vector of regression parameters. If
is the vector of regression parameters. If 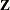 is time invariant, the mean function is given by
is time invariant, the mean function is given by
 |
For both the intensity and the proportional rates/means models, estimates of the regression coefficients are obtained by solving the partial likelihood score function. However, the covariance matrix estimate for the intensity model is computed as the inverse of the observed information matrix, while that for the proportional rates/means model is given by a sandwich estimate. For a given pattern of fixed covariates, the Nelson estimate for the cumulative intensity function is the same for the cumulative mean function, but their standard errors are not the same.
To fit the intensity or rate/mean model by using PROC PHREG, the counting process style of input is needed. A subject with  events contributes
events contributes  +1 observations to the input data set. The
+1 observations to the input data set. The 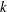 th observation of the subject identifies the time interval from the
th observation of the subject identifies the time interval from the  th event or time 0 (if
th event or time 0 (if 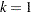 ) to the
) to the 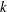 th event,
th event, 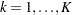 . The
. The 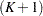 th observation represents the time interval from the
th observation represents the time interval from the 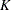 th event to time of censorship. The input data set should contain the following variables:
th event to time of censorship. The input data set should contain the following variables:
a TStart variable to represent the
 th recurrence time or the value 0 if
th recurrence time or the value 0 if 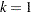
a TStop variable to represent the
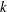 th recurrence time or the follow-up time if
th recurrence time or the follow-up time if 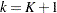
a Status variable indicating whether the TStop time is a recurrence time or a censored time; for example, Status=1 for a recurrence time and Status=0 for censored time
explanatory variables thought to be related to the recurrence times
If the rate/mean model is used, the input data should also contain an ID variable for identifying the subjects.
Consider the chronic granulomatous disease (CGD) data listed in Fleming and Harrington (1991). The disease is a rare disorder characterized by recurrent pyrogenic infections. The study is a placebo-controlled randomized clinical trial conducted by the International CGD Cooperative Study to assess the effect of gamma interferon to reduce the rate of infection. For each study patient the times of recurrent infections along with a number of prognostic factors were collected. For example:
Patient #17404, age 38, in the gamma interferon group had a follow-up time of 293 without any infection.
Patient #204001, age 12, in the placebo group had an infection at 219 days, a recurrent infection at 373 days, and was followed up to 414 days.
Let Trt be the variable representing the treatment status with value 1 for gamma interferon and value 2 for placebo. Let Age be a covariate representing the age of the CGD patient. Data for the two CGD patients described earlier are given in the following table.
ID |
TStart |
TStop |
Status |
Trt |
Age |
174054 |
0 |
293 |
0 |
1 |
38 |
204001 |
0 |
219 |
1 |
2 |
12 |
204001 |
219 |
373 |
1 |
2 |
12 |
204001 |
373 |
414 |
0 |
2 |
12 |
Since Patient #174054 had no infection through the end of the follow-up period (293 days), there is only one observation representing the period from time 0 to the end of the follow-up. Data for Patient #204001 are broken into three observations, since there are two infections. The first observation represents the period from time 0 to the first infection, the second observation represents the period from the first infection to the second infection, and the third time period represents the period from the second infection to the end of the follow-up.
The following specification fits the intensity model:
proc phreg; model (TStart,TStop)*Status(0)=Trt Age; run;
You can predict the cumulative intensity function for a given pattern of fixed covariates by specifying the CUMHAZ= option in the BASELINE statement. Suppose you are interested in two fixed patterns, one for patients of age 30 in the gamma interferon group and the other for patients of age 1 in the placebo group. You first create the SAS data set as follows:
data Pattern; Trt=1; Age=30; output; Trt=2; Age=1; output; run;
You then include the following BASELINE statement in the PROC PHREG specification. The CUMHAZ=_all_ option produces the cumulative hazard function estimates, the standard error estimates, and the lower and upper pointwise confidence limits.
baseline covariates=Pattern out=out1 cumhaz=_all_;
The following specification of PROC PHREG fits the mean model and predicts the cumulative mean function for the two patterns of covariates in the Pattern data set:
proc phreg covs(aggregate); model (Tstart,Tstop)*Status(0)=Trt Age; baseline covariates=Pattern out=out2 cmf=_all_; id ID;
The COV(AGGREGATE) option, along with the ID statement, computes the robust sandwich covariance matrix estimate. The CMF=_ALL_ option adds the cumulative mean function estimates, the standard error estimates, and the lower and upper pointwise confidence limits to the OUT=Out2 data set.
PWP Models for Recurrent Events Data
Let 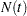 be the number of events a subject experiences by time
be the number of events a subject experiences by time  . Let
. Let 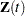 be the covariate vectors of the subject at time
be the covariate vectors of the subject at time  . For a subject who has
. For a subject who has 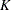 events before censorship takes place, let
events before censorship takes place, let 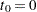 , let
, let 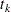 be the
be the 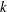 th recurrence time,
th recurrence time, 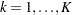 , and let
, and let 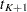 be the censored time. Prentice, Williams, and Peterson (1981) consider two time scales, a total time from the beginning of the study and a gap time from immediately preceding failure. The PWP models are stratified Cox-type models that allow the shape of the hazard function to depend on the number of preceding events and possibly on other characteristics of {
be the censored time. Prentice, Williams, and Peterson (1981) consider two time scales, a total time from the beginning of the study and a gap time from immediately preceding failure. The PWP models are stratified Cox-type models that allow the shape of the hazard function to depend on the number of preceding events and possibly on other characteristics of {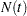 and
and 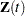 }. The total time and gap time models are given, respectively, as follows:
}. The total time and gap time models are given, respectively, as follows:
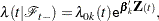 |
 |
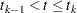 |
|||
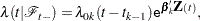 |
 |
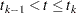 |
where 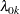 is an arbitrary baseline intensity functions, and
is an arbitrary baseline intensity functions, and 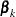 is a vector of stratum-specific regression coefficients. Here, a subject moves to the
is a vector of stratum-specific regression coefficients. Here, a subject moves to the 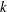 th stratum immediately after his
th stratum immediately after his  th recurrence time and remains there until the
th recurrence time and remains there until the 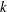 th recurrence occurs or until censorship takes place. For instance, a subject who experiences only one event moves from the first stratum to the second stratum after the event occurs and remains in the second stratum until the end of the follow-up.
th recurrence occurs or until censorship takes place. For instance, a subject who experiences only one event moves from the first stratum to the second stratum after the event occurs and remains in the second stratum until the end of the follow-up.
You can use PROC PHREG to carry out the analyses of the PWP models, but you have to prepare the input data set to provide the correct risk sets. The input data set for analyzing the total time is the same as the AG model with an additional variable to represent the stratum that the subject is in. A subject with 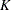 events contributes
events contributes 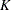 +1 observations to the input data set, one for each stratum that the subject moves to. The input data should contain the following variables:
+1 observations to the input data set, one for each stratum that the subject moves to. The input data should contain the following variables:
a TStart variable to represent the
 th recurrence time or the value 0 if
th recurrence time or the value 0 if 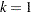
a TStop variable to represent the
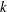 th recurrence time or the time of censorship if
th recurrence time or the time of censorship if 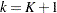
a Status variable with value 1 if the Time value is a recurrence time and value 0 if the Time value is a censored time
an Enum variable representing the index of the stratum that the subject is in. For a subject who has only one event at
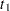 and is followed to time
and is followed to time 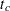 , Enum=1 for the first observation (where Time=
, Enum=1 for the first observation (where Time=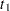 and Status=1) and Enum=2 for the second observation (where Time=
and Status=1) and Enum=2 for the second observation (where Time=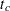 and Status=0).
and Status=0). explanatory variables thought to be related to the recurrence times
To analyze gap times, the input data set should also include a GapTime variable that is equal to (TStop  TStart).
TStart).
Consider the data of two subjects in CGD data described in the previous section:
Patients #174054, age 38, in the gamma interferon group had a follow-up time of 293 without any infection.
Patient #204001, age 12, in the placebo group had an infection at 219 days, a recurrent infection at 373 days, and a follow-up time of 414 days.
To illustrate, suppose all subjects have at most two observed events. The data for the two subjects in the input data set are as follows:
ID |
TStart |
TStop |
Gaptime |
Status |
Enum |
Trt |
Age |
174054 |
0 |
293 |
293 |
0 |
1 |
1 |
38 |
204001 |
0 |
219 |
219 |
1 |
1 |
2 |
12 |
204001 |
219 |
373 |
154 |
1 |
2 |
2 |
12 |
204001 |
373 |
414 |
41 |
0 |
3 |
2 |
12 |
Subject #174054 contributes only one observation to the input data, since there is no observed event. Subject #204001 contributes three observations, since there are two observed events.
To fit the total time model of PWP with stratum-specific slopes, either you can create the stratum-specific explanatory variables (Trt1, Trt2, and Trt3 for Trt, and Age1, Age2, and Age3 for Age) in a DATA step, or you can specify them in PROC PHREG by using programming statements as follows:
proc phreg; model (TStart,TStop)*Status(0)=Trt1 Trt2 Trt3 Age1 Age2 Age3; strata Enum; Trt1= Trt * (Enum=1); Trt2= Trt * (Enum=2); Trt3= Trt * (Enum=3); Age1= Age * (Enum=1); Age2= Age * (Enum=2); Age3= Age * (Enum=3); run;
To fit the total time model of PWP with the common regression coefficients, you specify the following:
proc phreg; model (TStart,TStop)*Status(0)=Trt Age; strata Enum; run;
To fit the gap time model of PWP with stratum-specific regression coefficients, you specify the following:
proc phreg; model Gaptime*Status(0)=Trt1 Trt2 Trt3 Age1 Age2 Age3; strata Enum; Trt1= Trt * (Enum=1); Trt2= Trt * (Enum=2); Trt3= Trt * (Enum=3); Age1= Age * (Enum=1); Age2= Age * (Enum=2); Age3= Age * (Enum=3); run;
To fit the gap time model of PWP with common regression coefficients, you specify the following:
proc phreg; model Gaptime*Status(0)=Trt Age; strata Enum; run;
Model Fit Statistics
Suppose the model contains 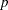 regression parameters. Let
regression parameters. Let 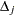 and
and 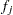 be the event indicator and the frequency, respectively, of the
be the event indicator and the frequency, respectively, of the 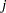 th observation. The three criteria displayed by the PHREG procedure are calculated as follows:
th observation. The three criteria displayed by the PHREG procedure are calculated as follows:
 2 Log Likelihood:
2 Log Likelihood: 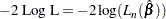
where
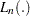 is a partial likelihood function for the corresponding TIES= option as described in the section Partial Likelihood Function for the Cox Model, and
is a partial likelihood function for the corresponding TIES= option as described in the section Partial Likelihood Function for the Cox Model, and 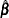 is the maximum likelihood estimate of the regression parameter vector.
is the maximum likelihood estimate of the regression parameter vector. Akaike’s Information Criterion:
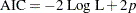
Schwarz Bayesian (Information) Criterion:
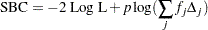
The  2 Log Likelihood statistic has a chi-square distribution under the null hypothesis (that all the explanatory effects in the model are zero) and the procedure produces a
2 Log Likelihood statistic has a chi-square distribution under the null hypothesis (that all the explanatory effects in the model are zero) and the procedure produces a 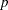 -value for this statistic. The AIC and SBC statistics give two different ways of adjusting the
-value for this statistic. The AIC and SBC statistics give two different ways of adjusting the  2 Log Likelihood statistic for the number of terms in the model and the number of observations used. These statistics should be used when comparing different models for the same data (for example, when you use the METHOD=STEPWISE option in the MODEL statement); lower values of the statistic indicate a more desirable model.
2 Log Likelihood statistic for the number of terms in the model and the number of observations used. These statistics should be used when comparing different models for the same data (for example, when you use the METHOD=STEPWISE option in the MODEL statement); lower values of the statistic indicate a more desirable model.
Residuals
This section describes the computation of residuals (RESMART=, RESDEV=, RESSCH=, and RESSCO=) in the OUTPUT statement.
First, consider TIES=BRESLOW. Let
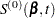 |
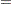 |
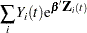 |
|||
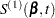 |
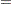 |
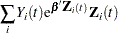 |
|||
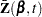 |
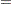 |
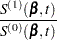 |
|||
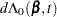 |
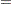 |
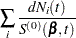 |
|||
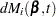 |
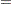 |
 |
The martingale residual at  is defined as
is defined as
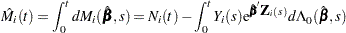 |
Here 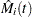 estimates the difference over
estimates the difference over 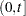 between the observed number of events for the
between the observed number of events for the  th subject and a conditional expected number of events. The quantity
th subject and a conditional expected number of events. The quantity 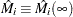 is referred to as the martingale residual for the
is referred to as the martingale residual for the  th subject. When the counting process MODEL specification is used, the RESMART= variable contains the component (
th subject. When the counting process MODEL specification is used, the RESMART= variable contains the component (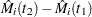 ) instead of the martingale residual at
) instead of the martingale residual at  . The martingale residual for a subject can be obtained by summing up these component residuals within the subject. For the Cox model with no time-dependent explanatory variables, the martingale residual for the
. The martingale residual for a subject can be obtained by summing up these component residuals within the subject. For the Cox model with no time-dependent explanatory variables, the martingale residual for the  th subject with observation time
th subject with observation time 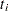 and event status
and event status 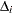 is
is
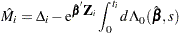 |
The deviance residuals 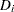 are a transform of the martingale residuals:
are a transform of the martingale residuals:
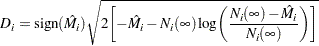 |
The square root shrinks large negative martingale residuals, while the logarithmic transformation expands martingale residuals that are close to unity. As such, the deviance residuals are more symmetrically distributed around zero than the martingale residuals. For the Cox model, the deviance residual reduces to the form
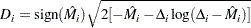 |
When the counting process MODEL specification is used, values of the RESDEV= variable are set to missing because the deviance residuals can be calculated only on a per-subject basis.
The Schoenfeld (1982) residual vector is calculated on a per-event-time basis. At the 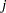 th event time
th event time 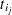 of the
of the  th subject, the Schoenfeld residual
th subject, the Schoenfeld residual
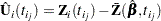 |
is the difference between the  th subject covariate vector at
th subject covariate vector at 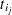 and the average of the covariate vectors over the risk set at
and the average of the covariate vectors over the risk set at 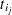 . Under the proportional hazards assumption, the Schoenfeld residuals have the sample path of a random walk; therefore, they are useful in assessing time trend or lack of proportionality. Harrell (1886) proposed a
. Under the proportional hazards assumption, the Schoenfeld residuals have the sample path of a random walk; therefore, they are useful in assessing time trend or lack of proportionality. Harrell (1886) proposed a  -transform of the Pearson correlation between these residuals and the rank order of the failure time as a test statistic for nonproportional hazards. Therneau, Grambsch, and Fleming (1990) considered a Kolmogorov-type test based on the cumulative sum of the residuals.
-transform of the Pearson correlation between these residuals and the rank order of the failure time as a test statistic for nonproportional hazards. Therneau, Grambsch, and Fleming (1990) considered a Kolmogorov-type test based on the cumulative sum of the residuals.
The score process for the  th subject at time
th subject at time  is
is
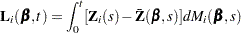 |
The vector 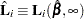 is the score residual for the
is the score residual for the  th subject. When the counting process MODEL specification is used, the RESSCO= variables contain the components of
th subject. When the counting process MODEL specification is used, the RESSCO= variables contain the components of 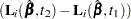 instead of the score process at
instead of the score process at  . The score residual for a subject can be obtained by summing up these component residuals within the subject.
. The score residual for a subject can be obtained by summing up these component residuals within the subject.
The score residuals are a decomposition of the first partial derivative of the log likelihood. They are useful in assessing the influence of each subject on individual parameter estimates. They also play an important role in the computation of the robust sandwich variance estimators of Lin and Wei (1989) and Wei, Lin, and Weissfeld (1989).
For TIES=EFRON, the preceding computation is modified to comply with the Efron partial likelihood. Consider an uncensored time t. For a given time  , let
, let 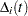 =1 if the
=1 if the  is an event time of the
is an event time of the  th subject and 0 otherwise. Let
th subject and 0 otherwise. Let 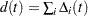 , which is the number of subjects that have an event at
, which is the number of subjects that have an event at  . For
. For 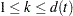 , let
, let
 |
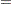 |
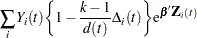 |
|||
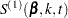 |
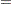 |
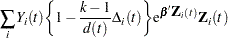 |
|||
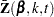 |
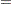 |
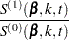 |
|||
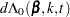 |
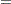 |
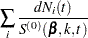 |
|||
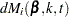 |
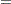 |
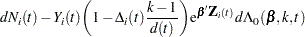 |
The martingale residual at  for the
for the  th subject is defined as
th subject is defined as
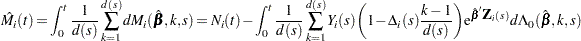 |
Deviance residuals are computed by using the same transform on the corresponding martingale residuals as in TIES=BRESLOW.
The Schoenfeld residual vector for the  th subject at event time
th subject at event time 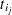 is
is
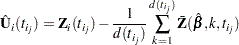 |
The score process for the  th subject at time
th subject at time  is given by
is given by
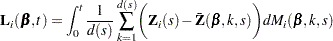 |
For TIES=DISCRETE or TIES=EXACT, it is difficult to come up with modifications that are consistent with the correponding partial likelihood. Residuals for these TIES= methods are computed by using the same formulae as in TIES=BRESLOW.
Diagnostics Based on Weighted Residuals
The vector of weighted Schoenfeld residuals, 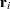 , is computed as
, is computed as
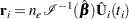 |
where 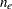 is the total number of events and
is the total number of events and 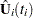 is the vector of Schoenfeld residuals at the event time
is the vector of Schoenfeld residuals at the event time 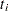 . The components of
. The components of 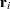 are output to the WTRESSCH= variables.
are output to the WTRESSCH= variables.
The weighted Schoenfeld residuals are useful in assessing the proportional hazards assumption. The idea is that most of the common alternatives to the proportional hazards can be cast in terms of a time-varying coefficient model
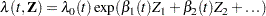 |
where 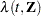 and
and 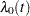 are hazard rates. Let
are hazard rates. Let 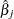 and
and 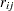 be the
be the 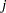 th component of
th component of 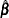 and
and 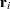 , respectively. Grambsch and Therneau (1994) suggest using a smoothed plot of (
, respectively. Grambsch and Therneau (1994) suggest using a smoothed plot of (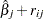 ) versus
) versus 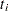 to discover the functional form of the time-varying coefficient
to discover the functional form of the time-varying coefficient 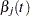 . A zero slope indicates that the coefficient is not varying with time.
. A zero slope indicates that the coefficient is not varying with time.
The weighted score residuals are used more often than their unscaled counterparts in assessing local influence. Let 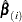 be the estimate of
be the estimate of 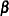 when the
when the  th subject is left out, and let
th subject is left out, and let 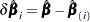 . The
. The 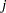 th component of
th component of 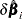 can be used to assess any untoward effect of the
can be used to assess any untoward effect of the  th subject on
th subject on 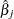 . The exact computation of
. The exact computation of 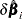 involves refitting the model each time a subject is omitted. Cain and Lange (1984) derived the following approximation of
involves refitting the model each time a subject is omitted. Cain and Lange (1984) derived the following approximation of 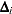 as weighted score residuals:
as weighted score residuals:
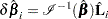 |
Here, 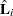 is the vector of the score residuals for the
is the vector of the score residuals for the  th subject. Values of
th subject. Values of 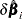 are output to the DFBETA= variables. Again, when the counting process MODEL specification is used, the DFBETA= variables contain the component
are output to the DFBETA= variables. Again, when the counting process MODEL specification is used, the DFBETA= variables contain the component 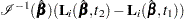 , where the score process
, where the score process 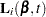 is defined in the section Residuals. The vector
is defined in the section Residuals. The vector 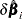 for the
for the  th subject can be obtained by summing these components within the subject.
th subject can be obtained by summing these components within the subject.
Note that these DFBETA statistics are a transform of the score residuals. In computing the robust sandwich variance estimators of Lin and Wei (1989) and Wei, Lin, and Weissfeld (1989), it is more convenient to use the DFBETA statistics than the score residuals (see Example 64.10).
Influence of Observations on Overall Fit of the Model
The LD statistic approximates the likelihood displacement, which is the amount by which minus twice the log likelihood (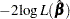 ), under a fitted model, changes when each subject in turn is left out. When the
), under a fitted model, changes when each subject in turn is left out. When the  th subject is omitted, the likelihood displacement is
th subject is omitted, the likelihood displacement is
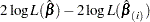 |
where 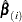 is the vector of parameter estimates obtained by fitting the model without the
is the vector of parameter estimates obtained by fitting the model without the  th subject. Instead of refitting the model without the
th subject. Instead of refitting the model without the  th subject, Pettitt and Bin Daud (1989) propose that the likelihood displacement for the
th subject, Pettitt and Bin Daud (1989) propose that the likelihood displacement for the  th subject be approximated by
th subject be approximated by
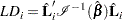 |
wher 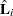 is the score residual vector of the
is the score residual vector of the  th subject. This approximation is output to the LD= variable.
th subject. This approximation is output to the LD= variable.
The LMAX statistic is another global influence statistic. This statistic is based on the symmetric matrix
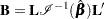 |
where 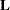 is the matrix with rows that are the score residual vectors
is the matrix with rows that are the score residual vectors 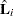 . The elements of the eigenvector associated with the largest eigenvalue of the matrix
. The elements of the eigenvector associated with the largest eigenvalue of the matrix 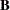 , standardized to unit length, give a measure of the sensitivity of the fit of the model to each observation in the data. The influence of the
, standardized to unit length, give a measure of the sensitivity of the fit of the model to each observation in the data. The influence of the  th subject on the global fit of the model is proportional to the magnitude of
th subject on the global fit of the model is proportional to the magnitude of 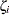 , where
, where 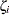 is the
is the  th element of the vector
th element of the vector 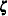 that satisfies
that satisfies
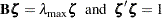 |
with 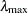 being the largest eigenvalue of
being the largest eigenvalue of 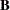 . The sign of
. The sign of 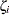 is irrelevant, and its absolute value is output to the LMAX= variable.
is irrelevant, and its absolute value is output to the LMAX= variable.
When the counting process MODEL specification is used, the LD= and LMAX= variables are set to missing, because these two global influence statistics can be calculated on a per-subject basis only.
Survivor Function Estimation for the Cox Model
Two estimators of the survivor function are available: one is the product-limit estimator (Kalbfleisch and Prentice; 1980, pp. 84–86) and the other is the Breslow (1972) estimator based on the empirical cumulative hazard function.
Product-Limit Estimates
Let 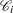 denote the set of individuals censored in the half-open interval
denote the set of individuals censored in the half-open interval 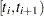 , where
, where 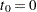 and
and 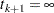 . Let
. Let  denote the censoring times in
denote the censoring times in 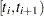 ; l ranges over
; l ranges over 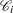 .
.
The likelihood function for all individuals is given by
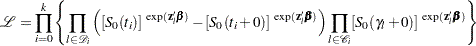 |
where 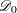 is empty. The likelihood
is empty. The likelihood 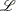 is maximized by taking
is maximized by taking 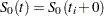 for
for 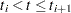 and allowing the probability mass to fall only on the observed event times
and allowing the probability mass to fall only on the observed event times 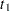 ,
,  ,
, 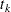 . By considering a discrete model with hazard contribution
. By considering a discrete model with hazard contribution 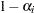 at
at 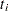 , you take
, you take 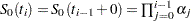 , where
, where 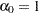 . Substitution into the likelihood function produces
. Substitution into the likelihood function produces
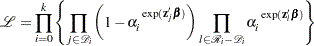 |
If you replace 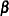 with
with 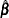 estimated from the partial likelihood function and then maximize with respect to
estimated from the partial likelihood function and then maximize with respect to 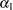 ,
,  ,
,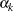 , the maximum likelihood estimate
, the maximum likelihood estimate 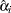 of
of  becomes a solution of
becomes a solution of
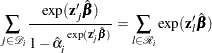 |
When only a single failure occurs at 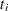 ,
, 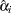 can be found explicitly. Otherwise, an iterative solution is obtained by the Newton method.
can be found explicitly. Otherwise, an iterative solution is obtained by the Newton method.
The estimated baseline cumulative hazard function is
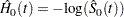 |
where 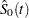 is the estimated baseline survivor function given by
is the estimated baseline survivor function given by
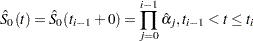 |
For details, refer to Kalbfleisch and Prentice (1980). For a given realization of the explanatory variables 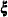 , the product-limit estimate of the survival function at
, the product-limit estimate of the survival function at 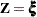 is
is
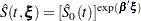 |
Empirical Cumulative Hazards Function Estimates
Let 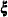 be a given realization of the explanatory variables. The empirical cumulative hazard function estimate at
be a given realization of the explanatory variables. The empirical cumulative hazard function estimate at 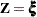 is
is
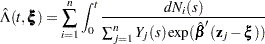 |
The variance estimator of 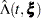 is given by the following (Tsiatis; 1981):
is given by the following (Tsiatis; 1981):
 |
 |
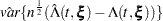 |
|||
 |
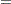 |
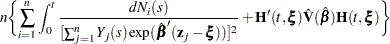 |
where 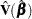 is the estimated covariance matrix of
is the estimated covariance matrix of 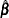 and
and
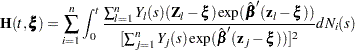 |
For the marginal model, the variance estimator computation follows Spiekerman and Lin (1998).
The empirical cumulative hazard function (CH) estimate of the survivor function for 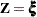 is
is
 |
Confidence Intervals for the Survivor Function
Let 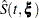 and
and 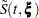 correspond to the product-limit (PL) and empirical cumulative hazard function (CH) estimates of the survivor function for
correspond to the product-limit (PL) and empirical cumulative hazard function (CH) estimates of the survivor function for 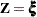 , respectively. Both the standard error of log(
, respectively. Both the standard error of log(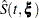 ) and the standard error of log(
) and the standard error of log(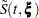 ) are approximated by
) are approximated by 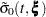 , which is the square root of the variance estimate of
, which is the square root of the variance estimate of 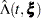 ; refer to Kalbfleisch and Prentice (1980, p. 116). By the delta method, the standard errors of
; refer to Kalbfleisch and Prentice (1980, p. 116). By the delta method, the standard errors of 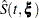 and
and 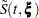 are given by
are given by
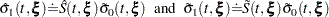 |
respectively. The standard errors of log[–log(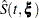 )] and log[–log(
)] and log[–log(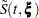 )] are given by
)] are given by
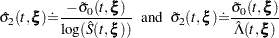 |
respectively.
Let  be the upper
be the upper 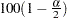 percentile point of the standard normal distribution. A
percentile point of the standard normal distribution. A 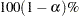 confidence interval for the survivor function
confidence interval for the survivor function 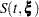 is given in the following table.
is given in the following table.
CLTYPE |
Method |
Confidence Limits |
|---|---|---|
LOG |
PL |
|
LOG |
CH |
|
LOGLOG |
PL |
|
LOGLOG |
CH |
|
NORMAL |
PL |
|
NORMAL |
CH |
|
Effect Selection Methods
Five effect selection methods are available. The simplest method (and the default) is SELECTION=NONE, for which PROC PHREG fits the complete model as specified in the MODEL statement. The other four methods are FORWARD for forward selection, BACKWARD for backward elimination, STEPWISE for stepwise selection, and SCORE for best subsets selection. These methods are specified with the SELECTION= option in the MODEL statement and are based on the score test or Wald test as described in the section Type 3 Tests.
When SELECTION=FORWARD, PROC PHREG first estimates parameters for effects that are forced into the model. These are the first  effects in the MODEL statement, where
effects in the MODEL statement, where  is the number specified by the START= or INCLUDE= option in the MODEL statement (
is the number specified by the START= or INCLUDE= option in the MODEL statement ( is zero by default). Next, the procedure computes the score statistic for each effect that is not in the model. Each score statistic is the chi-square statistic of the score test for testing the null hypothesis that the corresponding effect that is not in the model is null. If the largest of these statistics is significant at the SLSENTRY= level, the effect with the largest score statistic is added to the model. After an effect is entered in the model, it is never removed from the model. The process is repeated until none of the remaining effects meet the specified level for entry or until the STOP= value is reached.
is zero by default). Next, the procedure computes the score statistic for each effect that is not in the model. Each score statistic is the chi-square statistic of the score test for testing the null hypothesis that the corresponding effect that is not in the model is null. If the largest of these statistics is significant at the SLSENTRY= level, the effect with the largest score statistic is added to the model. After an effect is entered in the model, it is never removed from the model. The process is repeated until none of the remaining effects meet the specified level for entry or until the STOP= value is reached.
When SELECTION=BACKWARD, parameters for the complete model as specified in the MODEL statement are estimated unless the START= option is specified. In that case, only the parameters for the first  effects in the MODEL statement are estimated, where
effects in the MODEL statement are estimated, where  is the number specified by the START= option. Next, the procedure computes the Wald statistic of each effect in the model. Each Wald’s statistic is the chi-square statistic of the Wald test for testing the null hypothesis that the corresponding effect is null. If the smallest of these statistics is not significiant at the SLSTAY= level, the effect with the smallest Wald statistic is removed. After an effect is removed from the model, it remains excluded. The process is repeated until no other variable in the model meets the specified level for removal or until the STOP= value is reached.
is the number specified by the START= option. Next, the procedure computes the Wald statistic of each effect in the model. Each Wald’s statistic is the chi-square statistic of the Wald test for testing the null hypothesis that the corresponding effect is null. If the smallest of these statistics is not significiant at the SLSTAY= level, the effect with the smallest Wald statistic is removed. After an effect is removed from the model, it remains excluded. The process is repeated until no other variable in the model meets the specified level for removal or until the STOP= value is reached.
The SELECTION=STEPWISE option is similar to the SELECTION=FORWARD option except that effects already in the model do not necessarily remain. Effects are entered into and removed from the model in such a way that each forward selection step can be followed by one or more backward elimination steps. The stepwise selection process terminates if no further effect can be added to the model or if the effect just entered into the model is the only effect that is removed in the subsequent backward elimination.
For SELECTION=SCORE, PROC PHREG uses the branch-and-bound algorithm of Furnival and Wilson (1974) to find a specified number of models with the highest score (chi-square) statistic for all possible model sizes, from 1, 2, or 3 variables, and so on, up to the single model that contains all of the explanatory variables. The number of models displayed for each model size is controlled by the BEST= option. You can use the START= option to impose a minimum model size, and you can use the STOP= option to impose a maximum model size. For instance, with BEST=3, START=2, and STOP=5, the SCORE selection method displays the best three models (that is, the three models with the highest score chi-squares) that contain 2, 3, 4, and 5 variables. One of the limitations of the branch-and-bound algorithm is that it works only when each explanatory effect contains exactly one parameter—the SELECTION=SCORE option is not allowed when an explanatory effect in the MODEL statement contains a CLASS variable.
The SEQUENTIAL and STOPRES options can alter the default criteria for adding variables to or removing variables from the model when they are used with the FORWARD, BACKWARD, or STEPWISE selection method.
Assessment of the Proportional Hazards Model
The proportional hazards model specifies that the hazard function for the failure time 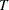 associated with a
associated with a 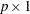 column covariate vector
column covariate vector 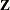 takes the form
takes the form
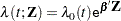 |
where 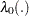 is an unspecified baseline hazard function and
is an unspecified baseline hazard function and 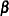 is a
is a 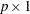 column vector of regression parameters. Lin, Wei, and Ying (1993) present graphical and numerical methods for model assessment based on the cumulative sums of martingale residuals and their transforms over certain coordinates (such as covariate values or follow-up times). The distributions of these stochastic processes under the assumed model can be approximated by the distributions of certain zero-mean Gaussian processes whose realizations can be generated by simulation. Each observed residual pattern can then be compared, both graphically and numerically, with a number of realizations from the null distribution. Such comparisons enable you to assess objectively whether the observed residual pattern reflects anything beyond random fluctuation. These procedures are useful in determining appropriate functional forms of covariates and assessing the proportional hazards assumption. You use the ASSESS statement to carry out these model-checking procedures.
column vector of regression parameters. Lin, Wei, and Ying (1993) present graphical and numerical methods for model assessment based on the cumulative sums of martingale residuals and their transforms over certain coordinates (such as covariate values or follow-up times). The distributions of these stochastic processes under the assumed model can be approximated by the distributions of certain zero-mean Gaussian processes whose realizations can be generated by simulation. Each observed residual pattern can then be compared, both graphically and numerically, with a number of realizations from the null distribution. Such comparisons enable you to assess objectively whether the observed residual pattern reflects anything beyond random fluctuation. These procedures are useful in determining appropriate functional forms of covariates and assessing the proportional hazards assumption. You use the ASSESS statement to carry out these model-checking procedures.
For a sample of  subjects, let
subjects, let 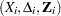 be the data of the
be the data of the  th subject; that is,
th subject; that is, 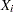 represents the observed failure time,
represents the observed failure time, 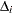 has a value of 1 if
has a value of 1 if 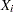 is an uncensored time and 0 otherwise, and
is an uncensored time and 0 otherwise, and 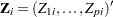 is a
is a 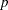 -vector of covariates. Let
-vector of covariates. Let 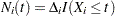 and
and 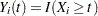 . Let
. Let
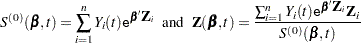 |
Let 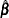 be the maximum partial likelihood estimate of
be the maximum partial likelihood estimate of 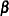 , and let
, and let 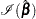 be the observed information matrix.
be the observed information matrix.
The martingale residuals are defined as
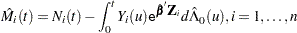 |
where 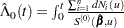 .
.
The empirical score process 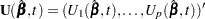 is a transform of the martingale residuals:
is a transform of the martingale residuals:
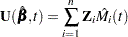 |
Checking the Functional Form of a Covariate
To check the functional form of the 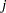 th covariate, consider the partial-sum process of
th covariate, consider the partial-sum process of 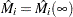 :
:
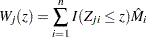 |
Under that null hypothesis that the model holds, 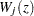 can be approximated by the zero-mean Gaussian process
can be approximated by the zero-mean Gaussian process
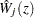 |
 |
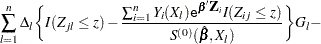 |
|||
 |
 |
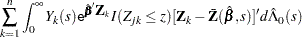 |
|||
 |
 |
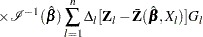 |
where 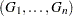 are independent standard normal variables that are independent of
are independent standard normal variables that are independent of  ,
, 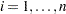 .
.
You can assess the functional form of the 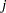 th covariate by plotting a small number of realizations (the default is 20) of
th covariate by plotting a small number of realizations (the default is 20) of 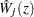 on the same graph as the observed
on the same graph as the observed 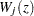 and visually comparing them to see how typical the observed pattern of
and visually comparing them to see how typical the observed pattern of 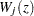 is of the null distribution samples. You can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let
is of the null distribution samples. You can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let 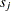 be the observed value of
be the observed value of 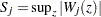 and let
and let 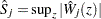 . The
. The 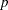 -value
-value 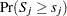 is approximated by
is approximated by 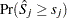 , which in turn is approximated by generating a large number of realizations (1000 is the default) of
, which in turn is approximated by generating a large number of realizations (1000 is the default) of 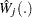 .
.
Checking the Proportional Hazards Assumption
Consider the standardized empirical score process for the 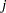 th component of
th component of 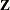
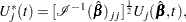 |
Under the null hypothesis that the model holds, 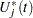 can be approximated by
can be approximated by
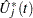 |
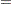 |
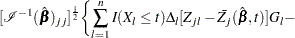 |
|||
 |
 |
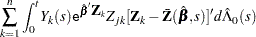 |
|||
 |
 |
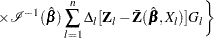 |
where 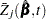 is the
is the 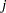 th component of
th component of 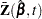 , and
, and 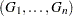 are independent standard normal variables that are independent of
are independent standard normal variables that are independent of 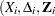 ,
,  .
.
You can assess the proportional hazards assumption for the 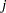 th covariate by plotting a few realizations of
th covariate by plotting a few realizations of 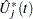 on the same graph as the observed
on the same graph as the observed 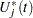 and visually comparing them to see how typical the observed pattern of
and visually comparing them to see how typical the observed pattern of 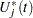 is of the null distribution samples. Again you can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let
is of the null distribution samples. Again you can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let 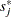 be the observed value of
be the observed value of 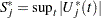 and let
and let 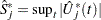 . The
. The 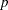 -value
-value 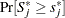 is approximated by
is approximated by 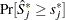 , which in turn is approximated by generating a large number of realizations (1000 is the default) of
, which in turn is approximated by generating a large number of realizations (1000 is the default) of 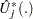 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.