| The GENMOD Procedure |
Example 37.10 Bayesian Analysis of a Poisson Regression Model
This example illustrates a Bayesian analysis of a log-linear Poisson regression model. Consider the following data on patients from clinical trials. The data set is a subset of the data described in Ibrahim, Chen, and Lipsitz (1999).
data Liver; input X1-X6 Y; datalines; 19.1358 50.0110 51.000 0 0 1 3 23.5970 18.4959 3.429 0 0 1 9 20.0474 56.7699 3.429 1 1 0 6 28.0277 59.7836 4.000 0 0 1 6 28.6851 74.1589 5.714 1 0 1 1 18.8092 31.0630 2.286 0 1 1 61 28.7201 52.9178 37.286 1 0 1 6 21.3669 61.6603 54.143 0 1 1 6 23.7332 42.2904 0.571 1 0 1 21 ... more lines ... 19.1327 65.3425 2.571 1 0 0 1 17.3010 51.4493 4.429 1 0 0 6 ; run;
The primary interest is in prediction of the number of cancerous liver nodes when a patient enters the trials, by using six other baseline characteristics. The number of nodes is modeled by a Poisson regression model with the six baseline characteristics as covariates. The response and regression variables are as follows:
Y |
Number of Cancerous Liver Nodes |
X1 |
Body Mass Index |
X2 |
Age, in Years |
X3 |
Time Since Diagnosis of Disease, in Weeks |
X4 |
Two Biochemical Markers (each classified as normal=1 or abnormal=0) |
X5 |
Anti Hepatitis B Antigen |
X6 |
Associated Jaundice (yes=1, no=0) |
Two analyses are performed using PROC GENMOD. The first analysis uses noninformative normal prior distributions, and the second analysis uses an informative normal prior for one of the regression parameters.
In the following BAYES statement, COEFFPRIOR=NORMAL specifies a noninformative independent normal prior distribution with zero mean and variance 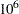 for each parameter.
for each parameter.
The initial analysis is performed using PROC GENMOD to obtain Bayesian estimates of the regression coefficients by using the following SAS statements:
ods graphics ON; proc genmod data=Liver; model Y = X1-X6 / dist=Poisson link=log; bayes seed=1 coeffprior=normal; run;
Maximum likelihood estimates of the model parameters are computed by default. These are shown in the "Analysis of Maximum Likelihood Parameter Estimates" table in Output 37.10.1.
| Analysis Of Maximum Likelihood Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | |
| Intercept | 1 | 2.4508 | 0.2284 | 2.0032 | 2.8984 |
| X1 | 1 | -0.0044 | 0.0080 | -0.0201 | 0.0114 |
| X2 | 1 | -0.0135 | 0.0024 | -0.0181 | -0.0088 |
| X3 | 1 | -0.0029 | 0.0022 | -0.0072 | 0.0014 |
| X4 | 1 | -0.2715 | 0.0795 | -0.4272 | -0.1157 |
| X5 | 1 | 0.3215 | 0.0832 | 0.1585 | 0.4845 |
| X6 | 1 | 0.2077 | 0.0827 | 0.0456 | 0.3698 |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 |
| Note: | The scale parameter was held fixed. |
Noninformative independent normal prior distributions with zero means and variances of 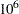 were used in the initial analysis. These are shown in Output 37.10.2.
were used in the initial analysis. These are shown in Output 37.10.2.
Initial values for the Markov chain are listed in the "Initial Values and Seeds" table in Output 37.10.3. The random number seed is also listed so that you can reproduce the analysis. Since no seed was specified, the seed shown was derived from the time of day.
Summary statistics for the posterior sample are displayed in the "Fit Statistics," "Descriptive Statistics for the Posterior Sample," "Interval Statistics for the Posterior Sample," and "Posterior Correlation Matrix" tables in Output 37.10.4, Output 37.10.5, Output 37.10.6, and Output 37.10.7, respectively. Since noninformative prior distributions for the regression coefficients were used, the mean and standard deviations of the posterior distributions for the model parameters are close to the maximum likelihood estimates and standard errors.
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 10000 | 2.4520 | 0.2268 | 2.2997 | 2.4521 | 2.6053 |
| X1 | 10000 | -0.00473 | 0.00801 | -0.0100 | -0.00465 | 0.000759 |
| X2 | 10000 | -0.0134 | 0.00236 | -0.0150 | -0.0134 | -0.0118 |
| X3 | 10000 | -0.00309 | 0.00220 | -0.00455 | -0.00305 | -0.00158 |
| X4 | 10000 | -0.2705 | 0.0792 | -0.3241 | -0.2697 | -0.2172 |
| X5 | 10000 | 0.3193 | 0.0834 | 0.2629 | 0.3180 | 0.3762 |
| X6 | 10000 | 0.2095 | 0.0834 | 0.1538 | 0.2086 | 0.2653 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | 2.0169 | 2.9056 | 2.0069 | 2.8923 |
| X1 | 0.050 | -0.0210 | 0.0106 | -0.0212 | 0.0103 |
| X2 | 0.050 | -0.0181 | -0.00878 | -0.0181 | -0.00885 |
| X3 | 0.050 | -0.00757 | 0.00109 | -0.00764 | 0.000989 |
| X4 | 0.050 | -0.4250 | -0.1132 | -0.4232 | -0.1119 |
| X5 | 0.050 | 0.1552 | 0.4821 | 0.1647 | 0.4905 |
| X6 | 0.050 | 0.0477 | 0.3749 | 0.0490 | 0.3758 |
| Posterior Correlation Matrix | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Intercept | X1 | X2 | X3 | X4 | X5 | X6 |
| Intercept | 1.000 | -0.705 | -0.430 | -0.046 | -0.225 | -0.180 | -0.415 |
| X1 | -0.705 | 1.000 | -0.211 | -0.013 | -0.068 | 0.067 | 0.128 |
| X2 | -0.430 | -0.211 | 1.000 | -0.006 | 0.070 | 0.057 | 0.118 |
| X3 | -0.046 | -0.013 | -0.006 | 1.000 | 0.016 | -0.055 | -0.089 |
| X4 | -0.225 | -0.068 | 0.070 | 0.016 | 1.000 | -0.011 | 0.089 |
| X5 | -0.180 | 0.067 | 0.057 | -0.055 | -0.011 | 1.000 | -0.042 |
| X6 | -0.415 | 0.128 | 0.118 | -0.089 | 0.089 | -0.042 | 1.000 |
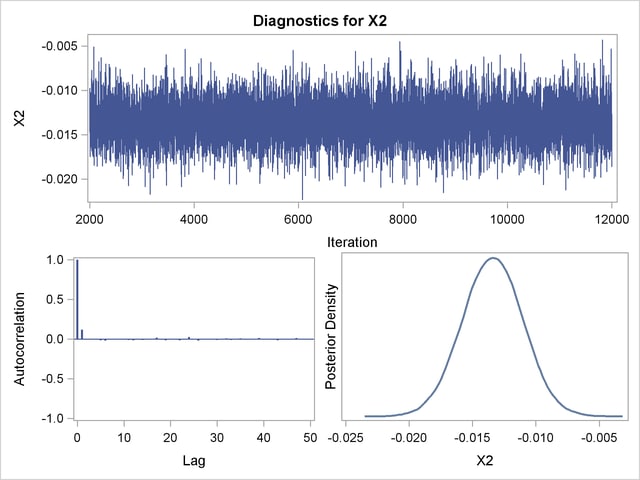
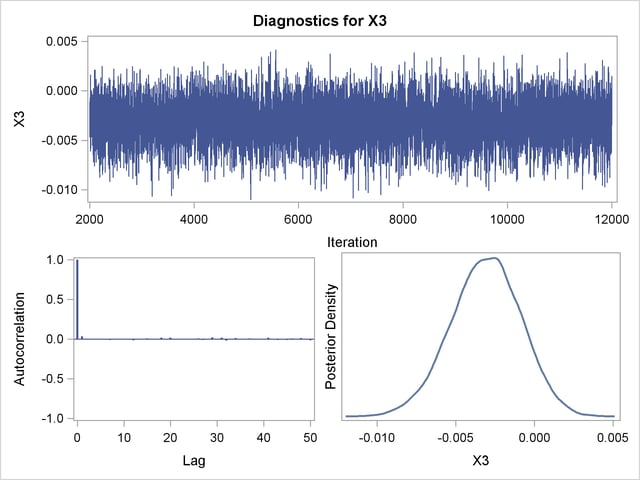
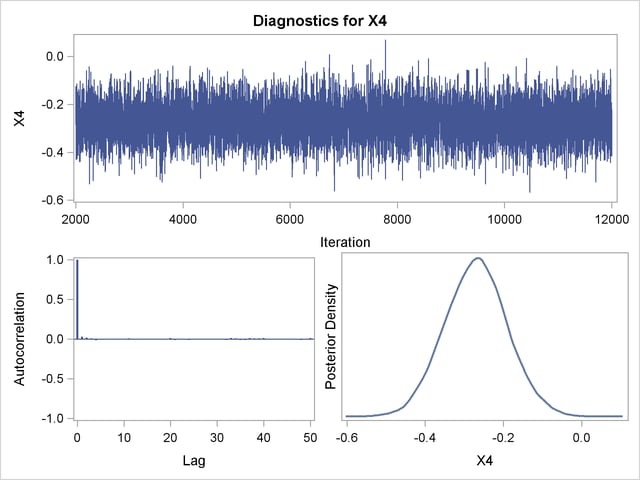
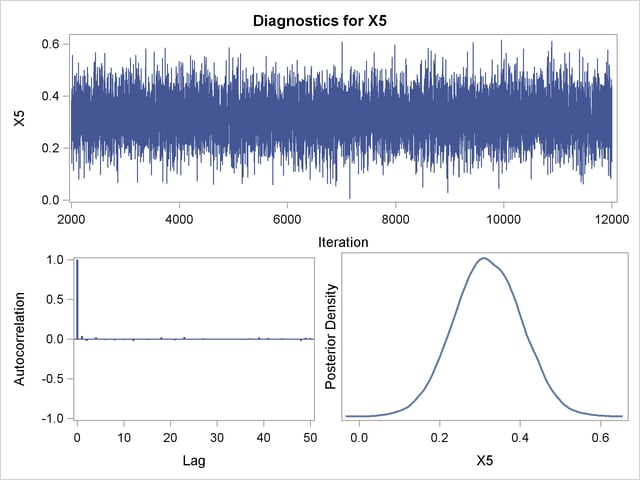
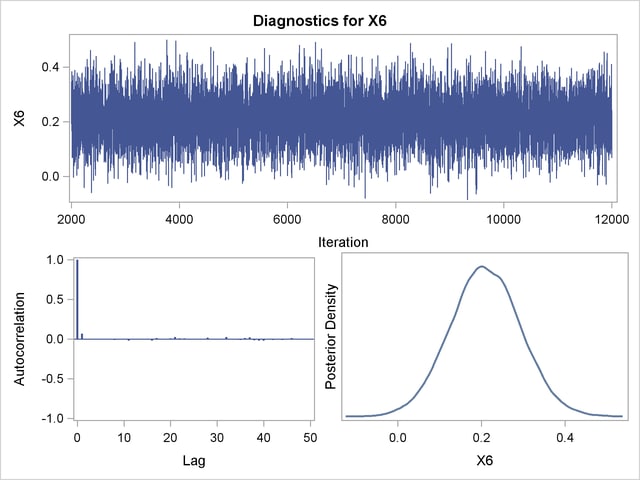
Posterior sample autocorrelations for each model parameter are shown in Output 37.10.8. The autocorrelation after 10 lags is negligible for all parameters, indicating good mixing in the Markov chain.
| Posterior Autocorrelations | ||||
|---|---|---|---|---|
| Parameter | Lag 1 | Lag 5 | Lag 10 | Lag 50 |
| Intercept | 0.0551 | -0.0134 | -0.0101 | 0.0012 |
| X1 | 0.0894 | -0.0054 | -0.0080 | 0.0019 |
| X2 | 0.1197 | -0.0170 | 0.0061 | 0.0006 |
| X3 | 0.0324 | -0.0036 | -0.0033 | -0.0160 |
| X4 | 0.0309 | 0.0056 | 0.0053 | 0.0115 |
| X5 | 0.0402 | 0.0015 | -0.0111 | 0.0123 |
| X6 | 0.0696 | -0.0047 | -0.0024 | 0.0006 |
The p-values for the Geweke test statistics shown in Output 37.10.9 all indicate convergence of the MCMC. See the section Assessing Markov Chain Convergence for more information about convergence diagnostics and their interpretation.
The effective sample sizes for each parameter are shown in Output 37.10.10.
Trace, autocorrelation, and density plots for the seven model parameters are shown in Output 37.10.11 through Output 37.10.17. All indicate satisfactory convergence of the Markov chain.
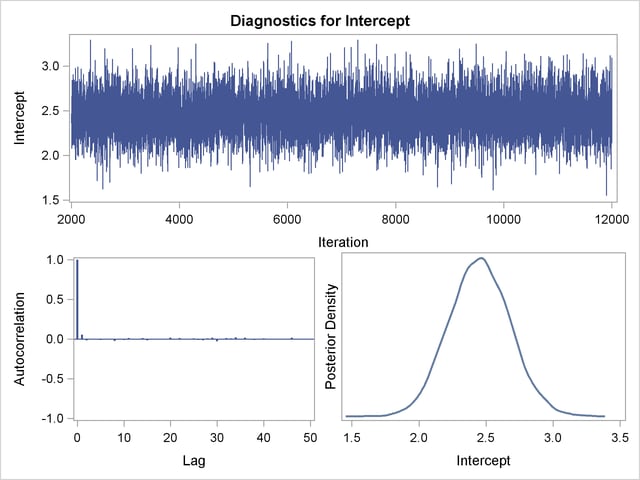
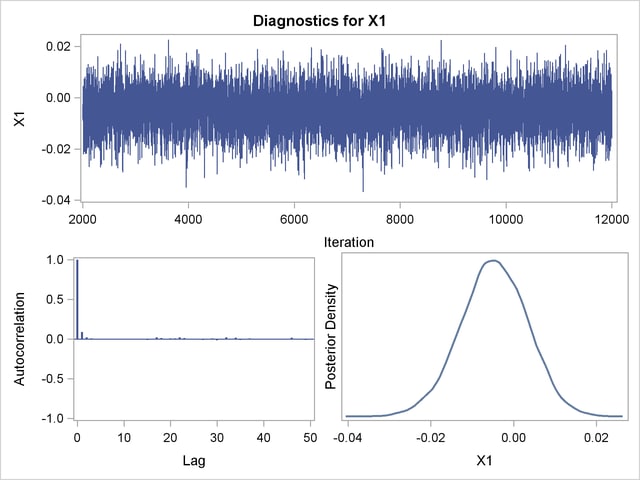
In order to illustrate the use of an informative prior distribution, suppose that researchers expect that a unit increase in body mass index (X1) will be associated with an increase in the mean number of nodes of between 10% and 20%, and they want to incorporate this prior knowledge in the Bayesian analysis. For log-linear models, the mean and linear predictor are related by 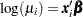 . If
. If 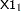 and
and 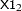 are two values of body mass index,
are two values of body mass index,  and
and 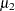 are the two mean values, and all other covariates remain equal for the two values of X1, then
are the two mean values, and all other covariates remain equal for the two values of X1, then
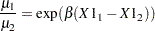 |
so that for a unit change in X1,
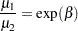 |
If 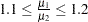 , then
, then 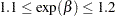 , or
, or 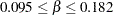 . This gives you guidance in specifying a prior distribution for the
. This gives you guidance in specifying a prior distribution for the 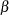 for body mass index. Taking the mean of the prior normal distribution to be the midrange of the values of
for body mass index. Taking the mean of the prior normal distribution to be the midrange of the values of 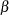 , and taking
, and taking 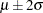 to be the extremes of the range, an
to be the extremes of the range, an 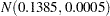 is the resulting prior distribution. The second analysis uses this informative normal prior distribution for the coefficient of
is the resulting prior distribution. The second analysis uses this informative normal prior distribution for the coefficient of  and uses independent noninformative normal priors with zero means and variances equal to
and uses independent noninformative normal priors with zero means and variances equal to 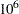 for the remaining model regression parameters.
for the remaining model regression parameters.
In the following BAYES statement, COEFFPRIOR=NORMAL(INPUT=NormalPrior) specifies the normal prior distribution for the regression coefficients with means and variances contained in the data set NormalPrior.
An analysis is performed using PROC GENMOD to obtain Bayesian estimates of the regression coefficients by using the following SAS statements:
data NormalPrior; input _type_ $ Intercept X1-X6; datalines; Var 1e6 0.0005 1e6 1e6 1e6 1e6 1e6 Mean 0.0 0.1385 0.0 0.0 0.0 0.0 0.0 ; run;
proc genmod data=Liver; model Y = X1-X6 / dist=Poisson link=log; bayes seed=1 plots=none coeffprior=normal(input=NormalPrior) ; run; ods graphics off;
The prior distributions for the regression parameters are shown in Output 37.10.18.
Initial values for the MCMC are shown in Output 37.10.19. The initial values of the covariates are joint estimates of their posterior modes. The prior distribution for X1 is informative, so the initial value of X1 is further from the MLE than the rest of the covariates. Initial values for the rest of the covariates are close to their MLEs, since noninformative prior distributions were specified for them.
Goodness-of-fit, summary, and interval statistics are shown in Output 37.10.20. Except for X1, the statistics shown in Output 37.10.20 are very similar to the previous statistics for noninformative priors shown in Output 37.10.4 through Output 37.10.7. The point estimate for X1 is now positive. This is expected because the prior distribution on 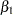 is quite informative. The distribution reflects the belief that the coefficient is positive. The
is quite informative. The distribution reflects the belief that the coefficient is positive. The 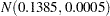 distribution places the majority of its probability density on positive values. As a result, the posterior density of
distribution places the majority of its probability density on positive values. As a result, the posterior density of 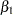 places more likelihood on positive values than in the noninformative case.
places more likelihood on positive values than in the noninformative case.
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 10000 | 2.1393 | 0.2160 | 1.9929 | 2.1417 | 2.2845 |
| X1 | 10000 | 0.0104 | 0.00685 | 0.00583 | 0.0106 | 0.0151 |
| X2 | 10000 | -0.0143 | 0.00236 | -0.0159 | -0.0143 | -0.0127 |
| X3 | 10000 | -0.00318 | 0.00218 | -0.00463 | -0.00313 | -0.00170 |
| X4 | 10000 | -0.2801 | 0.0798 | -0.3342 | -0.2807 | -0.2258 |
| X5 | 10000 | 0.3336 | 0.0834 | 0.2772 | 0.3337 | 0.3902 |
| X6 | 10000 | 0.2333 | 0.0822 | 0.1791 | 0.2327 | 0.2892 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | 1.7161 | 2.5599 | 1.7075 | 2.5507 |
| X1 | 0.050 | -0.00323 | 0.0236 | -0.00264 | 0.0241 |
| X2 | 0.050 | -0.0189 | -0.00960 | -0.0189 | -0.00972 |
| X3 | 0.050 | -0.00754 | 0.00101 | -0.00754 | 0.000963 |
| X4 | 0.050 | -0.4348 | -0.1223 | -0.4311 | -0.1196 |
| X5 | 0.050 | 0.1705 | 0.4970 | 0.1661 | 0.4915 |
| X6 | 0.050 | 0.0696 | 0.3968 | 0.0655 | 0.3904 |
Copyright © SAS Institute, Inc. All Rights Reserved.