The COSAN modeling language in PROC CALIS enables you to specify the direct or implied mean and covariance structures for the data in terms of matrix formulas. It is a very general modeling language, and all other modeling languages in PROC CALIS are special cases of the COSAN modeling language. This example shows how you can apply the COSAN modeling language to situations where you might usually use the "easier" modeling languages. Therefore, the purpose of this example is not to recommend the use of the COSAN modeling specification to the specific application. Rather, through its connections with other more well-known model types, this example intends to help you understand the basics of the COSAN modeling language.
Emulating the RAM model by the COSAN Modeling Language
In the RAM model, you specify all information regarding the path effects or coefficients (that is, single-headed arrows in the path diagram) in the so-called  (_A_) matrix. You specify all the information regarding the variances and covariances (that is, the double-headed arrows in the path diagram) in the
(_A_) matrix. You specify all the information regarding the variances and covariances (that is, the double-headed arrows in the path diagram) in the  (_P_) matrix. See the section The RAM Model for more details about the mathematical model for RAM. Once you define these two matrices, the implied covariance structures for the observed variables are derived by the formula
(_P_) matrix. See the section The RAM Model for more details about the mathematical model for RAM. Once you define these two matrices, the implied covariance structures for the observed variables are derived by the formula
where  is an identity matrix and
is an identity matrix and  is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables.
is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables.
For example, in the RAM model specification in Example 25.20, you essentially use the following RAM model specification:
proc calis nobs=932 data=Wheaton primat nose;
ram
var = Anomie67 /* 1 */
Powerless67 /* 2 */
Anomie71 /* 3 */
Powerless71 /* 4 */
Education /* 5 */
SEI /* 6 */
Alien67 /* 7 */
Alien71 /* 8 */
SES, /* 9 */
_A_ 1 7 1.0,
_A_ 2 7 0.833,
_A_ 3 8 1.0,
_A_ 4 8 0.833,
_A_ 5 9 1.0,
_A_ 6 9 lambda,
_A_ 7 9 gamma1,
_A_ 8 9 gamma2,
_A_ 8 7 beta,
_P_ 1 1 theta1,
_P_ 2 2 theta2,
_P_ 3 3 theta1,
_P_ 4 4 theta2,
_P_ 5 5 theta3,
_P_ 6 6 theta4,
_P_ 7 7 psi1,
_P_ 8 8 psi2,
_P_ 9 9 phi,
_P_ 1 3 theta5,
_P_ 2 4 theta5;
run;
In the RAM statement, you specify all the parameters in the _A_ and _P_ matrices, and PROC CALIS generates the corresponding covariance structures for analysis. However, with the COSAN modeling language, in addition to the parameter in the model matrices, you need to supply the matrix formula for the covariance structures, as shown in the preceding formula for 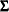 .
.
Before discussing how you can specify the COSAN model that corresponds to this RAM model specification, it is useful to look at the initial model matrices that are generated by the preceding RAM model specification. To do this, you use the PRIMAT option in the PROC CALIS statement.
Output 25.26.1 and Output 25.26.2 show the initial _A_ and _P_ matrices, respectively, for the RAM model.
Output 25.26.1
Initial _A_ Matrix of the RAM Model
Output 25.26.2
Initial _P_ Matrix of the RAM Model
Essentially, to specify the same model by the COSAN modeling language, you need to provide the same information in these two initial model matrices and the covariance structure formula for 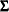 in the COSAN model specification, which is shown in the following statements:
in the COSAN model specification, which is shown in the following statements:
proc calis data=Wheaton nobs=932 nose;
cosan
var= Anomie67 Powerless67 Anomie71 Powerless71 Education SEI,
J(9, IDE) * A(9, GEN, IMI) * P(9, SYM);
matrix A
[1 2 8 , 7] = 1.0 0.833 beta,
[3 4 , 8] = 1.0 0.833 ,
[5 6 7 8 , 9] = 1. lambda gamma1 gamma2;
matrix P
[1,1] = theta1-theta2 theta1-theta4 ,
[7,7] = psi1 psi2 phi,
[3,1] = theta5 ,
[4,2] = theta5 ;
vnames
J = [Anomie67 Powerless67 Anomie71 Powerless71
Education SEI Alien67 Alien71 SES],
A = J,
P = A;
run;
In the PROC CALIS statement, you provide the data set in the DATA= option and the number of observations in the NOBS= option. You use the NOSE option to turn off the computation of the standard error estimates.
In the VAR= option of the COSAN statement, you provide the list of observed variables for the analysis. You do not specify the latent variables in the VAR= option in the COSAN statement as you do in the VAR= option in the RAM statement. Then, you specify the formula for the covariance structures for the set of variables in the VAR= list. Because the covariance structure formula is symmetric, you only need to specify "half" of it. That is, the specification J(9,IDE)*A(9,GEN,IMI)*P(9,SYM) in the COSAN statement automatically expands to
| |
 |
|
|
which is the required covariance structures. The arguments in the matrices represent the number of columns, the matrix type, and the transformation type (optional), respectively. For example, the notation A(9, GEN, IMI) means that matrix  has nine columns and it is a general (GEN) rectangular or square matrix. You do not specify the number of rows for matrix
has nine columns and it is a general (GEN) rectangular or square matrix. You do not specify the number of rows for matrix  explicitly, but PROC CALIS can deduce that because matrix
explicitly, but PROC CALIS can deduce that because matrix  follows matrix
follows matrix  in the multiplication. To make matrix multiplication conformable, the number of rows for matrix
in the multiplication. To make matrix multiplication conformable, the number of rows for matrix  must be the same as the number of columns for matrix
must be the same as the number of columns for matrix  , which is nine. The IMI notation means the identity-minus-inverse transformation, which results in putting
, which is nine. The IMI notation means the identity-minus-inverse transformation, which results in putting  in the expression. Matrix
in the expression. Matrix  in the covariance structure formula is a 9
in the covariance structure formula is a 9  9 symmetric matrix. It does not have any transformation in the formula. Matrix
9 symmetric matrix. It does not have any transformation in the formula. Matrix  in the covariance structure formula is a so-called generalized identity matrix (IDE), which has six rows and nine columns. Basically, you use this matrix to select the observed variables in the covariance structure formula. The exact form of this matrix will become clear when the PROC CALIS output is shown.
in the covariance structure formula is a so-called generalized identity matrix (IDE), which has six rows and nine columns. Basically, you use this matrix to select the observed variables in the covariance structure formula. The exact form of this matrix will become clear when the PROC CALIS output is shown.
Next, you use two MATRIX statements to specify the parameters in the model matrices  and
and  , for RAM model matrices _A_ and _P_, respectively. For example, in the first entry of the MATRIX statement for the
, for RAM model matrices _A_ and _P_, respectively. For example, in the first entry of the MATRIX statement for the  matrix, you specify the elements [1,7], [2,7], and [8,7] by 1.0, 0.833, and beta, respectively. The first two elements are fixed constants, while the last one is a free parameter named beta. Similarly, you specify all the fixed or free parameters in matrix
matrix, you specify the elements [1,7], [2,7], and [8,7] by 1.0, 0.833, and beta, respectively. The first two elements are fixed constants, while the last one is a free parameter named beta. Similarly, you specify all the fixed or free parameters in matrix  , which reflects the same pattern you specify for the _A_ matrix of the RAM model, as shown in Output 25.26.1.
, which reflects the same pattern you specify for the _A_ matrix of the RAM model, as shown in Output 25.26.1.
For the  matrix, you specify the parameters in the same fashion. Because
matrix, you specify the parameters in the same fashion. Because  is defined as a symmetric matrix, you need to specify only the lower triangular elements. In the first entry of the MATRIX statement for the
is defined as a symmetric matrix, you need to specify only the lower triangular elements. In the first entry of the MATRIX statement for the  matrix, you specify the [1,1] element, but the trailing parameter list has six parameters. The [1,1] notation here is interpreted as the starting location of the matrix. It proceeds to [2,2], [3,3], [4,4] and so on. The length of the trailing parameter list determines the number of elements being specified. Therefore, the last parameter in this entry is for
matrix, you specify the [1,1] element, but the trailing parameter list has six parameters. The [1,1] notation here is interpreted as the starting location of the matrix. It proceeds to [2,2], [3,3], [4,4] and so on. The length of the trailing parameter list determines the number of elements being specified. Therefore, the last parameter in this entry is for  , which is a free parameter theta4. Similarly, you define all other parameters in the
, which is a free parameter theta4. Similarly, you define all other parameters in the  matrix, which reflects the same pattern you specify for the _P_ matrix of the RAM model, as shown in Output 25.26.2.
matrix, which reflects the same pattern you specify for the _P_ matrix of the RAM model, as shown in Output 25.26.2.
In the VNAMES statement, you can specify the column variable names for the model matrices. You provide a set of nine variable names for the column of matrix  in the pairs of brackets. The first six names are those of the observed variables in the COSAN model, while the last six names are for latent factors. How about the row variable names for matrix
in the pairs of brackets. The first six names are those of the observed variables in the COSAN model, while the last six names are for latent factors. How about the row variable names for matrix  ? Because matrix
? Because matrix  is the first matrix in the covariance structure formula, its row names are automatically the same as the names of the observed variables in the VAR= list of the COSAN statement. Next, you specify the column variable names of matrix
is the first matrix in the covariance structure formula, its row names are automatically the same as the names of the observed variables in the VAR= list of the COSAN statement. Next, you specify the column variable names of matrix  . You equate that to matrix
. You equate that to matrix  , meaning that the column variable names in matrix
, meaning that the column variable names in matrix  are the same those for matrix
are the same those for matrix  . How about the row variable names for matrix
. How about the row variable names for matrix  ? Because matrix
? Because matrix  follows matrix
follows matrix  in the covariance structure formula, its row names are automatically same as the column names for matrix
in the covariance structure formula, its row names are automatically same as the column names for matrix  . Lastly, you define that the column names for matrix
. Lastly, you define that the column names for matrix  are the same as those for matrix
are the same as those for matrix  .
.
Notice that column names serve only as labels. PROC CALIS does not know the identities of the row and column variables. For example, the first column of matrix  is Anomie67, which is also a name for an observed variable in the COSAN model. Keeping other specifications intact, you could name this column by any other name without affecting the model estimation. It is recommended that you use sensible names that help you remember the identities of the row and column variables, such as this example shows.
is Anomie67, which is also a name for an observed variable in the COSAN model. Keeping other specifications intact, you could name this column by any other name without affecting the model estimation. It is recommended that you use sensible names that help you remember the identities of the row and column variables, such as this example shows.
Output 25.26.3 shows the modeling information and the observed variables in the COSAN model. PROC CALIS analyzed the covariance structures of the six observed variables listed in Output 25.26.3.
Output 25.26.3
Modeling Information of the COSAN Model for the Wheaton Data: RAM Emulation
| WORK.WHEATON |
| 932 |
| COSAN |
| Covariances |
| Anomie67 Powerless67 Anomie71 Powerless71 Education SEI |
Output 25.26.4 shows the covariance structures and some properties of the model matrices. The covariance structure formula for Sigma is defined as required. You can also check the matrix properties in this output to see if they are what you intend them to be.
Output 25.26.4
The Covariance Structures and Model Matrices of the COSAN Model for the Wheaton Data: RAM Emulation
| Sigma = |
J*inv(_I_-A)*P*(inv(_I_-A))`*J` |
| A |
9 |
9 |
GEN: Square |
| J |
6 |
9 |
IDE: (I || 0) |
| P |
9 |
9 |
SYM: Symmetric |
Output 25.26.4 shows that  is a 6
is a 6  9 "identity" matrix
9 "identity" matrix  . Essentially,
. Essentially,  is a selection matrix that contains either 0 or 1 as its elements. The role of matrix
is a selection matrix that contains either 0 or 1 as its elements. The role of matrix  in the covariance structure formula is to extract first six rows and columns in the inner covariance structures
in the covariance structure formula is to extract first six rows and columns in the inner covariance structures  (which is 9
(which is 9  9) to form the covariance structures only for the observed variables (which is 6
9) to form the covariance structures only for the observed variables (which is 6  6). But how can this identity matrix have more columns (9) than rows (6)? In common mathematical notation, an identity matrix must always be a square matrix. However, for convenience in notation, PROC CALIS generalizes it to the IDE type. An IDE matrix that has the same numbers of columns and rows is a square identity matrix. If an IDE matrix has more columns than rows, it denotes an identity matrix concatenated (to the right) by a null matrix (that is, the
6). But how can this identity matrix have more columns (9) than rows (6)? In common mathematical notation, an identity matrix must always be a square matrix. However, for convenience in notation, PROC CALIS generalizes it to the IDE type. An IDE matrix that has the same numbers of columns and rows is a square identity matrix. If an IDE matrix has more columns than rows, it denotes an identity matrix concatenated (to the right) by a null matrix (that is, the  notation). If an IDE matrix has more rows than columns, it denotes an identity matrix appended (to the bottom) by a null matrix (that is, the
notation). If an IDE matrix has more rows than columns, it denotes an identity matrix appended (to the bottom) by a null matrix (that is, the  notation). The generalized definition for the IDE matrix offers an efficient way to define selection matrix, such as the
notation). The generalized definition for the IDE matrix offers an efficient way to define selection matrix, such as the  matrix shown in this example.
matrix shown in this example.
Output 25.26.5 shows the model fit chi-square of the COSAN model. This is the same model fit as in Output 25.15.6 of Example 25.15, as expected.
Output 25.26.5
Model Fit of the COSAN Model for the Wheaton Data: RAM Emulation
Output 25.26.6 shows the estimates in the  matrix.
matrix.
Output 25.26.6
Estimate of the  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
The estimates in Output 25.26.6 from the COSAN model specification are essentially the same as those from the RAM model specification, as shown in the matrix form in Output 25.26.7.
Output 25.26.7
Estimate of the  Matrix by the RAM Model Specification
Matrix by the RAM Model Specification
Output 25.26.8 shows the estimates in the  matrix.
matrix.
Output 25.26.8
Estimate of the  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
Again, aside from very minor numerical differences, the estimates shown in Output 25.26.8 from the COSAN model specification are essentially the same as those from the RAM model specification, as shown in the matrix form in Output 25.26.9.
Output 25.26.9
Estimate of the  Matrix by the RAM Model Specification
Matrix by the RAM Model Specification
Emulating the EQS model by the COSAN Modeling Language
The LINEQS modeling language in PROC CALIS enables you to specify the functional relationships among variables by using the equation input, much the same way that you can do with the EQS software (Bentler; 1995). The covariance structure formula for the observed variables in the EQS model is
where  is an identity matrix,
is an identity matrix,  is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables,
is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables,  is a square matrix for specifying relationships among the endogenous variables, Gamma is a matrix for specifying relationships between the endogenous variables and the exogenous variables, and
is a square matrix for specifying relationships among the endogenous variables, Gamma is a matrix for specifying relationships between the endogenous variables and the exogenous variables, and  is a matrix for specifying the variances and covariances of the exogenous variables. Notice that in the EQS model, error or disturbance variables are counted as exogenous variables in the model.
is a matrix for specifying the variances and covariances of the exogenous variables. Notice that in the EQS model, error or disturbance variables are counted as exogenous variables in the model.
In Example 25.20, you use the following LINEQS specification for the Wheaton data:
proc calis nobs=932 data=Wheaton primat nose;
lineqs
Anomie67 = 1.0 * f_Alien67 + e1,
Powerless67 = 0.833 * f_Alien67 + e2,
Anomie71 = 1.0 * f_Alien71 + e3,
Powerless71 = 0.833 * f_Alien71 + e4,
Education = 1.0 * f_SES + e5,
SEI = lambda * f_SES + e6,
f_Alien67 = gamma1 * f_SES + d1,
f_Alien71 = gamma2 * f_SES + beta * f_Alien67 + d2;
variance
E1 = theta1,
E2 = theta2,
E3 = theta1,
E4 = theta2,
E5 = theta3,
E6 = theta4,
D1 = psi1,
D2 = psi2,
f_SES = phi;
cov
E1 E3 = theta5,
E2 E4 = theta5;
run;
In the LINEQS statement, you specify all the functional relationships among variables. In the VARIANCE and COV statements, you specify all the variance and covariance parameters in the model. None of the parameters is specified as a matrix element in the LINEQS model. The default output by PROC CALIS does not print the EQS model matrices. To print these model matrices, you use the PRIMAT option in the PROC CALIS statement. Output 25.26.10, Output 25.26.11, and Output 25.26.12 show the initial specification of these model matrices:
Output 25.26.10
The Initial _EQSBETA_ Matrix by the LINEQS Model Specification
Output 25.26.11
The Initial _EQSGAMMA_ Matrix by the LINEQS Model Specification
Output 25.26.12
The Initial _EQSPHI_ Matrix by the LINEQS Model Specification
In the COSAN modeling language, you need to provide the three initial model matrices and the covariance structure formula for 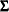 , which is shown in the following statements:
, which is shown in the following statements:
proc calis cov data=Wheaton nobs=932 nose;
cosan
var = Anomie67 Anomie71 Education Powerless67 Powerless71 SEI,
J(8, IDE) * Beta(8, GEN, IMI) * Gamma(9, GEN) * Phi(9, SYM);
matrix Beta
[1 4 8 , 7] = 1.0 0.833 beta,
[2 5 , 8] = 1.0 0.833 ;
matrix Gamma
[3 6 7 8 , 1] = 1.0 lambda gamma1 gamma2,
[1,2] = 8 * 1.0;
matrix Phi
[1,1] = phi 2*theta1 theta3 2*theta2 theta4 psi1 psi2,
[3,2] = theta5 ,
[6,5] = theta5 ;
vnames J = [Anomie67 Anomie71 Education Powerless67 Powerless71 SEI
f_Alien67 f_Alien71],
Beta = J,
Gamma = [f_SES e1 e3 e5 e2 e4 e6 d1 d2],
Phi = Gamma;
run;
In the PROC CALIS statement, you provide the data set in the DATA= option and the number of observations in the NOBS= option. You use the NOSE option to turn off the computation of the standard error estimates.
In the VAR= option of the COSAN statement, you provide the list of observed variables for the analysis. You arrange the observed variables in such a way that they are in the same order as in Output 25.26.10, Output 25.26.10, and Output 25.26.12. This is useful for comparing the results from the LINEQS and COSAN model specifications. After the specification of the observed variables, you specify the covariance structure model in the COSAN statement. Again, you only need to specify "half" of it. That is, the specification J(8,IDE)*Beta(8,GEN,IMI)*Gamma(9,GEN)*Phi(9,SYM) in the COSAN statement automatically expands to
which is the required covariance structures. Matrix properties and transformation types are defined in the arguments for the matrices.
Next, you use three matrix statements to specify the parameters in the matrix elements. The specifications here reflect exactly the initial specifications for the LINEQS model matrices as shown in Output 25.26.10, Output 25.26.10, and Output 25.26.12.
In the VNAMES statement, you specify the column variable names for the matrices. The column variable names of the  matrix include all the observed variable names and the names of the intended endogenous latent factors f_Alien67 and f_Alien71. The column variable names for the
matrix include all the observed variable names and the names of the intended endogenous latent factors f_Alien67 and f_Alien71. The column variable names for the  matrix are the same as those for matrix
matrix are the same as those for matrix  . The column variables for the
. The column variables for the  matrix include the intended latent factor f_SES and error variable names e1–e6 and d1–d2, which are arranged in such a way that they match the order of the error variables in the LINEQS output shown in Output 25.26.12.
matrix include the intended latent factor f_SES and error variable names e1–e6 and d1–d2, which are arranged in such a way that they match the order of the error variables in the LINEQS output shown in Output 25.26.12.
Output 25.26.13 shows the covariance structures and some properties of the model matrices. The covariance structure formula for  is defined as required. You can also check the matrix properties in this output to see if they are what you intend them to be.
is defined as required. You can also check the matrix properties in this output to see if they are what you intend them to be.
Output 25.26.13
The Covariance Structures and Model Matrices of the COSAN Model for the Wheaton Data: EQS Emulation
| Sigma = |
J*inv(_I_-Beta)*Gamma*Phi*Gamma`*(inv(_I_-Beta))`*J` |
| Beta |
8 |
8 |
GEN: Square |
| Gamma |
8 |
9 |
GEN: Rectangular |
| J |
6 |
8 |
IDE: (I || 0) |
| Phi |
9 |
9 |
SYM: Symmetric |
Output 25.26.14 shows the model fit chi-square of the current COSAN model. As expected, this is the same model fit as in Output 25.15.6 of Example 25.15 and in Output 25.26.5.
Output 25.26.14
Model Fit of the COSAN Model for the Wheaton Data: EQS Emulation
Output 25.26.15 shows the estimates of the  matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSBETA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.16.
matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSBETA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.16.
Output 25.26.15
Estimate of the  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
Output 25.26.16
Estimate of the _EQSBETA_ Matrix by the LINEQS Model Specification
Output 25.26.17 shows the estimates of the  matrix by the COSAN model specification. Again, these estimates are essentially the same as the estimates of the _EQSGAMMA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.18.
matrix by the COSAN model specification. Again, these estimates are essentially the same as the estimates of the _EQSGAMMA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.18.
Output 25.26.17
Estimate of the Gamma Matrix by the COSAN Model Specification
Output 25.26.18
Estimate of the _EQSGAMMA_ Matrix by the LINEQS Model Specification
Finally, Output 25.26.19 shows the estimates of the  matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSPHI_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.20.
matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSPHI_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.20.
Output 25.26.19
Estimate of the  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
Output 25.26.20
Estimate of the _EQSPHI_ Matrix by the LINEQS Model Specification
 (_A_) matrix. You specify all the information regarding the variances and covariances (that is, the double-headed arrows in the path diagram) in the
(_A_) matrix. You specify all the information regarding the variances and covariances (that is, the double-headed arrows in the path diagram) in the  (_P_) matrix. See the section The RAM Model for more details about the mathematical model for RAM. Once you define these two matrices, the implied covariance structures for the observed variables are derived by the formula
(_P_) matrix. See the section The RAM Model for more details about the mathematical model for RAM. Once you define these two matrices, the implied covariance structures for the observed variables are derived by the formula 
 is an identity matrix and
is an identity matrix and  is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables.
is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables. 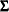 .
. 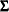 in the COSAN model specification, which is shown in the following statements:
in the COSAN model specification, which is shown in the following statements: 
 has nine columns and it is a general (GEN) rectangular or square matrix. You do not specify the number of rows for matrix
has nine columns and it is a general (GEN) rectangular or square matrix. You do not specify the number of rows for matrix  explicitly, but PROC CALIS can deduce that because matrix
explicitly, but PROC CALIS can deduce that because matrix  follows matrix
follows matrix  in the multiplication. To make matrix multiplication conformable, the number of rows for matrix
in the multiplication. To make matrix multiplication conformable, the number of rows for matrix  must be the same as the number of columns for matrix
must be the same as the number of columns for matrix  , which is nine. The IMI notation means the identity-minus-inverse transformation, which results in putting
, which is nine. The IMI notation means the identity-minus-inverse transformation, which results in putting  in the expression. Matrix
in the expression. Matrix  in the covariance structure formula is a 9
in the covariance structure formula is a 9  9 symmetric matrix. It does not have any transformation in the formula. Matrix
9 symmetric matrix. It does not have any transformation in the formula. Matrix  in the covariance structure formula is a so-called generalized identity matrix (IDE), which has six rows and nine columns. Basically, you use this matrix to select the observed variables in the covariance structure formula. The exact form of this matrix will become clear when the PROC CALIS output is shown.
in the covariance structure formula is a so-called generalized identity matrix (IDE), which has six rows and nine columns. Basically, you use this matrix to select the observed variables in the covariance structure formula. The exact form of this matrix will become clear when the PROC CALIS output is shown.  and
and  , for RAM model matrices _A_ and _P_, respectively. For example, in the first entry of the MATRIX statement for the
, for RAM model matrices _A_ and _P_, respectively. For example, in the first entry of the MATRIX statement for the  matrix, you specify the elements [1,7], [2,7], and [8,7] by 1.0, 0.833, and beta, respectively. The first two elements are fixed constants, while the last one is a free parameter named beta. Similarly, you specify all the fixed or free parameters in matrix
matrix, you specify the elements [1,7], [2,7], and [8,7] by 1.0, 0.833, and beta, respectively. The first two elements are fixed constants, while the last one is a free parameter named beta. Similarly, you specify all the fixed or free parameters in matrix  , which reflects the same pattern you specify for the _A_ matrix of the RAM model, as shown in Output 25.26.1.
, which reflects the same pattern you specify for the _A_ matrix of the RAM model, as shown in Output 25.26.1.  matrix, you specify the parameters in the same fashion. Because
matrix, you specify the parameters in the same fashion. Because  is defined as a symmetric matrix, you need to specify only the lower triangular elements. In the first entry of the MATRIX statement for the
is defined as a symmetric matrix, you need to specify only the lower triangular elements. In the first entry of the MATRIX statement for the  matrix, you specify the [1,1] element, but the trailing parameter list has six parameters. The [1,1] notation here is interpreted as the starting location of the matrix. It proceeds to [2,2], [3,3], [4,4] and so on. The length of the trailing parameter list determines the number of elements being specified. Therefore, the last parameter in this entry is for
matrix, you specify the [1,1] element, but the trailing parameter list has six parameters. The [1,1] notation here is interpreted as the starting location of the matrix. It proceeds to [2,2], [3,3], [4,4] and so on. The length of the trailing parameter list determines the number of elements being specified. Therefore, the last parameter in this entry is for  , which is a free parameter theta4. Similarly, you define all other parameters in the
, which is a free parameter theta4. Similarly, you define all other parameters in the  matrix, which reflects the same pattern you specify for the _P_ matrix of the RAM model, as shown in Output 25.26.2.
matrix, which reflects the same pattern you specify for the _P_ matrix of the RAM model, as shown in Output 25.26.2.  in the pairs of brackets. The first six names are those of the observed variables in the COSAN model, while the last six names are for latent factors. How about the row variable names for matrix
in the pairs of brackets. The first six names are those of the observed variables in the COSAN model, while the last six names are for latent factors. How about the row variable names for matrix  ? Because matrix
? Because matrix  is the first matrix in the covariance structure formula, its row names are automatically the same as the names of the observed variables in the VAR= list of the COSAN statement. Next, you specify the column variable names of matrix
is the first matrix in the covariance structure formula, its row names are automatically the same as the names of the observed variables in the VAR= list of the COSAN statement. Next, you specify the column variable names of matrix  . You equate that to matrix
. You equate that to matrix  , meaning that the column variable names in matrix
, meaning that the column variable names in matrix  are the same those for matrix
are the same those for matrix  . How about the row variable names for matrix
. How about the row variable names for matrix  ? Because matrix
? Because matrix  follows matrix
follows matrix  in the covariance structure formula, its row names are automatically same as the column names for matrix
in the covariance structure formula, its row names are automatically same as the column names for matrix  . Lastly, you define that the column names for matrix
. Lastly, you define that the column names for matrix  are the same as those for matrix
are the same as those for matrix  .
.  is Anomie67, which is also a name for an observed variable in the COSAN model. Keeping other specifications intact, you could name this column by any other name without affecting the model estimation. It is recommended that you use sensible names that help you remember the identities of the row and column variables, such as this example shows.
is Anomie67, which is also a name for an observed variable in the COSAN model. Keeping other specifications intact, you could name this column by any other name without affecting the model estimation. It is recommended that you use sensible names that help you remember the identities of the row and column variables, such as this example shows.  is a 6
is a 6  9 "identity" matrix
9 "identity" matrix  . Essentially,
. Essentially,  is a selection matrix that contains either 0 or 1 as its elements. The role of matrix
is a selection matrix that contains either 0 or 1 as its elements. The role of matrix  in the covariance structure formula is to extract first six rows and columns in the inner covariance structures
in the covariance structure formula is to extract first six rows and columns in the inner covariance structures  (which is 9
(which is 9  9) to form the covariance structures only for the observed variables (which is 6
9) to form the covariance structures only for the observed variables (which is 6  6). But how can this identity matrix have more columns (9) than rows (6)? In common mathematical notation, an identity matrix must always be a square matrix. However, for convenience in notation, PROC CALIS generalizes it to the IDE type. An IDE matrix that has the same numbers of columns and rows is a square identity matrix. If an IDE matrix has more columns than rows, it denotes an identity matrix concatenated (to the right) by a null matrix (that is, the
6). But how can this identity matrix have more columns (9) than rows (6)? In common mathematical notation, an identity matrix must always be a square matrix. However, for convenience in notation, PROC CALIS generalizes it to the IDE type. An IDE matrix that has the same numbers of columns and rows is a square identity matrix. If an IDE matrix has more columns than rows, it denotes an identity matrix concatenated (to the right) by a null matrix (that is, the  notation). If an IDE matrix has more rows than columns, it denotes an identity matrix appended (to the bottom) by a null matrix (that is, the
notation). If an IDE matrix has more rows than columns, it denotes an identity matrix appended (to the bottom) by a null matrix (that is, the  notation). The generalized definition for the IDE matrix offers an efficient way to define selection matrix, such as the
notation). The generalized definition for the IDE matrix offers an efficient way to define selection matrix, such as the  matrix shown in this example.
matrix shown in this example.  matrix.
matrix.  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
 Matrix by the RAM Model Specification
Matrix by the RAM Model Specification
 matrix.
matrix.  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
 Matrix by the RAM Model Specification
Matrix by the RAM Model Specification

 is an identity matrix,
is an identity matrix,  is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables,
is a selection matrix that contains 0 or 1 as its elements for selecting the covariance structures elements for the observed variables,  is a square matrix for specifying relationships among the endogenous variables, Gamma is a matrix for specifying relationships between the endogenous variables and the exogenous variables, and
is a square matrix for specifying relationships among the endogenous variables, Gamma is a matrix for specifying relationships between the endogenous variables and the exogenous variables, and  is a matrix for specifying the variances and covariances of the exogenous variables. Notice that in the EQS model, error or disturbance variables are counted as exogenous variables in the model.
is a matrix for specifying the variances and covariances of the exogenous variables. Notice that in the EQS model, error or disturbance variables are counted as exogenous variables in the model. 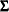 , which is shown in the following statements:
, which is shown in the following statements: 
 matrix include all the observed variable names and the names of the intended endogenous latent factors f_Alien67 and f_Alien71. The column variable names for the
matrix include all the observed variable names and the names of the intended endogenous latent factors f_Alien67 and f_Alien71. The column variable names for the  matrix are the same as those for matrix
matrix are the same as those for matrix  . The column variables for the
. The column variables for the  matrix include the intended latent factor f_SES and error variable names e1–e6 and d1–d2, which are arranged in such a way that they match the order of the error variables in the LINEQS output shown in Output 25.26.12.
matrix include the intended latent factor f_SES and error variable names e1–e6 and d1–d2, which are arranged in such a way that they match the order of the error variables in the LINEQS output shown in Output 25.26.12.  is defined as required. You can also check the matrix properties in this output to see if they are what you intend them to be.
is defined as required. You can also check the matrix properties in this output to see if they are what you intend them to be.  matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSBETA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.16.
matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSBETA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.16.  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification
 matrix by the COSAN model specification. Again, these estimates are essentially the same as the estimates of the _EQSGAMMA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.18.
matrix by the COSAN model specification. Again, these estimates are essentially the same as the estimates of the _EQSGAMMA_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.18.  matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSPHI_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.20.
matrix by the COSAN model specification. These estimates are essentially the same as the estimates of the _EQSPHI_ matrix obtained from the LINEQS model specification, as shown in Output 25.26.20.  Matrix by the COSAN Model Specification
Matrix by the COSAN Model Specification