| The VARIOGRAM Procedure |
Example 95.1 Theoretical Semivariogram Model Fitting
This example continues the introduction study presented in the section Getting Started: VARIOGRAM Procedure by fitting a theoretical semivariogram model to the estimated classical sample semivariogram in Figure 95.8. You will use PROC NLIN to perform the model fit and to compare two different approaches: the ordinary least squares (OLS) and the weighted least squares (WLS) fitting methods.
A review of the coal seam thickness empirical semivariogram in Figure 95.8 shows first a slow, then rapid rise from the origin, suggesting a Gaussian-type form:
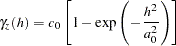 |
as shown in the section Theoretical Semivariogram Models.
By experimentation, you find that a sill of 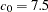 and a range of
and a range of 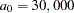 feet (effective range
feet (effective range 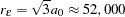 feet) provide a reasonable fit of the preceding semivariogram model. You can use these values as initial guesses in the least squares fitting process. For the fitting you need the output data set that is produced by the parameters used in the section Theoretical Semivariogram Models. The following statements skip the autocorrelation statistics and the creation of plots, and produce the required output data for the semivariogram table. Note that for the fitting process you need information about the semivariance variance, which you obtain by specifying the CL option in the COMPUTE statement.
feet) provide a reasonable fit of the preceding semivariogram model. You can use these values as initial guesses in the least squares fitting process. For the fitting you need the output data set that is produced by the parameters used in the section Theoretical Semivariogram Models. The following statements skip the autocorrelation statistics and the creation of plots, and produce the required output data for the semivariogram table. Note that for the fitting process you need information about the semivariance variance, which you obtain by specifying the CL option in the COMPUTE statement.
title 'Theoretical Semivariogram Model Fitting Example'; ods graphics on;
proc variogram data=thick outv=outv plots=none;
compute lagd=7 maxlag=10 robust cl;
coordinates xc=East yc=North;
ods output SemivariogramTable=sv;
var Thick;
run;
Since MAXLAG=10, you computed the empirical semivariogram at 11 points (see also Figure 95.8). You would like to obtain a smooth theoretical semivariogram plot, so you need to estimate the theoretical model at more points on the horizontal (distance) axis. The following statements create a sequence of such distance points from 0 to 70,000 feet and space them 500 feet apart:
data pv;
do Distance = 0 to 70 by 0.5;
Semivariance = .;
output;
end;
run;
data sv; set sv pv; by Distance; run;
PROC NLIN performs its own analysis based on the Gaussian model you provided as input. By invoking the NLIN procedure twice, as shown in the following statements, you obtain the estimates for the theoretical model parameters for the OLS and WLS fitting methods. Notice in the WLS case that the weights are defined as the inverse of the computed semivariance variance.
proc nlin data=sv;
parms Range=30
Sill=7.5;
model Semivariance =
Sill*(1-exp(-Distance*Distance/(Range*Range)));
output out=OLS p=OLS;
run;
proc nlin data=sv;
parms Range=30
Sill=7.5;
model Semivariance =
Sill*(1-exp(-Distance*Distance/(Range*Range)));
_weight_ = 1/SemivarianceStdErr/SemivarianceStdErr;
output out=WLS p=WLS;
run;
Output 95.1.1 shows part of the NLIN procedure output that displays the model parameters statistics for the OLS methods.
| Parameter | Estimate | Approx Std Error |
Approximate 95% Confidence Limits |
|
|---|---|---|---|---|
| Range | 27.1706 | 1.9211 | 22.8247 | 31.5165 |
| Sill | 7.1628 | 0.2781 | 6.5337 | 7.7919 |
The corresponding PROC NLIN output for the WLS method is displayed in the following Output 95.1.2.
| Parameter | Estimate | Approx Std Error |
Approximate 95% Confidence Limits |
|
|---|---|---|---|---|
| Range | 30.6239 | 1.7382 | 26.6917 | 34.5560 |
| Sill | 7.2881 | 0.4082 | 6.3646 | 8.2116 |
Finally, you visualize the outcome of the fitting analysis. You start with a DATA step to arrange the WLS and OLS data in the same data set. Then you use the SGPLOT procedure to produce a plot showing the empirical and fitted theoretical semivariograms. This sequence is exhibited in the following statements:
data pv;
merge WLS OLS;
run;
proc sgplot data=pv;
title "Empirical and Fitted Theoretical Semivariogram";
xaxis label = "Distance" grid;
yaxis label = "Semivariance" grid;
scatter y=Semivariance x=Distance /
markerattrs = GraphData1(symbol=circle)
name = 'SemiVarClassical'
yerrorupper = UpperCLSemivariance
yerrorlower = LowerCLSemivariance;
scatter y=RobustSemivariance x=Distance /
markerattrs = GraphData2(symbol=X)
name = 'SemiVarRobust';
series x=Distance y=WLS /
lineattrs = (thickness=2px color=blue)
name = 'SemivarPredWgh';
series x=Distance y=OLS /
lineattrs = (thickness=2px color=black
pattern=MediumDash)
name = 'SemivarPredUnw';
discretelegend 'SemiVarClassical' 'SemiVarRobust'
'SemivarPredWgh' 'SemivarPredUnw';
run;
ods graphics off;
Output 95.1.3 demonstrates the difference between the ordinary and weighted least squares fitting results: WLS achieves a more accurate fit closer to the empirical points with the smaller variances, because the weights are expressed as the inverse of these variances. In the presence of a sizable population per distance class, you expect the points with lower variance to be situated close to the origin, as the semivariance variance expression suggests in the section Theoretical and Computational Details of the Semivariogram. Hence, you expect in general the WLS method to perform with increased accuracy at short distances because it acknowledges the smaller variance at small  . In contrast, the OLS approach performs a least squares overall best fit as it assumes constant variance.
. In contrast, the OLS approach performs a least squares overall best fit as it assumes constant variance.
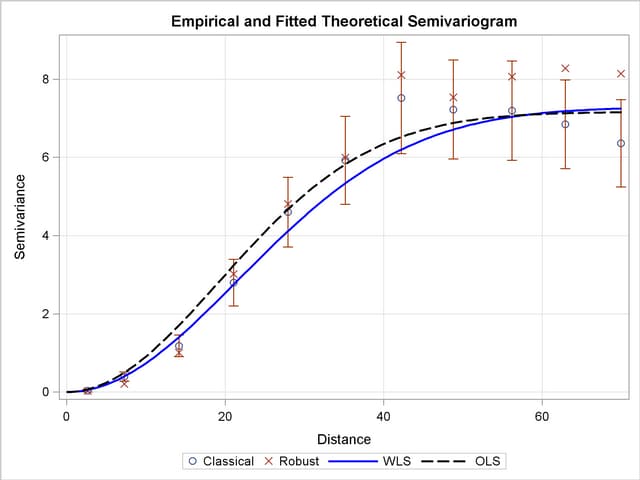
The WLS method is preferred over the OLS method because it is important to obtain accurate estimates of the spatial continuity closer to the origin  . Another advantage of WLS over OLS is that OLS falsely assumes that the differences in the optimization process are normally distributed and independent. However, WLS has the disadvantage that the weights depend on the fitting parameters.
. Another advantage of WLS over OLS is that OLS falsely assumes that the differences in the optimization process are normally distributed and independent. However, WLS has the disadvantage that the weights depend on the fitting parameters.
Other fitting methods include maximum likelihood approaches that rely crucially on the normality assumption for the data distribution, and the generalized least squares method, which offers better accuracy but is computationally more demanding. You can find extensive discussions of these issues in Cressie (1993, Section 2.3), Jian, Olea, and Yu (1996), Stein (1988), and Schabenberger and Gotway (2005).
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.