| The CALIS Procedure |
Example 25.2 Simultaneous Equations with Intercept
The demand-and-supply food example of Kmenta (1971, pp. 565, 582) is used to illustrate the use of PROC CALIS for the estimation of intercepts and coefficients of simultaneous equations. The model is specified by two simultaneous equations containing two endogenous variables 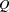 and
and  and three exogenous variables
and three exogenous variables 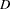 ,
, 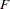 , and
, and  ,
,
 |
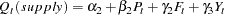 |
for 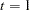 , ...,
, ..., 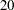 .
.
The LINEQS statement requires that each endogenous variable appear on the left-hand side of exactly one equation. Instead of analyzing the system
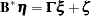 |
PROC CALIS analyzes the equivalent system
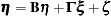 |
with  . This requires that one of the preceding equations be solved for
. This requires that one of the preceding equations be solved for 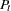 . Solving the second equation for
. Solving the second equation for 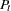 yields
yields
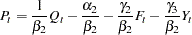 |
You can estimate the intercepts of a system of simultaneous equations by applying PROC CALIS to the uncorrected covariance (UCOV) matrix of the data set that is augmented by an additional constant variable with the value 1. In the following statements, the uncorrected covariance matrix is augmented by an additional variable INTERCEPT by using the AUGMENT option. The PROC CALIS statement contains the options UCOV and AUG to compute and analyze an augmented UCOV matrix from the input data set FOOD.
data food;
title 'Food example of KMENTA(1971, p.565 & 582)';
input Q P D F Y;
label Q='Food Consumption per Head'
P='Ratio of Food Prices to General Price'
D='Disposable Income in Constant Prices'
F='Ratio of Preceding Years Prices'
Y='Time in Years 1922-1941';
datalines;
98.485 100.323 87.4 98.0 1
99.187 104.264 97.6 99.1 2
102.163 103.435 96.7 99.1 3
101.504 104.506 98.2 98.1 4
104.240 98.001 99.8 110.8 5
103.243 99.456 100.5 108.2 6
103.993 101.066 103.2 105.6 7
99.900 104.763 107.8 109.8 8
100.350 96.446 96.6 108.7 9
102.820 91.228 88.9 100.6 10
95.435 93.085 75.1 81.0 11
92.424 98.801 76.9 68.6 12
94.535 102.908 84.6 70.9 13
98.757 98.756 90.6 81.4 14
105.797 95.119 103.1 102.3 15
100.225 98.451 105.1 105.0 16
103.522 86.498 96.4 110.5 17
99.929 104.016 104.4 92.5 18
105.223 105.769 110.7 89.3 19
106.232 113.490 127.1 93.0 20
;
proc calis ucov aug data=food pshort;
lineqs
Q = alf1 Intercept + alf2 P + alf3 D + E1,
P = gam1 Intercept + gam2 Q + gam3 F + gam4 Y + E2;
std
E1-E2 = eps1-eps2;
cov
E1-E2 = eps3;
bounds
eps1-eps2 >= 0. ;
run;
The following statements, an essentially equivalent model specification, use program code to reparameterize the model in terms of the original equations; the output is displayed in Output 25.2.1.
proc calis data=food ucov aug pshort;
lineqs
Q = alphal Intercept + beta1 P + gamma1 D + E1,
P = alpha2_b Intercept + gamma2_b F + gamma3_b Y + _b Q + E2;
std
E1-E2 = eps1-eps2;
cov
E1-E2 = eps3;
parameters alpha2 (50.) beta2 gamma2 gamma3 (3*.25);
alpha2_b = -alpha2 / beta2;
gamma2_b = -gamma2 / beta2;
gamma3_b = -gamma3 / beta2;
_b = 1 / beta2;
bounds
eps1-eps2 >= 0. ;
run;
| Parameter Estimates | 10 |
|---|---|
| Functions (Observations) | 21 |
| Lower Bounds | 2 |
| Upper Bounds | 0 |
| Optimization Start | |||
|---|---|---|---|
| Active Constraints | 0 | Objective Function | 2.3500065042 |
| Max Abs Gradient Element | 203.9741437 | Radius | 62167.829174 |
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 0 | 1.19094 | 1.1591 | 3.9410 | 0 | 0.688 | ||
| 2 | 0 | 5 | 0 | 0.32678 | 0.8642 | 9.9864 | 0.00127 | 2.356 | ||
| 3 | 0 | 7 | 0 | 0.19108 | 0.1357 | 5.5100 | 0.00006 | 0.685 | ||
| 4 | 0 | 10 | 0 | 0.16682 | 0.0243 | 2.0513 | 0.00005 | 0.867 | ||
| 5 | 0 | 12 | 0 | 0.16288 | 0.00393 | 1.0570 | 0.00014 | 0.828 | ||
| 6 | 0 | 13 | 0 | 0.16132 | 0.00156 | 0.3643 | 0.00004 | 0.864 | ||
| 7 | 0 | 15 | 0 | 0.16077 | 0.000557 | 0.2176 | 0.00006 | 0.984 | ||
| 8 | 0 | 16 | 0 | 0.16052 | 0.000250 | 0.1819 | 0.00001 | 0.618 | ||
| 9 | 0 | 17 | 0 | 0.16032 | 0.000201 | 0.0662 | 0 | 0.971 | ||
| 10 | 0 | 18 | 0 | 0.16030 | 0.000011 | 0.0195 | 0 | 1.108 | ||
| 11 | 0 | 19 | 0 | 0.16030 | 6.116E-7 | 0.00763 | 0 | 1.389 | ||
| 12 | 0 | 20 | 0 | 0.16030 | 9.454E-8 | 0.00301 | 0 | 1.389 | ||
| 13 | 0 | 21 | 0 | 0.16030 | 1.461E-8 | 0.00118 | 0 | 1.388 | ||
| 14 | 0 | 22 | 0 | 0.16030 | 2.269E-9 | 0.000465 | 0 | 1.395 | ||
| 15 | 0 | 23 | 0 | 0.16030 | 3.59E-10 | 0.000182 | 0 | 1.427 |
| Optimization Results | |||
|---|---|---|---|
| Iterations | 15 | Function Calls | 24 |
| Jacobian Calls | 16 | Active Constraints | 0 |
| Objective Function | 0.1603035477 | Max Abs Gradient Element | 0.0001820805 |
| Lambda | 0 | Actual Over Pred Change | 1.4266532872 |
| Radius | 0.0010322573 | ||
| Fit Function | 0.1603 |
|---|---|
| Goodness of Fit Index (GFI) | 0.9530 |
| GFI Adjusted for Degrees of Freedom (AGFI) | 0.0120 |
| Root Mean Square Residual (RMR) | 2.0653 |
| Standardized Root Mean Square Residual (SRMR) | 0.0009 |
| Parsimonious GFI (Mulaik, 1989) | 0.0635 |
| Chi-Square | 3.0458 |
| Chi-Square DF | 1 |
| Pr > Chi-Square | 0.0809 |
| Independence Model Chi-Square | 534.27 |
| Independence Model Chi-Square DF | 15 |
| RMSEA Estimate | 0.3281 |
| RMSEA 90% Lower Confidence Limit | . |
| RMSEA 90% Upper Confidence Limit | 0.7777 |
| ECVI Estimate | 1.8270 |
| ECVI 90% Lower Confidence Limit | . |
| ECVI 90% Upper Confidence Limit | 3.3493 |
| Probability of Close Fit | 0.0882 |
| Bentler's Comparative Fit Index | 0.9961 |
| Normal Theory Reweighted LS Chi-Square | 2.8142 |
| Akaike's Information Criterion | 1.0458 |
| Bozdogan's (1987) CAIC | -0.9500 |
| Schwarz's Bayesian Criterion | 0.0500 |
| McDonald's (1989) Centrality | 0.9501 |
| Bentler & Bonett's (1980) Non-normed Index | 0.9409 |
| Bentler & Bonett's (1980) NFI | 0.9943 |
| James, Mulaik, & Brett (1982) Parsimonious NFI | 0.0663 |
| Z-Test of Wilson & Hilferty (1931) | 1.4250 |
| Bollen (1986) Normed Index Rho1 | 0.9145 |
| Bollen (1988) Non-normed Index Delta2 | 0.9962 |
| Hoelter's (1983) Critical N | 25 |
| Q | = | -0.2295 | * | P | + | 0.3100 | * | D | + | 93.6193 | * | Intercept | + | 1.0000 | E1 | |||||
| beta1 | gamma1 | alphal | ||||||||||||||||||
| P | = | 4.2140 | * | Q | + | -0.9305 | * | F | + | -1.5579 | * | Y | + | -218.9 | * | Intercept | + | 1.0000 | E2 | |
| _b | gamma2_b | gamma3_b | alpha2_b |
| Variances of Exogenous Variables | ||
|---|---|---|
| Variable | Parameter | Estimate |
| D | 10154 | |
| F | 9989 | |
| Y | 151.05263 | |
| Intercept | 1.05263 | |
| E1 | eps1 | 3.51274 |
| E2 | eps2 | 105.06746 |
| Covariances Among Exogenous Variables | |||
|---|---|---|---|
| Var1 | Var2 | Parameter | Estimate |
| D | F | 9994 | |
| D | Y | 1101 | |
| F | Y | 1046 | |
| D | Intercept | 102.66842 | |
| F | Intercept | 101.71053 | |
| Y | Intercept | 11.05263 | |
| E1 | E2 | eps3 | -18.87270 |
| Q | = | -0.2278 | * | P | + | 0.3016 | * | D | + | 0.9272 | * | Intercept | + | 0.0181 | E1 | |||||
| beta1 | gamma1 | alphal | ||||||||||||||||||
| P | = | 4.2467 | * | Q | + | -0.9048 | * | F | + | -0.1863 | * | Y | + | -2.1849 | * | Intercept | + | 0.0997 | E2 | |
| _b | gamma2_b | gamma3_b | alpha2_b |
| Squared Multiple Correlations | ||||
|---|---|---|---|---|
| Variable | Error Variance | Total Variance | R-Square | |
| 1 | Q | 3.51274 | 10730 | 0.9997 |
| 2 | P | 105.06746 | 10565 | 0.9901 |
You can obtain almost equivalent results by applying the SAS/ETS procedure SYSLIN to this problem.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.