| The CALIS Procedure |
| Output Data Sets |
OUTEST= SAS-data-set
The OUTEST= (or OUTVAR=) data set is of TYPE=EST and contains the final parameter estimates, the gradient, the Hessian, and boundary and linear constraints. For METHOD=ML, METHOD=GLS, and METHOD=WLS, the OUTEST= data set also contains the approximate standard errors, the information matrix (crossproduct Jacobian), and the approximate covariance matrix of the parameter estimates ((generalized) inverse of the information matrix). If there are linear or nonlinear equality or active inequality constraints at the solution, the OUTEST= data set also contains Lagrange multipliers, the projected Hessian matrix, and the Hessian matrix of the Lagrange function.
The OUTEST= data set can be used to save the results of an optimization by PROC CALIS for another analysis with either PROC CALIS or another SAS procedure. Saving results to an OUTEST= data set is advised for expensive applications that cannot be repeated without considerable effort.
The OUTEST= data set contains the BY variables, two character variables _TYPE_ and _NAME_,  numeric variables corresponding to the parameters used in the model, a numeric variable _RHS_ (right-hand side) that is used for the right-hand-side value
numeric variables corresponding to the parameters used in the model, a numeric variable _RHS_ (right-hand side) that is used for the right-hand-side value 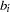 of a linear constraint or for the value
of a linear constraint or for the value 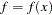 of the objective function at the final point
of the objective function at the final point 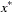 of the parameter space, and a numeric variable _ITER_ that is set to zero for initial values, set to the iteration number for the OUTITER output, and set to missing for the result output.
of the parameter space, and a numeric variable _ITER_ that is set to zero for initial values, set to the iteration number for the OUTITER output, and set to missing for the result output.
The _TYPE_ observations in Table 25.5 are available in the OUTEST= data set, depending on the request.
_TYPE_ |
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
ACTBC |
If there are active boundary constraints at the solution
|
||||||||||
COV |
contains the approximate covariance matrix of the parameter estimates; used in computing the approximate standard errors. |
||||||||||
COVRANK |
contains the rank of the covariance matrix of the parameter estimates. |
||||||||||
CRPJ_LF |
contains the Hessian matrix of the Lagrange function (based on CRPJAC). |
||||||||||
CRPJAC |
contains the approximate Hessian matrix used in the optimization process. This is the inverse of the information matrix. |
||||||||||
EQ |
If linear constraints are used, this observation contains the |
||||||||||
GE |
If linear constraints are used, this observation contains the |
||||||||||
GRAD |
contains the gradient of the estimates. |
||||||||||
GRAD_LF |
contains the gradient of the Lagrange function. The _RHS_ variable contains the value of the Lagrange function. |
||||||||||
HESSIAN |
contains the Hessian matrix. |
||||||||||
HESS_LF |
contains the Hessian matrix of the Lagrange function (based on HESSIAN). |
||||||||||
INFORMAT |
contains the information matrix of the parameter estimates (only for METHOD=ML, METHOD=GLS, or METHOD=WLS). |
||||||||||
INITIAL |
contains the starting values of the parameter estimates. |
||||||||||
JACNLC |
contains the Jacobian of the nonlinear constraints evaluated at the final estimates. |
||||||||||
JACOBIAN |
contains the Jacobian matrix (only if the OUTJAC option is used). |
||||||||||
LAGM BC |
contains Lagrange multipliers for masks and active boundary constraints.
|
||||||||||
LAGM LC |
contains Lagrange multipliers for linear equality and active inequality constraints in pairs of observations containing the constraint number and the value of the Lagrange multiplier.
|
||||||||||
LAGM NLC |
contains Lagrange multipliers for nonlinear equality and active inequality constraints in pairs of observations containing the constraint number and the value of the Lagrange multiplier.
|
||||||||||
LE |
If linear constraints are used, this observation contains the |
||||||||||
LOWERBD |
If boundary constraints are used, this observation contains the lower bounds. Those parameters not subjected to lower bounds contain missing values. The _RHS_ variable contains a missing value, and the _NAME_ variable is blank. |
||||||||||
NACTBC |
All parameter variables contain the number |
||||||||||
NACTLC |
All parameter variables contain the number |
||||||||||
NLC_EQ |
contains values and residuals of nonlinear constraints. The _NAME_ variable is described as follows.
|
||||||||||
NLDACTBC |
contains the number of active boundary constraints at the solution |
||||||||||
NLDACTLC |
contains the number of active linear constraints at the solution |
||||||||||
_NOBS_ |
contains the number of observations. |
||||||||||
PARMS |
contains the final parameter estimates. The _RHS_ variable contains the value of the objective function. |
||||||||||
PCRPJ_LF |
contains the projected Hessian matrix of the Lagrange function (based on CRPJAC). |
||||||||||
PHESS_LF |
contains the projected Hessian matrix of the Lagrange function (based on HESSIAN). |
||||||||||
PROJCRPJ |
contains the projected Hessian matrix (based on CRPJAC). |
||||||||||
PROJGRAD |
If linear constraints are used in the estimation, this observation contains the |
||||||||||
PROJHESS |
contains the projected Hessian matrix (based on HESSIAN). |
||||||||||
SIGSQ |
contains the scalar factor of the covariance matrix of the parameter estimates. |
||||||||||
STDERR |
contains approximate standard errors (only for METHOD=ML, METHOD=GLS, or METHOD=WLS). |
||||||||||
TERMINAT |
The _NAME_ variable contains the name of the termination criterion. |
||||||||||
UPPERBD |
If boundary constraints are used, this observation contains the upper bounds. Those parameters not subjected to upper bounds contain missing values. The _RHS_ variable contains a missing value, and the _NAME_ variable is blank. |
If the technique specified by the TECH= option cannot be performed (for example, no feasible initial values can be computed, or the function value or derivatives cannot be evaluated at the starting point), the OUTEST= data set might contain only some of the observations (usually only the PARMS and GRAD observations).
OUTRAM= SAS-data-set
The OUTRAM= data set is of TYPE=RAM and contains the model specification and the computed parameter estimates. This data set is intended to be reused as an INRAM= data set to specify good initial values in a subsequent analysis by PROC CALIS.
The OUTRAM= data set contains the following variables:
the BY variables, if any
the character variable _TYPE_, which takes the values MODEL, ESTIM, VARNAME, METHOD, and STAT
six additional variables whose meaning depends on the _TYPE_ of the observation
Each observation with _TYPE_=MODEL defines one matrix in the generalized COSAN model. The additional variables are as follows.
Variable |
Contents |
|---|---|
_NAME_ |
name of the matrix (character) |
_MATNR_ |
number for the term and matrix in the model (numeric) |
_ROW_ |
matrix row number (numeric) |
_COL_ |
matrix column number (numeric) |
_ESTIM_ |
first matrix type (numeric) |
_STDERR_ |
second matrix type (numeric) |
If the generalized COSAN model has only one matrix term, the _MATNR_ variable contains only the number of the matrix in the term. If there is more than one term, then it is the term number multiplied by 10,000 plus the matrix number (assuming that there are no more than 9,999 matrices specified in the COSAN model statement).
Each observation with _TYPE_=ESTIM defines one element of a matrix in the generalized COSAN model. The variables are used as follows.
Variable |
Contents |
|---|---|
_NAME_ |
name of the parameter (character) |
_MATNR_ |
term and matrix location of parameter (numeric) |
_ROW_ |
row location of parameter (numeric) |
_COL_ |
column location of parameter (numeric) |
_ESTIM_ |
parameter estimate or constant value (numeric) |
_STDERR_ |
standard error of estimate (numeric) |
For constants rather than estimates, the _STDERR_ variable is 0. The _STDERR_ variable is missing for ULS and DWLS estimates if NOSTDERR is specified or if the approximate standard errors are not computed.
Each observation with _TYPE_=VARNAME defines a column variable name of a matrix in the generalized COSAN model.
The observations with _TYPE_=METHOD and _TYPE_=STAT are not used to build the model. The _TYPE_=METHOD observation contains the name of the estimation method used to compute the parameter estimates in the _NAME_ variable. If METHOD=NONE is not specified, the _ESTIM_ variable of the _TYPE_=STAT observations contains the information summarized in Table 25.8 (described in the section Assessment of Fit).
_NAME_ |
_ESTIM_ |
|---|---|
N |
sample size |
NPARM |
number of parameters used in the model |
DF |
degrees of freedom |
N_ACT |
number of active boundary constraints |
for ML, GLS, and WLS estimation |
|
FIT |
fit function |
GFI |
goodness of fit index (GFI) |
AGFI |
adjusted GFI for degrees of freedom |
RMR |
root mean square residual |
SRMR |
standardized root mean square residual |
PGFI |
parsimonious GFI of Mulaik et al. (1989) |
CHISQUAR |
overall |
P_CHISQ |
probability |
CHISQNUL |
null (baseline) model |
RMSEAEST |
Steiger and Lind’s (1980) RMSEA index estimate |
RMSEALOB |
lower range of RMSEA confidence interval |
RMSEAUPB |
upper range of RMSEA confidence interval |
P_CLOSFT |
Browne and Cudeck’s (1993) probability of close fit |
ECVI_EST |
Browne and Cudeck’s (1993) ECV index estimate |
ECVI_LOB |
lower range of ECVI confidence interval |
ECVI_UPB |
upper range of ECVI confidence interval |
COMPFITI |
Bentler’s (1989) comparative fit index |
ADJCHISQ |
adjusted |
P_ACHISQ |
probability corresponding adjusted |
RLSCHISQ |
reweighted least squares |
AIC |
Akaike’s information criterion |
CAIC |
Bozdogan’s consistent information criterion |
SBC |
Schwarz’s Bayesian criterion |
CENTRALI |
McDonald’s centrality criterion |
PARSIMON |
Parsimonious index of James, Mulaik, and Brett |
ZTESTWH |
z test of Wilson and Hilferty |
BB_NONOR |
Bentler-Bonett (1980) nonnormed index |
BB_NORMD |
Bentler-Bonett (1980) normed index |
BOL_RHO1 |
Bollen’s (1986) normed index |
BOL_DEL2 |
Bollen’s (1989a) nonnormed index |
CNHOELT |
Hoelter’s critical N index |
You can edit the OUTRAM= data set to use its contents for initial estimates in a subsequent analysis by PROC CALIS, perhaps with a slightly changed model. But you should be especially careful for _TYPE_=MODEL when changing matrix types. The codes for the two matrix types are listed in Table 25.9.
Code |
First Matrix Type |
Description |
|---|---|---|
1: |
IDE |
identity matrix |
2: |
ZID |
zero matrix concatenated by an identity matrix |
3: |
DIA |
diagonal matrix |
4: |
ZDI |
zero matrix concatenated by a diagonal matrix |
5: |
LOW |
lower triangular matrix |
6: |
UPP |
upper triangular matrix |
7: |
temporarily not used |
|
8: |
SYM |
symmetric matrix |
9: |
GEN |
general-type matrix |
10: |
BET |
identity minus general-type matrix |
11: |
PER |
selection matrix |
12: |
first matrix ( |
|
13: |
second matrix ( |
|
14: |
third matrix ( |
|
Code |
Second Matrix Type |
Description |
0: |
noninverse model matrix |
|
1: |
INV |
inverse model matrix |
2: |
IMI |
"identity minus inverse" model matrix |
OUTSTAT= SAS-data-set
The OUTSTAT= data set is similar to the TYPE=COV, TYPE=UCOV, TYPE=CORR, or TYPE=UCORR data set produced by the CORR procedure. The OUTSTAT= data set contains the following variables:
the BY variables, if any
two character variables, _TYPE_ and _NAME_
the variables analyzed—that is, those in the VAR statement, or if there is no VAR statement, all numeric variables not listed in any other statement but used in the analysis. ( Caution:Using the LINEQS or RAM model statements selects variables automatically.)
The OUTSTAT= data set contains the following information (when available):
the mean and standard deviation
the skewness and kurtosis (if the DATA= data set is a raw data set and the KURTOSIS option is specified)
the number of observations
if the WEIGHT statement is used, sum of the weights
the correlation or covariance matrix to be analyzed
the predicted correlation or covariance matrix
the standardized or normalized residual correlation or covariance matrix
if the model contains latent variables, the predicted covariances between latent and manifest variables, and the latent variable (or factor) score regression coefficients (see the PLATCOV display option)
In addition, if the FACTOR model statement is used, the OUTSTAT= data set contains the following:
the unrotated factor loadings, the unique variances, and the matrix of factor correlations
the rotated factor loadings and the transformation matrix of the rotation
the matrix of standardized factor loadings
Each observation in the OUTSTAT= data set contains some type of statistic as indicated by the _TYPE_ variable. The values of the _TYPE_ variable are given in Table 25.10.
_TYPE_ |
Contents |
|---|---|
MEAN |
means |
STD |
standard deviations |
USTD |
uncorrected standard deviations |
SKEWNESS |
univariate skewness |
KURTOSIS |
univariate kurtosis |
N |
sample size |
SUMWGT |
sum of weights (if WEIGHT statement is used) |
COV |
covariances analyzed |
CORR |
correlations analyzed |
UCOV |
uncorrected covariances analyzed |
UCORR |
uncorrected correlations analyzed |
ULSPRED |
ULS predicted model values |
GLSPRED |
GLS predicted model values |
MAXPRED |
ML predicted model values |
WLSPRED |
WLS predicted model values |
DWLSPRED |
DWLS predicted model values |
ULSNRES |
ULS normalized residuals |
GLSNRES |
GLS normalized residuals |
MAXNRES |
ML normalized residuals |
WLSNRES |
WLS normalized residuals |
DWLSNRES |
DWLS normalized residuals |
ULSSRES |
ULS variance standardized residuals |
GLSSRES |
GLS variance standardized residuals |
MAXSRES |
ML variance standardized residuals |
WLSSRES |
WLS variance standardized residuals |
DWLSSRES |
DWLS variance standardized residuals |
ULSASRES |
ULS asymptotically standardized residuals |
GLSASRES |
GLS asymptotically standardized residuals |
MAXASRES |
ML asymptotically standardized residuals |
WLSASRES |
WLS asymptotically standardized residuals |
DWLSASRS |
DWLS asymptotically standardized residuals |
UNROTATE |
unrotated factor loadings |
FCORR |
matrix of factor correlations |
UNIQUE_V |
unique variances |
TRANSFOR |
transformation matrix of rotation |
LOADINGS |
rotated factor loadings |
STD_LOAD |
standardized factor loadings |
LSSCORE |
latent variable (or factor) score regression coefficients for ULS method |
SCORE |
latent variable (or factor) score regression coefficients other than ULS method |
The _NAME_ variable contains the name of the manifest variable corresponding to each row for the covariance, correlation, predicted, and residual matrices and contains the name of the latent variable in case of factor regression scores. For other observations, _NAME_ is blank.
The unique variances and rotated loadings can be used as starting values in more difficult and constrained analyses.
If the model contains latent variables, the OUTSTAT= data set also contains the latent variable score regression coefficients and the predicted covariances between latent and manifest variables. You can use the latent variable score regression coefficients with PROC SCORE to compute latent variable or factor scores. For details, see the section Latent Variable Scores.
If the analyzed matrix is a (corrected or uncorrected) covariance rather than a correlation matrix, the _TYPE_=STD or _TYPE_=USTD observation is not included in the OUTSTAT= data set. In this case, the standard deviations can be obtained from the diagonal elements of the covariance matrix. Dropping the _TYPE_=STD or _TYPE_=USTD observation prevents PROC SCORE from standardizing the observations before computing the factor scores.
OUTWGT= SAS-data-set
You can create an OUTWGT= data set that is of TYPE=WEIGHT and contains the weight matrix used in generalized, weighted, or diagonally weighted least squares estimation. The inverse of the weight matrix is used in the corresponding fit function. The OUTWGT= data set contains the weight matrix to which the WRIDGE= and the WPENALTY= options are applied. For unweighted least squares or maximum likelihood estimation, no OUTWGT= data set can be written. The last weight matrix used in maximum likelihood estimation is the predicted model matrix (observations with _TYPE_=MAXPRED) that is included in the OUTSTAT= data set.
For generalized and diagonally weighted least squares estimation, the weight matrices  of the OUTWGT= data set contain all elements
of the OUTWGT= data set contain all elements  , where the indices
, where the indices  and
and  correspond to all manifest variables used in the analysis. Let
correspond to all manifest variables used in the analysis. Let 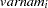 be the name of the
be the name of the  th variable in the analysis. In this case, the OUTWGT= data set contains
th variable in the analysis. In this case, the OUTWGT= data set contains  observations with variables as displayed in the following table.
observations with variables as displayed in the following table.
Variable |
Contents |
|---|---|
_TYPE_ |
WEIGHT (character) |
_NAME_ |
name of variable |
|
weight |
|
|
|
weight |
For weighted least squares estimation, the weight matrix  of the OUTWGT= data set contains only the nonredundant elements
of the OUTWGT= data set contains only the nonredundant elements  . In this case, the OUTWGT= data set contains
. In this case, the OUTWGT= data set contains 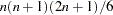 observations with variables as in the following table.
observations with variables as in the following table.
Variable |
Contents |
|---|---|
_TYPE_ |
WEIGHT (character) |
_NAME_ |
name of variable |
_NAM2_ |
name of variable |
_NAM3_ |
name of variable |
|
weight |
|
|
|
weight |
Symmetric redundant elements are set to missing values.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
 . The parameter variables contain the coefficients
. The parameter variables contain the coefficients  ,
, 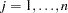 , the
, the  . The parameter variables contain the coefficients
. The parameter variables contain the coefficients 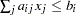 . The parameter variables contain the coefficients
. The parameter variables contain the coefficients 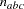 of active boundary constraints at the solution
of active boundary constraints at the solution 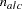 of active linear constraints at the solution
of active linear constraints at the solution 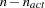 values of the projected gradient
values of the projected gradient 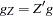 in the variables corresponding to the first
in the variables corresponding to the first 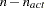 parameters. The
parameters. The 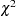
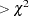
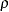
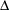

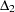
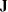 ) in LINEQS model statement
) in LINEQS model statement 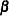 ) in LINEQS model statement
) in LINEQS model statement  ) in LINEQS model statement
) in LINEQS model statement 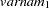
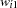 for variable
for variable 
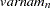
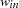 for variable
for variable 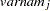 (character)
(character) 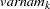 (character)
(character) 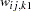 for variable
for variable 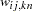 for variable
for variable