The HPLOGISTIC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Missing ValuesResponse DistributionsLog-Likelihood FunctionsExistence of Maximum Likelihood EstimatesUsing Validation and Test DataModel Fit and Assessment StatisticsThe Hosmer-Lemeshow Goodness-of-Fit TestComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names
Missing ValuesResponse DistributionsLog-Likelihood FunctionsExistence of Maximum Likelihood EstimatesUsing Validation and Test DataModel Fit and Assessment StatisticsThe Hosmer-Lemeshow Goodness-of-Fit TestComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names -
Examples

- References
MODEL Statement
-
MODEL response <(response-options)> = <effects> </ model-options>;
-
MODEL events / trials <(response-options)> = <effects> </ model-options>;
The MODEL statement defines the statistical model in terms of a response variable (the target) or an events/trials specification, model effects constructed from variables in the input data set, and options. An intercept is included in the model by default. You can remove the intercept with the NOINT option.
You can specify a single response variable that contains your binary, ordinal, or nominal response values. When you have binomial data, you can specify the events/trials form of the response, where one variable contains the number of positive responses (or events) and another variable contains the number of trials. Note that the values of both events and (trials – events) must be nonnegative and the value of trials must be positive.
For information about constructing the model effects, see the section Specification and Parameterization of Model Effects.
There are two sets of options in the MODEL statement. The response-options determine how the HPLOGISTIC procedure models probabilities for binary data. The model-options control other aspects of model formation and inference. Table 10.3 summarizes these options.
Table 10.3: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Response Variable Options |
|
|
Reverses the response categories |
|
|
Specifies the event category |
|
|
Specifies the sort order |
|
|
Specifies the reference category |
|
|
Model Options |
|
|
Specifies the confidence level for confidence limits |
|
|
Requests association statistics |
|
|
Requests confidence limits |
|
|
Requests classification statistics |
|
|
Specifies a cutpoint for binary classification |
|
|
Specifies the degrees-of-freedom method |
|
|
Includes effects in all models for model selection |
|
|
Requests the Hosmer and Lemeshow goodness-of-fit test |
|
|
Specifies the link function |
|
|
Suppresses checking for infinite parameters |
|
|
Suppresses the intercept |
|
|
Specifies the offset variable |
|
|
Specifies prior probabilities |
|
|
Requests a generalized coefficient of determination |
|
|
Includes effects in the initial model for model selection |
|
Response Variable Options
Response variable options determine how the HPLOGISTIC procedure models probabilities for binary and multinomial data.
You can specify the following response-options by enclosing them in parentheses after the response or trials variable.
Model Options

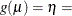
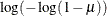
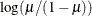
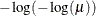
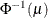
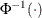
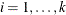
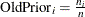
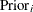
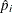
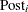
![\[ \mathrm{Post}_ i = \frac{\hat{p}_ i \frac{\mathrm{Prior}_ i}{\mathrm{OldPrior}_ i}}{\sum _{j=1}^ k\hat{p}_ j \frac{\mathrm{Prior}_ j}{\mathrm{OldPrior}_ j}} \]](images/stathpug_hplogistic0031.png)