The HPLOGISTIC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Missing ValuesResponse DistributionsLog-Likelihood FunctionsExistence of Maximum Likelihood EstimatesUsing Validation and Test DataModel Fit and Assessment StatisticsThe Hosmer-Lemeshow Goodness-of-Fit TestComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names
Missing ValuesResponse DistributionsLog-Likelihood FunctionsExistence of Maximum Likelihood EstimatesUsing Validation and Test DataModel Fit and Assessment StatisticsThe Hosmer-Lemeshow Goodness-of-Fit TestComputational Method: MultithreadingChoosing an Optimization AlgorithmDisplayed OutputODS Table Names -
Examples

- References
Using Validation and Test Data
When you have sufficient data, you can subdivide your data into three parts called the training, validation, and test data. During the selection process, models are fit on the training data, and the prediction errors for the models so obtained are found by using the validation data. This prediction error on the validation data can be used to decide when to terminate the selection process and to decide which model. Finally, after a selected model has been obtained, the test set can be used to assess how the selected model generalizes on data that played no role in selecting the model.
In some cases you might want to use only training and test data. For example, you might decide to use an information criterion to decide which effects to include and when to terminate the selection process. In this case no validation data are required, but test data can still be useful in assessing the predictive performance of the selected model. In other cases you might decide to use validation data during the selection process but forgo assessing the selected model on test data. Hastie, Tibshirani, and Friedman (2001) note that it is difficult to provide a general rule for how many observations you should assign to each role. They note that a typical split might be 50% for training and 25% each for validation and testing.
You use a PARTITION
statement to logically subdivide the DATA=
data set into separate roles. You can specify the fractions of the data that you want to reserve as test data and validation
data. For example, the following statements randomly subdivide the inData data set, reserving 50% for training and 25% each for validation and testing:
proc hplogistic data=inData; partition fraction(test=0.25 validate=0.25); ... run;
You can specify the SEED= option in the PARTITION statement to create the same partition data sets for a given number of compute nodes. However, changing the number of compute nodes changes the initial distribution of data, resulting in different partition data sets.
In some cases you might need to exercise more control over the partitioning of the input data set. You can do this by naming
both a variable in the input data set and a formatted value of that variable for each role. For example, the following statements
assign roles to the observations in the inData data set that are based on the value of the variable Group in that data set. Observations whose value of Group is Group 1 are assigned for testing, and those whose value is Group 2 are assigned to training. All other observations are ignored.
proc hplogistic data=inData; partition roleVar=Group(test='Group 1' train='Group 2') ... run;
When you have reserved observations for training, validation, and testing, a model that is fit on the training data is scored on the validation and test data, and statistics are computed separately for each of these subsets. For more information, see the section Partition Fit Statistics. For an illustration, see Example 10.4.
Using the Validation Statistic as the CHOOSE= Criterion
When you specify the CHOOSE= VALIDATE suboption of the METHOD= option in the SELECTION statement, the ASE is computed on the validation data for the models at each step of the selection process. The smallest model at any step that yields the smallest validation ASE is selected.
Using the Validation Statistic as the STOP= Criterion
When you specify the STOP= VALIDATE suboption of the METHOD= option in the SELECTION statement, the ASE is computed on the validation data for the models at each step of the selection process. At step k of the selection process, the best candidate effect to enter or leave the current model is determined and the validation ASE for this new model is computed. If this validation ASE is greater than the validation ASE for the model at step k, then the selection process terminates at step k.
Partition Fit Statistics
Specifying a PARTITION
statement modifies the display of many tables by adding separate rows or columns for the training, validation, and test data
sets. A "Partition Fit Statistics" table is also produced, and it displays the following statistics, which are useful for
assessing the model and which should be very similar for the different roles when the training data are representative of
the other data sets: average square error, misclassification rate, 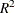 , max-rescaled
, max-rescaled 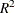 , and McFadden’s
, and McFadden’s 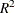 . Binary and binomial response models also display the following statistics: area under the ROC curve, the Hosmer-Lemeshow
test p-value, difference of means, Somers’ D statistic, and the true positive and negative fractions. Polytomous response models also display the true fraction for each
response level. For more information, see the sections Model Fit and Assessment Statistics and The Hosmer-Lemeshow Goodness-of-Fit Test.
. Binary and binomial response models also display the following statistics: area under the ROC curve, the Hosmer-Lemeshow
test p-value, difference of means, Somers’ D statistic, and the true positive and negative fractions. Polytomous response models also display the true fraction for each
response level. For more information, see the sections Model Fit and Assessment Statistics and The Hosmer-Lemeshow Goodness-of-Fit Test.