The HPFMM Procedure

Notation for the Finite Mixture Model

Subsections:

The general expression for the finite mixture model fitted with the HPFMM procedure is as follows:

$f(y) = \sum _{j=1}^{k} \pi _ j(\mb{z},\balpha _ j) p_ j(y;\mb{x}_ j’\bbeta _ j,\phi _ j)$

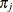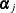The number of components in the mixture is denoted as k. The mixture probabilities $\pi _ j$ can depend on regressor variables $\mb{z}$ and parameters $\balpha _ j$ . By default, the HPFMM procedure models these probabilities using a logit transform if k = 2 and as a generalized logit model if k > 2. The component distributions 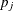$p_ j$ can also depend on regressor variables in 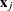$\mb{x}_ j$ , regression parameters 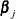$\bbeta _ j$ , and possibly scale parameters 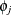$\phi _ j$ . Notice that the component distributions 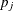$p_ j$ are indexed by j since the distributions might belong to different families. For example, in a two-component model, you might model one component as a normal (Gaussian) variable and the second component as a variable with a t distribution with low degrees of freedom to manage overdispersion.

The mixture probabilities 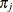$\pi _ j$ satisfy 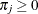$\pi _ j \ge 0$ , for all j, and

$\sum _{j=1}^{k} \pi _ j(\mb{z},\balpha _ j) = 1$