The HPFMM Procedure
Homogeneous Mixtures
If the component distributions are of the same distributional form, the mixture is called homogeneous. In most applications of homogeneous mixtures, the mixing probabilities do not depend on regression parameters. The general model then simplifies to
![\[ f(y) = \sum _{j=1}^{k} \pi _ j p(y;\mb{x}’\bbeta _ j,\phi _ j) \]](images/stathpug_hpfmm0011.png)
Since the component distributions depend on regression parameters 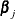 , this model is known as a homogeneous regression mixture. A homogeneous regression mixture assumes that the regression effects
are the same across the components, although the HPFMM procedure does not impose such a restriction. If the component distributions
do not contain regression effects, the model
, this model is known as a homogeneous regression mixture. A homogeneous regression mixture assumes that the regression effects
are the same across the components, although the HPFMM procedure does not impose such a restriction. If the component distributions
do not contain regression effects, the model
![\[ f(y) = \sum _{j=1}^{k} \pi _ j p(y;\mu _ j,\phi _ j) \]](images/stathpug_hpfmm0012.png)
is the homogeneous mixture model. A classical case is the estimation of a continuous density as a k-component mixture of normal distributions.
