-
ABSCONV=r
-
specifies an absolute function convergence criterion. For minimization, termination requires 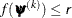 , where
, where 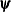 is the vector of parameters in the optimization and
is the vector of parameters in the optimization and 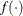 is the objective function. The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.
is the objective function. The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.
-
ABSFCONV=r
-
specifies an absolute function difference convergence criterion. For all techniques except Nelder–Mead simplex (NMSIMP), termination
requires a small change of the function value in successive iterations:
Here, 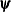 denotes the vector of parameters that participate in the optimization and
denotes the vector of parameters that participate in the optimization and 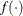 is the objective function. The same formula is used for the NMSIMP technique, but
is the objective function. The same formula is used for the NMSIMP technique, but 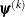 is defined as the vertex with the lowest function value and
is defined as the vertex with the lowest function value and 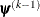 is defined as the vertex with the highest function value in the simplex. The default value is
is defined as the vertex with the highest function value in the simplex. The default value is 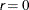 .
.
-
ABSGCONV=r
-
specifies an absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small:
Here, 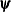 denotes the vector of parameters that participate in the optimization and
denotes the vector of parameters that participate in the optimization and 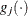 is the gradient of the objective function with respect to the
is the gradient of the objective function with respect to the 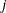 parameter. This criterion is not used by the NMSIMP technique. The default value is r=1E–5.
parameter. This criterion is not used by the NMSIMP technique. The default value is r=1E–5.
-
BLUP<(suboptions)>
-
requests that best linear unbiased predictions (BLUPs) for the random effects be displayed. To use this option, you must also
use the PARMS statement to specify fixed values for the covariance parameters, which means that the NOITER option in the PARMS
statement will be implied by the BLUP option. Also, the iterations in the ODS Table IterHistory will refer to iterations used
to compute the BLUP rather than optimization iterations.
The BLUP solution might be sensitive to the order of observations, and hence to how the data are distributed on the grid.
If there are multiple measures of a repeated effect, then the BLUP solution is not unique. If the order of these multiple
measures on the grid differs for different runs, then different BLUP solutions will result.
You can specify the following suboptions:
- ITPRINT=number
-
specifies that the iteration history be displayed after every number of iterations. The default value is 10, which means the procedure displays the iteration history for every 10 iterations.
- MAXITER=number
-
specifies the maximum number of iterations allowed. The default value is the number of parameters in the BLUP option plus
2.
- TOL=number
-
specifies the tolerance value. The default value is the square root of machine precision.
-
DATA=SAS-data-set
-
names the SAS data set to be used as the input data set. The default is the most recently created data set.
-
FCONV=r
-
specifies a relative function convergence criterion. For all techniques except NMSIMP, termination requires a small relative
change of the function value in successive iterations,
Here, 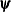 denotes the vector of parameters that participate in the optimization and
denotes the vector of parameters that participate in the optimization and 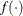 is the objective function. The same formula is used for the NMSIMP technique, but
is the objective function. The same formula is used for the NMSIMP technique, but 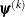 is defined as the vertex with the lowest function value and
is defined as the vertex with the lowest function value and 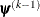 is defined as the vertex with the highest function value in the simplex.
is defined as the vertex with the highest function value in the simplex.
The default is 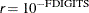 , where FDIGITS is
, where FDIGITS is 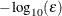 and
and  is the machine precision.
is the machine precision.
-
GCONV=r
-
specifies a relative gradient convergence criterion. For all techniques except CONGRA and NMSIMP, termination requires that
the normalized predicted function reduction be small,
Here, 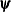 denotes the vector of parameters that participate in the optimization,
denotes the vector of parameters that participate in the optimization, 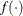 is the objective function, and
is the objective function, and 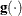 is the gradient. For the CONGRA technique (where a reliable Hessian estimate
is the gradient. For the CONGRA technique (where a reliable Hessian estimate 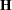 is not available), the following criterion is used:
is not available), the following criterion is used:
This criterion is not used by the NMSIMP technique. The default value is r=1E–8.
-
MAXCLPRINT=number
-
specifies the maximum levels of CLASS variables to print in the ODS table “ClassLevels.” The default value is 20. MAXCLPRINT=0 enables you to print all levels of each CLASS variable. However, the option NOCLPRINT takes precedence over MAXCLPRINT.
-
MAXFUNC=n
-
specifies the maximum number  of function calls in the optimization process. The default values are as follows, depending on the optimization technique:
of function calls in the optimization process. The default values are as follows, depending on the optimization technique:
The optimization can terminate only after completing a full iteration. Therefore, the number of function calls that are actually
performed can exceed n. You can choose the optimization technique with the TECHNIQUE= option.
-
MAXITER=n
-
specifies the maximum number  of iterations in the optimization process. The default values are as follows, depending on the optimization technique:
of iterations in the optimization process. The default values are as follows, depending on the optimization technique:
These default values also apply when  is specified as a missing value. You can choose the optimization technique with the TECHNIQUE= option.
is specified as a missing value. You can choose the optimization technique with the TECHNIQUE= option.
-
MAXTIME=r
-
specifies an upper limit of  seconds of CPU time for the optimization process. The default value is the largest floating-point double representation of
your computer. The time specified by the MAXTIME= option is checked only once at the end of each iteration. Therefore, the
actual running time can be longer than r.
seconds of CPU time for the optimization process. The default value is the largest floating-point double representation of
your computer. The time specified by the MAXTIME= option is checked only once at the end of each iteration. Therefore, the
actual running time can be longer than r.
-
METHOD=REML
METHOD=ML
-
specifies the estimation method for the covariance parameters. METHOD=REML performs residual (restricted) maximum likelihood;
it is the default method. METHOD=ML performs maximum likelihood.
-
MINITER=n
-
specifies the minimum number of iterations. The default value is 0. If you request more iterations than are actually needed
for convergence to a stationary point, the optimization algorithms can behave strangely. For example, the effect of rounding
errors can prevent the algorithm from continuing for the required number of iterations.
-
NAMELEN=number
-
specifies the length to which long effect names are shortened. The minimum value is 20, which is also the default.
-
NOCLPRINT<=number>
-
suppresses the display of the “Class Level Information” table if you do not specify number. If you specify number, the values of the classification variables are displayed for only those variables whose number of levels is less than number. Specifying a number helps to reduce the size of the “Class Level Information” table if some classification variables have a large number of levels.
-
NOPRINT
-
suppresses the generation of ODS output.
-
RANKS
-
displays the rank of design matrix
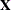 .
.
-
SINGCHOL=number
-
tunes the singularity criterion in Cholesky decompositions. The default is 1E4 times the machine epsilon; this product is
approximately 1E–12 on most computers.
-
SINGSWEEP=number
-
tunes the singularity criterion for sweep operations. The default is 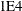 times the machine epsilon; this product is approximately 1E–12 on most computers.
times the machine epsilon; this product is approximately 1E–12 on most computers.
-
SINGULAR=number
-
tunes the general singularity criterion applied by the HPLMIXED procedure in sweeps and inversions. The default is 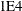 times the machine epsilon; this product is approximately 1E–12 on most computers.
times the machine epsilon; this product is approximately 1E–12 on most computers.
-
SPARSE
-
specifies the sparse technique is used together with BLUP option. In general, this option makes PROC HPLMIXED to be more efficient in terms of timing and memory. It supports the following
covariance types in RANDOM statement: VC, AR, CS, UC, UCH, CSH, UN CHOL and TOEP(1).
-
TECHNIQUE=keyword
-
specifies the optimization technique for obtaining maximum likelihood estimates. You can specify any of the following keywords:
- CONGRA
-
performs a conjugate-gradient optimization.
- DBLDOG
-
performs a version of double-dogleg optimization.
- NEWRAP
-
performs a Newton-Raphson optimization combining a line-search algorithm with ridging.
- NMSIMP
-
performs a Nelder-Mead simplex optimization.
- NONE
-
performs no optimization.
- NRRIDG
-
performs a Newton-Raphson optimization with ridging.
- QUANEW
-
performs a dual quasi-Newton optimization.
- TRUREG
-
performs a trust-region optimization.
The default value is TECHNIQUE=NRRIDG.
-
XCONV=r
-
specifies the relative parameter convergence criterion:
-
For all techniques except NMSIMP, termination requires a small relative parameter change in subsequent iterations:
-
For the NMSIMP technique, the same formula is used, but 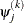 is defined as the vertex with the lowest function value and
is defined as the vertex with the lowest function value and 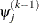 is defined as the vertex with the highest function value in the simplex.
is defined as the vertex with the highest function value in the simplex.
The default value is r = 1E–8 for the NMSIMP technique and r = 0 otherwise.

![\[ \frac{\max _ j |\psi _ j^{(k)} - \psi _ j^{(k-1)}| }{\max (|\psi _ j^{(k)}|,|\psi _ j^{(k-1)}|)} \leq \Argument{r} \]](images/stathpug_hplmixed0043.png)