Multivariate Analyses

Method

Observations with missing values for any of the Partial variables are not used. Observations with Weight or Freq values that are missing or that are less than or equal to 0 are not used. Only the integer part of Freq values is used.

Observations with missing values for Y or X variables are not used in the analysis except for the computation of pairwise correlations. Pairwise correlations are computed from all observations that have nonmissing values for any pair of variables.

The following notation is used in this chapter:

n is the number of nonmissing observations.
n_p, n_y, and n_x are the numbers of Partial, Y, and X variables.
d is the variance divisor.
w_i is the ith observation weight (values of the Weight variable).
y_i and x_i are the ith observed nonmissing Y and X vectors.
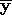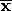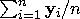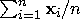${{\overline y}}$ and ${{\overline x}}$ are the sample mean vectors, ${\sum_{i=1}^n{y_{i} / n}}$ , ${\sum_{i=1}^n{x_{i} / n}}$ .

The sums of squares and crossproducts of the variables are

${ U_{yy} = \sum_{i=1}^n{ y_{i} { y_{i}'}} }$
${ U_{yx} = \sum_{i=1}^n{ y_{i} { x_{i}'}} }$
${ U_{xx} = \sum_{i=1}^n{ x_{i} { x_{i}'}} }$

The corrected sums of squares and crossproducts of the variables are

${ C_{yy} = \sum_{i=1}^n{( y_{i} - {\overline y}) {( y_{i}-{\overline y})'}} }$
${ C_{yx} = \sum_{i=1}^n{( y_{i} - {\overline y}) {( x_{i}-{\overline x})'}} }$
${ C_{xx} = \sum_{i=1}^n{( x_{i} - {\overline x}) {( x_{i}-{\overline x})'}} }$

If you select a Weight variable, the sample mean vectors are

${{\overline y} = \sum_{i=1}^n{w_{i} y_{i}} / \sum_{i=1}^n{w_{i}} }$ ${{\overline x} = \sum_{i=1}^n{w_{i} x_{i}} / \sum_{i=1}^n{w_{i}} }$

The sums of squares and crossproducts with a Weight variable are

${ U_{yy} = \sum_{i=1}^n{ w_{i} y_{i} { y_{i}'}} }$
${ U_{yx} = \sum_{i=1}^n{ w_{i} y_{i} { x_{i}'}} }$
${ U_{xx} = \sum_{i=1}^n{ w_{i} x_{i} { x_{i}'}} }$

The corrected sums of squares and crossproducts with a Weight variable are

${ C_{yy} = \sum_{i=1}^n{ w_{i} ( y_{i} - {\overline y}) {( y_{i}-{\overline y})'}} }$
${ C_{yx} = \sum_{i=1}^n{ w_{i} ( y_{i} - {\overline y}) {( x_{i}-{\overline x})'}} }$
${ C_{xx} = \sum_{i=1}^n{ w_{i} ( x_{i} - {\overline x}) {( x_{i}-{\overline x})'}} }$

The covariance matrices are computed as

S_yy = C_yy / d S_yx = C_yx / d S_xx = C_xx / d

To view or change the variance divisor d used in the calculation of variances and covariances, or to view or change other method options in the multivariate analysis, click on the Method button from the variables dialog to display the method options dialog.

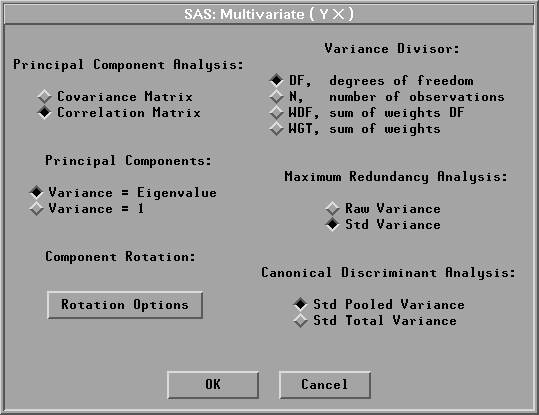
Figure 40.3: Multivariate Method Options Dialog

The variance divisor d is defined as

$\bullet {d = n-n_{p}-1}$		for vardef=DF, degrees of freedom
$\bullet {d = n}$		for vardef=N, number of observations
$\bullet {d = \sum_{i}^{}{w_{i}}-n_{p}-1}$		for vardef=WDF, sum of weights minus number of partial variables minus 1
$\bullet {d = \sum_{i}^{}{w_{i}}}$		for vardef=WGT, sum of weights

By default, SAS/INSIGHT software uses DF, degrees of freedom.

The correlation matrices R_yy, R_yx, and R_xx, containing the Pearson product-moment correlations of the variables, are derived by scaling their corresponding covariance matrices:

R_yy = D_yy^-1 S_yy D_yy^-1
R_yx = D_yy^-1 S_yx D_xx^-1
R_xx = D_xx^-1 S_xx D_xx^-1

where D_yy and D_xx are diagonal matrices whose diagonal elements are the square roots of the diagonal elements of S_yy and S_xx:

D_yy = (diag( S_yy))^1/2
D_xx = (diag( S_xx))^1/2

Method

Principal Component Analysis

Principal Component Rotation

Canonical Correlation Analysis

Maximum Redundancy Analysis

Canonical Discriminant Analysis