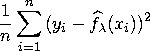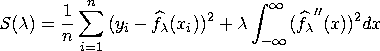Nonparametric Smoothing Spline

Fit Analyses

Nonparametric Smoothing Spline

Two criteria can be used to select an estimator ${\hat{f_\lambda}}$ for the function f:

goodness of fit to the data
smoothness of the fit

A standard measure of goodness of fit is the mean residual sum of squares

$\frac{1}n\sum_{i=1}^n{( y_{i}- \hat{f_\lambda}( x_{i}))^2}$

A measure of the smoothness of a fit is the integrated squared second derivative

$\int_{-{\infty}}^{{\infty}}{( {\hat{f_\lambda}"}(x))^2 dx}$

A single criterion that combines the two criteria is then given by

$S(\lambda) = \frac{1}n \sum_{i=1}^n{( y_{i}- \hat{f_\lambda}( x_{i}))^2} + \lambda\int_{-{\infty}}^{{\infty}}{( {\hat{f_\lambda}"}(x) )^2 dx}$

where ${\hat{f_\lambda}}$ belongs to the set of all continuously differentiable functions with square integrable second derivatives, and $\lambda$ is a positive constant.

The estimator that results from minimizing S( $\lambda$ )is called the smoothing spline estimator. This estimator fits a cubic polynomial in each interval between points. At each point x_i, the curve and its first two derivatives are continuous (Reinsch 1967).

The smoothing parameter $\lambda$ controls the amount of smoothing; that is, it controls the trade-off between the goodness of fit to the data and the smoothness of the fit. You select a smoothing parameter $\lambda$ by specifying a constant c in the formula

$\lambda = (Q / 10)^3 c$

where Q is the interquartile range of the explanatory variable. This formulation makes c independent of the units of X.

After choosing Curves:Spline, you specify a smoothing parameter selection method in the Spline Fit dialog.

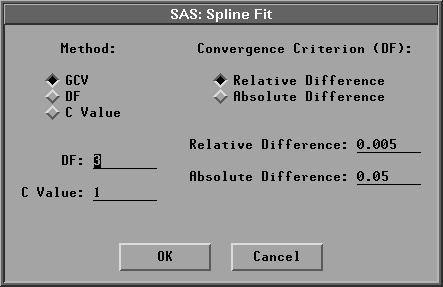
Figure 39.40: Spline Fit Dialog

The default Method:GCV uses a c value that minimizes the generalized cross validation mean squared error ${ \rm{MSE}_{GCV}(\lambda)}$ .Figure 39.41 displays smoothing spline estimates with c values of 0.0017 (the GCV value) and 15.2219 (DF=3). Use the slider in the table to change the c value of the spline fit.

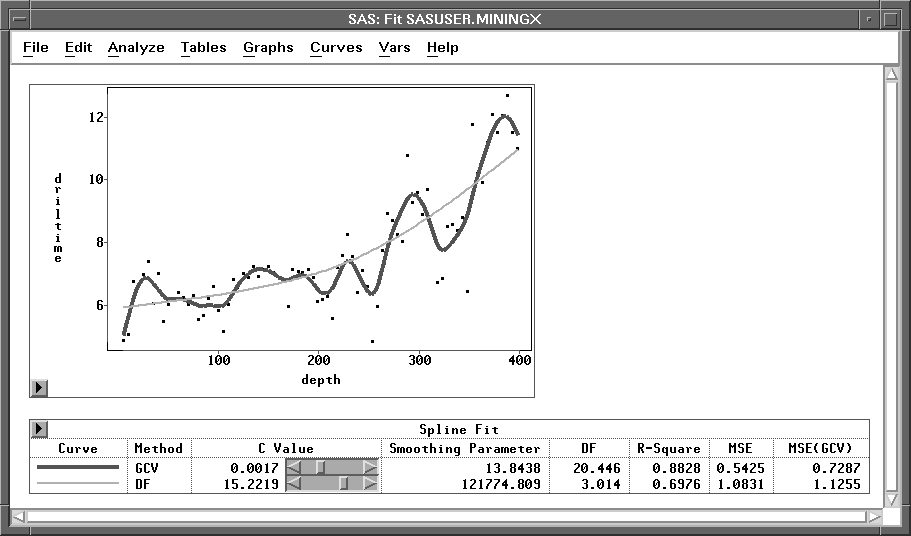
Figure 39.41: Smoothing Spline Estimates

Top of Page