Parametric Curves: Confidence Curves

Fit Analyses

Parametric Curves: Confidence Curves

You can add two types of confidence curves for the predicted values. One curve is for the mean value of the response, and the other is for the prediction of a new observation.

For the ith observation, a confidence interval that covers the expected value of the response with probability $1-\alpha$ has upper and lower limits

$x_{i} b \, {+-} \, t_{(1-\alpha/2)} \sqrt{ h_{i}} s$

where $t_{(1-\alpha/2)}$ is the $(1-\alpha/2)$ critical value of the Student's t statistic with degrees of freedom equal to the degrees of freedom for the mean squared error and h_i is the ith diagonal element of the hat matrix H. The hat matrix H is described in the section "Output Variables" later in this chapter.

The $100(1-\alpha)\%$ upper and lower limits for prediction are

$x_{i} b \, {+-} \, t_{(1-\alpha/2)} \sqrt{1+ h_{i}} s$

You can generate confidence curves for a parametric regression fit by choosing the confidence coefficient from the Curves:Confidence Curves menu.

[menu]
Figure 39.38: Confidence Curves Menu

Figure 39.39 displays a quadratic polynomial fit with 95% mean confidence curves for the response. Use the Coefficient slider to change the confidence coefficient.

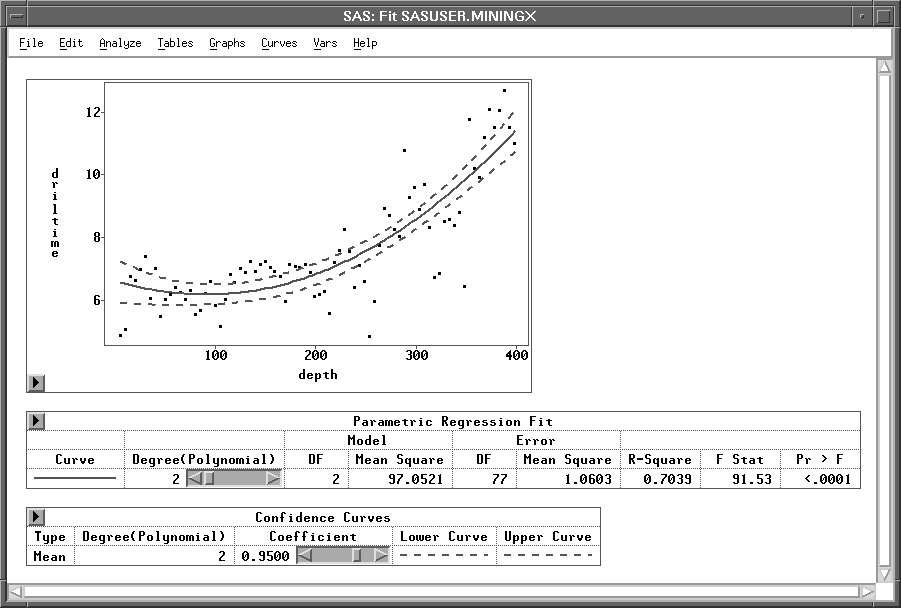
Figure 39.39: A Quadratic Polynomial Fit with 99% Mean Confidence Curves

Top of Page