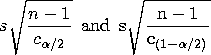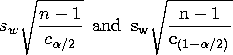Basic Confidence Intervals

Distribution Analyses

Basic Confidence Intervals

Assuming that the population is normally distributed, the Confidence Intervals table gives confidence intervals for the mean, standard deviation, and variance at the confidence coefficient specified. You specify the confidence intervals either in the distribution output options dialog or from the Tables menu.

[menu]

Figure 38.10: Basic Confidence Intervals Menu

The $100(1-\alpha)\%$ confidence interval for the mean has upper and lower limits

${\overline y} {+-} t_{(1 - \alpha/2)} \frac{s}{\sqrt{n}}$

where $t_{(1 - \alpha/2)}$ is the $(1-\alpha/2)$ critical value of the Student's t statistic with n-1 degrees of freedom.

For weighted analyses, the limits are

${\overline y_{w}} {+-} t_{(1 - \alpha/2)} \frac{s_{w}} {\sqrt{\sum_{i}^{}{w_{i}}} }$

For large values of n, $t_{(1 - \alpha/2)}$ acts as $z_{(1 - \alpha/2)}$ ,the $(1-\alpha/2)$ critical value of the standard normal distribution.

The $100(1-\alpha)\%$ confidence interval for the standard deviation has upper and lower limits

$s \sqrt{\frac{n-1}{c_{\alpha/2}}} \,\,\, \rm{and}\,\,\, s \sqrt{\frac{n-1}{c_{(1-\alpha/2)}}}$

where $c_{\alpha/2}$ and $c_{(1-\alpha/2)}$ are the $\alpha/2$ and $(1-\alpha/2)$ critical values of the chi-square distribution with n-1 degrees of freedom.

For weighted analyses, the limits are

$s_{w}\sqrt{\frac{n-1}{c_{\alpha/2}}} \,\,\,\rm{and}\,\,\, s_{w}\sqrt{\frac{n-1}{c_{(1-\alpha/2)}}}$

The $100(1-\alpha)\%$ confidence interval for the variance has upper and lower limits equal to the squares of the corresponding upper and lower limits for the standard deviation.

Figure 38.11 shows a table of the 95% confidence intervals for the mean, standard deviation, and variance.

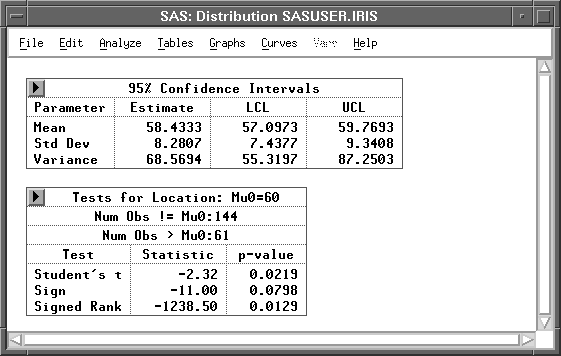
Figure 38.11: Basic Confidence Intervals and Tests for Location Tables

Note	The confidence intervals are set to missing if vardef ${\ne}$ DF.

Top of Page