PCHART Statement: SHEWHART Procedure
Example 18.26 OC Curve for Chart
Note: See OC Curve for a p Chart in the SAS/QC Sample Library.
This example uses the GPLOT procedure and the OUTLIMITS= data set Faillim2 from the previous example to plot an OC curve for the p chart shown in Output 18.25.3.
The OC curve displays 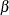 (the probability that
(the probability that 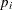 lies within the control limits) as a function of p (the true proportion nonconforming). The computations are exact, assuming that the process is in control and that the number
of nonconforming items (
lies within the control limits) as a function of p (the true proportion nonconforming). The computations are exact, assuming that the process is in control and that the number
of nonconforming items (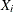 ) has a binomial distribution.
) has a binomial distribution.
The value of 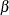 is computed as follows:
is computed as follows:
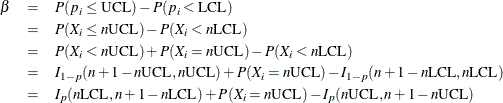
Here, 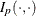 denotes the incomplete beta function. The following DATA step computes
denotes the incomplete beta function. The following DATA step computes 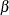 (the variable BETA) as a function of p (the variable
(the variable BETA) as a function of p (the variable p):
data ocpchart;
set Faillim2;
keep beta fraction _lclp_ _p_ _uclp_;
nucl=_limitn_*_uclp_;
nlcl=_limitn_*_lclp_;
do p=0 to 500;
fraction=p/1000;
if nucl=floor(nucl) then
adjust=probbnml(fraction,_limitn_,nucl) -
probbnml(fraction,_limitn_,nucl-1);
else adjust=0;
if nlcl=0 then
beta=1 - probbeta(fraction,nucl,_limitn_-nucl+1) + adjust;
else beta=probbeta(fraction,nlcl,_limitn_-nlcl+1) -
probbeta(fraction,nucl,_limitn_-nucl+1) +
adjust;
if beta >= 0.001 then output;
end;
call symput('lcl', put(_lclp_,5.3));
call symput('mean',put(_p_, 5.3));
call symput('ucl', put(_uclp_,5.3));
run;
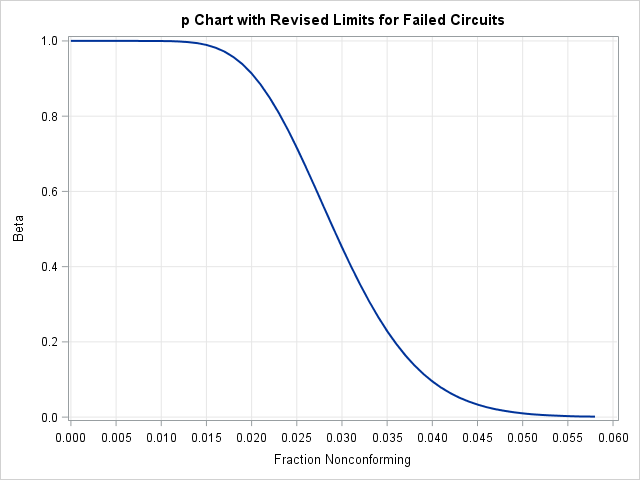
The following statements display the OC curve shown in Output 18.26.1:
proc sgplot data=ocpchart;
series x=fraction y=beta / lineattrs=(thickness=2);
xaxis values=(0 to 0.06 by 0.005) grid;
yaxis grid;
label fraction = 'Fraction Nonconforming'
beta = 'Beta';
run;
Output 18.26.1: OC Curve for p Chart