CDFPLOT Statement: CAPABILITY Procedure
The following entries provide detailed descriptions of the options specific to the CDFPLOT statement. The notes Traditional Graphics and Line Printer identify options that can be used only with traditional graphics and line printer plots, respectively. See Dictionary of Common Options: CAPABILITY Procedure for detailed descriptions of options common to all the plot statements.
- ALPHA=value
-
specifies the shape parameter
 for distribution functions requested with the BETA, GAMMA, PARETO, and POWER options. Enclose the ALPHA= option in parentheses after the distribution keyword. If you do not specify a value for
for distribution functions requested with the BETA, GAMMA, PARETO, and POWER options. Enclose the ALPHA= option in parentheses after the distribution keyword. If you do not specify a value for  , the procedure calculates a maximum likelihood estimate. For examples, see the entries for the distribution options.
, the procedure calculates a maximum likelihood estimate. For examples, see the entries for the distribution options.
- BETA<(beta-options)>
-
displays a fitted beta distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for $x \leq \theta $} \\ I_{\frac{x - \theta }{\sigma }} (\alpha , \beta ) & \mbox{for $\theta < x < \theta + \sigma $} \\ 1 & \mbox{for $x \geq \sigma + \theta $} \end{array} \right. \]](images/qcug_capability0329.png)
where
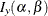 is the incomplete beta function, and
is the incomplete beta function, and
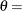 lower threshold parameter (lower endpoint)
lower threshold parameter (lower endpoint) 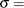 scale parameter
scale parameter 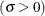
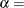 shape parameter
shape parameter 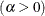
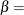 shape parameter
shape parameter 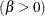
The beta distribution is bounded below by the parameter
 and above by the value
and above by the value 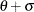 . You can specify
. You can specify  and
and  by using the THETA= and SIGMA= beta-options, as illustrated in the following statements, which fit a beta distribution bounded between 50 and 75. The default values for
by using the THETA= and SIGMA= beta-options, as illustrated in the following statements, which fit a beta distribution bounded between 50 and 75. The default values for  and
and  are 0 and 1, respectively.
are 0 and 1, respectively.
proc capability; cdfplot / beta(theta=50 sigma=25); run;
The beta distribution has two shape parameters,
 and
and 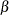 . If these parameters are known, you can specify their values with the ALPHA= and BETA= beta-options. If you do not specify values for
. If these parameters are known, you can specify their values with the ALPHA= and BETA= beta-options. If you do not specify values for  and
and 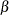 , the procedure calculates maximum likelihood estimates.
, the procedure calculates maximum likelihood estimates.
The BETA option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the BETA distribution option.
-
BETA=value
B=value -
specifies the second shape parameter
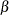 for beta distribution functions requested by the BETA option. Enclose the BETA= option in parentheses after the BETA keyword.
If you do not specify a value for
for beta distribution functions requested by the BETA option. Enclose the BETA= option in parentheses after the BETA keyword.
If you do not specify a value for 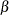 , the procedure calculates a maximum likelihood estimate. For examples, see the preceding entry for the BETA option.
, the procedure calculates a maximum likelihood estimate. For examples, see the preceding entry for the BETA option.
- C=value
-
specifies the shape parameter c for Weibull distribution functions requested with the WEIBULL option. Enclose the C= option in parentheses after the WEIBULL keyword. If you do not specify a value for c, the procedure calculates a maximum likelihood estimate. You can specify the SHAPE= option as an alias for the C= option.
- CDFSYMBOL='character'
-
Line Printerspecifies the character used to plot the points on cdf line printer plots. The default is the plus sign (+). Use the SYMBOL statement to control the plotting symbol in graphical output.
-
EXPONENTIAL<(exponential-options)>
EXP<(exponential-options )> -
displays a fitted exponential distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for $x \leq \theta $} \\ 1 - \exp \left(-\frac{x - \theta }{\sigma } \right) & \mbox{for $x > \theta $ } \end{array} \right. \]](images/qcug_capability0339.png)
where
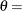 threshold parameter
threshold parameter 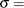 scale parameter
scale parameter 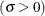
The parameter
 must be less than or equal to the minimum data value. You can specify
must be less than or equal to the minimum data value. You can specify  with the THETA= exponential-option. The default value for
with the THETA= exponential-option. The default value for  is 0. You can specify
is 0. You can specify  with the SIGMA= exponential-option. By default, a maximum likelihood estimate is computed for
with the SIGMA= exponential-option. By default, a maximum likelihood estimate is computed for  . For example, the following statements fit an exponential distribution with
. For example, the following statements fit an exponential distribution with 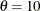 and a maximum likelihood estimate for
and a maximum likelihood estimate for  :
:
proc capability; cdfplot / exponential(theta=10 l=2 color=green); run;
The exponential curve is green and has a line type of 2.
The EXPONENTIAL option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the EXPONENTIAL option.
- GAMMA<(gamma-options)>
-
displays a fitted gamma distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for $x \leq \theta $} \\ \frac{1}{\Gamma (\alpha ) \sigma } \int _{\theta }^ x \left(\frac{t-\theta }{\sigma } \right)^{\alpha - 1} \exp \left( -\frac{t - \theta }{\sigma } \right) dt & \mbox{for $x > \theta $ } \end{array} \right. \]](images/qcug_capability0341.png)
where
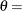 threshold parameter
threshold parameter 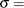 scale parameter
scale parameter 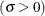
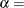 shape parameter
shape parameter 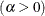
The parameter
 for the gamma distribution must be less than the minimum data value. You can specify
for the gamma distribution must be less than the minimum data value. You can specify  with the THETA= gamma-option. The default value for
with the THETA= gamma-option. The default value for  is 0. In addition, the gamma distribution has a shape parameter
is 0. In addition, the gamma distribution has a shape parameter  and a scale parameter
and a scale parameter  . You can specify these parameters with the ALPHA= and SIGMA= gamma-options. By default, maximum likelihood estimates are computed for
. You can specify these parameters with the ALPHA= and SIGMA= gamma-options. By default, maximum likelihood estimates are computed for  and
and  . For example, the following statements fit a gamma distribution function with
. For example, the following statements fit a gamma distribution function with 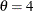 and maximum likelihood estimates for
and maximum likelihood estimates for  and
and  :
:
proc capability; cdfplot / gamma(theta=4); run;
Note that the maximum likelihood estimate of
 is calculated iteratively using the Newton-Raphson approximation. The gamma-options ALPHADELTA=, ALPHAINITIAL=, and MAXITER= control the approximation.
is calculated iteratively using the Newton-Raphson approximation. The gamma-options ALPHADELTA=, ALPHAINITIAL=, and MAXITER= control the approximation.
The GAMMA option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the GAMMA option.
- GUMBEL<(Gumbel-options)>
-
displays a fitted Gumbel distribution (also known as Type 1 extreme value distribution) function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \exp \left( -e^{-(x - \mu )/\sigma } \right) \]](images/qcug_capability0343.png)
where
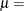 location parameter
location parameter 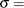 scale parameter
scale parameter 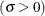
You can specify known values for
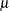 and
and  with the MU= and SIGMA= Gumbel-options. By default, maximum likelihood estimates are computed for
with the MU= and SIGMA= Gumbel-options. By default, maximum likelihood estimates are computed for 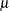 and
and  .
.
The GUMBEL option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the GUMBEL option.
- IGAUSS<(iGauss-options)>
-
displays a fitted inverse Gaussian distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \Phi \left\{ \sqrt {\frac{\lambda }{x}} \left( \frac{x}{\mu } - 1 \right) \right\} + e^{2\lambda /\mu } \Phi \left\{ -\sqrt {\frac{\lambda }{x}} \left( \frac{x}{\mu } + 1 \right) \right\} \]](images/qcug_capability0345.png)
where
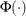 is the standard normal cumulative distribution function, and
is the standard normal cumulative distribution function, and 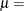 mean parameter
mean parameter 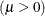
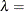 shape parameter
shape parameter 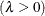
You can specify known values for
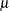 and
and 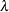 with the MU= and LAMBDA= iGauss-options. By default, maximum likelihood estimates are computed for
with the MU= and LAMBDA= iGauss-options. By default, maximum likelihood estimates are computed for 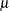 and
and 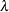 .
.
The IGAUSS option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the IGAUSS option.
- LAMBDA=value
-
specifies the shape parameter
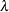 for distribution functions requested with the IGAUSS option. Enclose the LAMBDA= option in parentheses after the IGAUSS distribution keyword. If you do not specify a value for
for distribution functions requested with the IGAUSS option. Enclose the LAMBDA= option in parentheses after the IGAUSS distribution keyword. If you do not specify a value for
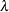 , the procedure calculates a maximum likelihood estimate.
, the procedure calculates a maximum likelihood estimate.
- LEGEND=name | NONE
-
Traditional Graphicsspecifies the name of a LEGEND statement describing the legend for specification limit reference lines and superimposed distribution functions. Specifying LEGEND=NONE, which suppresses all legend information, is equivalent to specifying the NOLEGEND option.
- LOGNORMAL<(lognormal-options)>
-
displays a fitted lognormal distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for $x \leq \theta $} \\ \Phi \left( \frac{\log (x-\theta )-\zeta }{\sigma } \right) & \mbox{for $x > \theta $ } \end{array} \right. \]](images/qcug_capability0350.png)
where
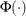 is the standard normal cumulative distribution function, and
is the standard normal cumulative distribution function, and 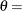 threshold parameter
threshold parameter 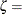 scale parameter
scale parameter 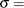 shape parameter
shape parameter 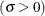
The parameter
 for the lognormal distribution must be less than the minimum data value. You can specify
for the lognormal distribution must be less than the minimum data value. You can specify  with the THETA= lognormal-option. The default value for
with the THETA= lognormal-option. The default value for  is 0. In addition, the lognormal distribution has a shape parameter
is 0. In addition, the lognormal distribution has a shape parameter  and a scale parameter
and a scale parameter 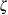 . You can specify these parameters with the SIGMA= and ZETA= lognormal-options. By default, maximum likelihood estimates are computed for
. You can specify these parameters with the SIGMA= and ZETA= lognormal-options. By default, maximum likelihood estimates are computed for  and
and 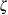 . For example, the following statements fit a lognormal distribution function with
. For example, the following statements fit a lognormal distribution function with 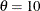 and maximum likelihood estimates for
and maximum likelihood estimates for  and
and 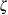 :
:
proc capability; cdfplot / lognormal(theta = 10); run;
The LOGNORMAL option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the LOGNORMAL option.
- MU=value
-
specifies the parameter
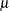 for distribution functions requested with the GUMBEL, IGAUSS, and NORMAL options. Enclose the MU= option in parentheses after the distribution keyword. For the normal and inverse Gaussian distributions,
the default value of
for distribution functions requested with the GUMBEL, IGAUSS, and NORMAL options. Enclose the MU= option in parentheses after the distribution keyword. For the normal and inverse Gaussian distributions,
the default value of 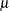 is the sample mean. If you do not specify a value for
is the sample mean. If you do not specify a value for 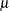 for the Gumbel distribution, the procedure calculates a maximum likelihood estimate.
for the Gumbel distribution, the procedure calculates a maximum likelihood estimate.
- NOCDFLEGEND
-
suppresses the legend for the superimposed theoretical cumulative distribution function.
- NOECDF
-
suppresses the observed distribution function (the empirical cumulative distribution function) of the variable, which is drawn by default. This option enables you to create theoretical cdf plots without displaying the data distribution. The NOECDF option can be used only with a theoretical distribution (such as the NORMAL option).
- NOLEGEND
-
suppresses legends for specification limits, theoretical distribution functions, and hidden observations. Specifying the NOLEGEND option is equivalent to specifying LEGEND=NONE.
- NORMAL<(normal-options)>
-
displays a fitted normal distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left.\begin{array}{ll} \Phi \left( \frac{x - \mu }{\sigma } \right) & \mbox{for $-\infty < x < \infty $} \end{array} \right. \]](images/qcug_capability0353.png)
where
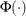 is the standard normal cumulative distribution function, and
is the standard normal cumulative distribution function, and 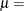 mean
mean 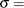 standard deviation
standard deviation 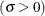
You can specify known values for
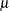 and
and  with the MU= and SIGMA= normal-options, as shown in the following statements:
with the MU= and SIGMA= normal-options, as shown in the following statements:
proc capability; cdfplot / normal(mu=14 sigma=.05); run;
By default, the sample mean and sample standard deviation are calculated for
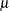 and
and  . The NORMAL option can appear only once in a CDFPLOT statement. For an example, see Output 5.4.1. See Table 5.10 for a list of secondary options you can specify with the NORMAL option.
. The NORMAL option can appear only once in a CDFPLOT statement. For an example, see Output 5.4.1. See Table 5.10 for a list of secondary options you can specify with the NORMAL option.
-
NOSPECLEGEND
NOSPECL -
suppresses the portion of the legend for specification limit reference lines.
- PARETO<(Pareto-options)>
-
displays a fitted generalized Pareto distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = 1 - { \left( 1 - \frac{\alpha (x - \theta )}{\sigma } \right) }^\frac {1}{\alpha } \]](images/qcug_capability0354.png)
where
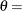 threshold parameter
threshold parameter 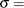 scale parameter
scale parameter 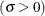
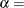 shape parameter
shape parameter
The parameter
 for the generalized Pareto distribution must be less than the minimum data value. You can specify
for the generalized Pareto distribution must be less than the minimum data value. You can specify  with the THETA= Pareto-option. The default value for
with the THETA= Pareto-option. The default value for  is 0. In addition, the generalized Pareto distribution has a shape parameter
is 0. In addition, the generalized Pareto distribution has a shape parameter  and a scale parameter
and a scale parameter  . You can specify these parameters with the ALPHA= and SIGMA= Pareto-options. By default, maximum likelihood estimates are computed for
. You can specify these parameters with the ALPHA= and SIGMA= Pareto-options. By default, maximum likelihood estimates are computed for  and
and  .
.
The PARETO option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the PARETO option.
- POWER<(power-options)>
-
displays a fitted power function distribution on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for $x \leq \theta $} \\ {\left( \frac{x - \theta }{\sigma } \right)}^{\alpha } & \mbox{for $\theta < x < \theta + \sigma $} \\ 1 & \mbox{for $x \geq \theta + \sigma $} \end{array} \right. \]](images/qcug_capability0355.png)
where
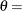 lower threshold parameter (lower endpoint)
lower threshold parameter (lower endpoint) 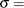 scale parameter
scale parameter 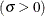
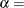 shape parameter
shape parameter 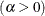
The power function distribution is bounded below by the parameter
 and above by the value
and above by the value 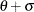 . You can specify
. You can specify  and
and  by using the THETA= and SIGMA= power-options. The default values for
by using the THETA= and SIGMA= power-options. The default values for  and
and  are 0 and 1, respectively.
are 0 and 1, respectively.
You can specify a value for the shape parameter,
 , with the ALPHA= power-option. If you do not specify a value for
, with the ALPHA= power-option. If you do not specify a value for  , the procedure calculates a maximum likelihood estimate.
, the procedure calculates a maximum likelihood estimate.
The power function distribution is a special case of the beta distribution with its second shape parameter,
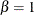 .
.
The POWER option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the POWER option.
- RAYLEIGH<(Rayleigh-options)>
-
displays a fitted Rayleigh distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = 1 - e^{-(x - \theta )^2/(2\sigma ^2)} \]](images/qcug_capability0359.png)
where
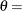 threshold parameter
threshold parameter 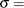 scale parameter
scale parameter 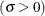
The parameter
 for the Rayleigh distribution must be less than the minimum data value. You can specify
for the Rayleigh distribution must be less than the minimum data value. You can specify  with the THETA= Rayleigh-option. The default value for
with the THETA= Rayleigh-option. The default value for  is 0. You can specify
is 0. You can specify  with the SIGMA= Rayleigh-option. By default, a maximum likelihood estimate is computed for
with the SIGMA= Rayleigh-option. By default, a maximum likelihood estimate is computed for  .
.
The RAYLEIGH option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the RAYLEIGH option.
- SIGMA=value
-
specifies the parameter
 for distribution functions requested by the BETA, EXPONENTIAL, GAMMA, GUMBEL, LOGNORMAL, NORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options. Enclose the SIGMA= option in parentheses after the distribution keyword. The following table summarizes the use
of the SIGMA= option:
for distribution functions requested by the BETA, EXPONENTIAL, GAMMA, GUMBEL, LOGNORMAL, NORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options. Enclose the SIGMA= option in parentheses after the distribution keyword. The following table summarizes the use
of the SIGMA= option:
Distribution Option
SIGMA= Specifies
Default Value
Alias
BETA
scale parameter

1
SCALE=
POWER
EXPONENTIAL
scale parameter

maximum likelihood estimate
SCALE=
GAMMA
WEIBULL
GUMBEL
scale parameter

maximum likelihood estimate
PARETO
RAYLEIGH
LOGNORMAL
shape parameter

maximum likelihood estimate
SHAPE=
NORMAL
scale parameter

standard deviation
- SYMBOL='character'
-
Line Printerspecifies the character used to plot the theoretical distribution function on line printer plots. Enclose the SYMBOL= option in parentheses after the distribution option. The default character is the first letter of the distribution option keyword.
-
THETA=value
THRESHOLD=value -
specifies the lower threshold parameter
 for theoretical cumulative distribution functions requested with the BETA, EXPONENTIAL, GAMMA, LOGNORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options. Enclose the THETA= option in parentheses after the distribution keyword. The default value is 0.
for theoretical cumulative distribution functions requested with the BETA, EXPONENTIAL, GAMMA, LOGNORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options. Enclose the THETA= option in parentheses after the distribution keyword. The default value is 0.
- VSCALE=PERCENT | PROPORTION
-
specifies the scale of the vertical axis. The value PERCENT scales the data in units of percent of observations per data unit. The value PROPORTION scales the data in units of proportion of observations per data unit. The default is PERCENT.
- WEIBULL<(Weibull-options)>
-
displays a fitted Weibull distribution function on the cdf plot. The equation of the fitted cdf is
![\[ F(x) = \left\{ \begin{array}{ll} 0 & \mbox{for $x \leq \theta $} \\ 1 - \exp \left( - \left( \frac{x - \theta }{\sigma } \right)^ c \right) & \mbox{for $x > \theta $ } \end{array} \right. \]](images/qcug_capability0360.png)
where
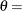 threshold parameter
threshold parameter 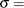 scale parameter
scale parameter 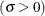
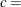 shape parameter
shape parameter 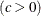
The parameter
 must be less than the minimum data value. You can specify
must be less than the minimum data value. You can specify  with the THETA= Weibull-option. The default value for
with the THETA= Weibull-option. The default value for  is 0. In addition, the Weibull distribution has a shape parameter c and a scale parameter
is 0. In addition, the Weibull distribution has a shape parameter c and a scale parameter  . You can specify these parameters with the SIGMA= and C= Weibull-options. By default, maximum likelihood estimates are computed for c and
. You can specify these parameters with the SIGMA= and C= Weibull-options. By default, maximum likelihood estimates are computed for c and  . For example, the following statements fit a Weibull distribution function with
. For example, the following statements fit a Weibull distribution function with 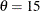 and maximum likelihood estimates for
and maximum likelihood estimates for  and c:
and c:
proc capability; cdfplot / weibull(theta=15); run;
Note that the maximum likelihood estimate of c is calculated iteratively using the Newton-Raphson approximation. The Weibull-options CDELTA=, CINITIAL=, and MAXITER= control the approximation.
The WEIBULL option can appear only once in a CDFPLOT statement. See Table 5.10 for a list of secondary options you can specify with the WEIBULL option.
- ZETA=value
-
specifies a value for the scale parameter
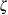 for a lognormal distribution function requested with the LOGNORMAL option. Enclose the ZETA= option in parentheses after
the LOGNORMAL keyword. If you do not specify a value for
for a lognormal distribution function requested with the LOGNORMAL option. Enclose the ZETA= option in parentheses after
the LOGNORMAL keyword. If you do not specify a value for 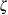 , a maximum likelihood estimate is computed. You can specify the SCALE= option as an alias for the ZETA= option.
, a maximum likelihood estimate is computed. You can specify the SCALE= option as an alias for the ZETA= option.
