XCHART Statement: SHEWHART Procedure
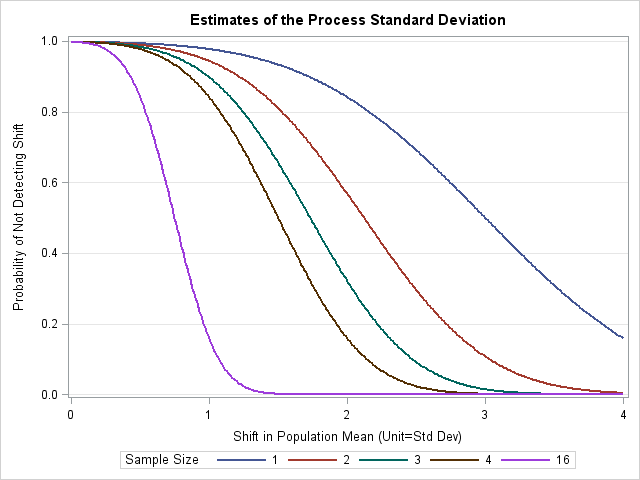
Example 17.36 Plotting OC Curves for Mean Charts
See SHWOC1 in the SAS/QC Sample LibraryThis example uses the GPLOT procedure and the DATA step function PROBNORM to plot operating characteristic (OC) curves for
![]() charts with 3
charts with 3![]() limits. An OC curve is plotted for each of the subgroup samples sizes 1, 2, 3, 4, and 16. Refer to page 226 in Montgomery
(1996). Each curve plots the probability
limits. An OC curve is plotted for each of the subgroup samples sizes 1, 2, 3, 4, and 16. Refer to page 226 in Montgomery
(1996). Each curve plots the probability ![]() of not detecting a shift of magnitude
of not detecting a shift of magnitude ![]() in the process mean as a function of
in the process mean as a function of ![]() . The value of
. The value of ![]() is computed using the following formula:
is computed using the following formula:
|
|
|
|
|
|
|
|
The following statements compute ![]() (the variable BETA) as a function of
(the variable BETA) as a function of ![]() (the variable NU). The variable
(the variable NU). The variable nSample contains the sample size.
data oc;
keep prob nSample t plot2;
plot2=.;
do nSample=1, 2, 3, 4, 16;
do j=0 to 400;
t=j/100;
prob=probnorm( 3-t*sqrt(nSample)) -
probnorm(-3-t*sqrt(nSample));
output;
end;
end;
label t ='Shift in Population Mean (Unit=Std Dev)'
prob='Probability of Not Detecting Shift';
run;
The following statements use the GPLOT procedure to display the OC curves shown in Output 17.36.1:
proc sgplot data=oc;
series x=t y=prob /
group=nSample lineattrs=(pattern=solid thickness=2);
yaxis grid;
label nSample='Sample Size';
run;
Output 17.36.1: OC Curves for Different Subgroup Sample Sizes