IRCHART Statement: SHEWHART Procedure

Constructing Charts for Individual Measurements and Moving Ranges

The following notation is used in this section:

$\mu$

process mean (expected value of the population of measurements)

$\sigma$

process standard deviation (standard deviation of the population of measurements)

$X_{i}$

the ith individual measurement

$\bar{X}$

mean of the individual measurements, computed as $(X_1+\cdots +X_ N)/N$ , where N is the number of individual measurements

number of consecutive measurements used to calculate the moving ranges (by default, n = 2)

$R_{i}$

moving range computed for the ith subgroup (corresponding to the ith individual measurement). If , then is assigned a missing value. Otherwise,

$R_ i = \max (X_ i,X_{i-1},\ldots ,X_{i-n+1}) - \min (X_ i,X_{i-1},\ldots ,X_{i-n+1})$

This formula assumes that $X_ i, X_{i-1},\ldots ,X_{i-n+1}$ are nonmissing.

$\bar{R}$

average of the nonmissing moving ranges, computed as

$\frac{R_ n + R_{n+1} \cdots + R_ N}{N+1-n}$

$d_{2}(n)$

expected value of the range of n independent normally distributed variables with unit standard deviation

$d_{3}(n)$

standard error of the range of n independent observations from a normal population with unit standard deviation

$z_{p}$

100pth percentile (0 < p < 1) of the standard normal distribution

$D_{p}(n)$

100pth percentile (0 < p < 1) of the distribution of the range of n independent observations from a normal population with unit standard deviation

Plotted Points

Each point on an individual measurements chart, indicates the value of a measurement ().

Each point on a moving range chart indicates the value of a moving range ( $R_{i}$ ). With n = 2, for example, if the first three measurements are 3.4, 3.7, and 3.6, the first moving range is missing, the second moving range is , and the third moving range is .

Central Lines

By default, the central line on an individual measurements chart indicates an estimate for $\mu$ , which is computed as $\bar{X}$ . If you specify a known value ( $\mu _{0}$ ) for $\mu$ , the central line indicates the value of $\mu _{0}$ .

The central line on a moving range chart indicates an estimate for the expected moving range, computed as $d_{2}(n)\hat{\sigma }$ where $\hat{\sigma } = \bar{R}/d_2(n)$ . If you specify a known value ( $\hat{\sigma }_0$ ) for $\sigma$ , the central line indicates the value of $d_{2}(n)\sigma _{0}$ .

Control Limits

You can compute the limits

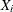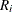as a specified multiple (k) of the standard errors of $X_{i}$ and $R_{i}$ above and below the central line. The default limits are computed with k = 3 (these are referred to as 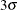$3\sigma$ limits).
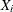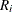as probability limits defined in terms of $\alpha$ , a specified probability that $X_{i}$ or $R_{i}$ exceeds the limits

The following table provides the formulas for the limits:

Table 17.20: Limits for Individual Measurements and Moving Range Charts

Control Limits
Individual Measurements Chart	LCL = lower control limit = $\bar{X} - k\hat{\sigma }$
	UCL = upper control limit = $\bar{X} + k\hat{\sigma }$
Moving Range Chart	LCL = lower control limit = $\max (d_{2}(n)\hat{\sigma } - kd_{3}(n)\hat{\sigma },0)$
	UCL = upper control limit = $d_{2}(n)\hat{\sigma } + kd_{3}(n)\hat{\sigma }$

Probability Limits
Individual Measurements Chart	LCL = lower control limit = $\bar{X} - z_{\alpha /2}\hat{\sigma }$
	UCL = upper control limit = $\bar{X} + z_{\alpha /2}\hat{\sigma }$
Moving Range Chart	LCL = lower control limit = $D_{\alpha /2}(n)\hat{\sigma }$
	UCL = upper control limit = $D_{1-\alpha /2}(n)\hat{\sigma }$

The formulas assume that the measurements are normally distributed. Note that the probability limits for the moving range are asymmetric about the central line. If standard values $\mu _{0}$ and $\sigma _{0}$ are available for $\mu$ and $\sigma$ , replace $\bar{X}$ with $\mu _{0}$ and $\hat{\sigma }$ with $\sigma _{0}$ in Table 17.20.

You can specify parameters for the limits as follows:

Specify k with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
Specify $\alpha$ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
Specify n with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
Specify 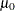$\mu _{0}$ with the MU0= option or with the variable _MEAN_ in the LIMITS= data set.
Specify 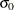$\sigma _{0}$ with the SIGMA0= option or with the variable _STDDEV_ in the LIMITS= data set.