The UNIVARIATE Procedure

Modeling a Data Distribution

In addition to summarizing a data distribution as in the preceding example, you can use PROC UNIVARIATE to statistically model a distribution based on a random sample of data. The following statements create a data set named Aircraft that contains the measurements of a position deviation for a sample of 30 aircraft components. 

data Aircraft;
   input Deviation @@;
   label Deviation = 'Position Deviation';
   datalines;
-.00653 0.00141 -.00702 -.00734 -.00649 -.00601
-.00631 -.00148 -.00731 -.00764 -.00275 -.00497
-.00741 -.00673 -.00573 -.00629 -.00671 -.00246
-.00222 -.00807 -.00621 -.00785 -.00544 -.00511
-.00138 -.00609 0.00038 -.00758 -.00731 -.00455
;

An initial question in the analysis is whether the measurement distribution is normal. The following statements request a table of moments, the tests for normality, and a normal probability plot, which are shown in Figure 4.5 and Figure 4.6: 

title 'Position Deviation Analysis';
ods graphics on;
ods select Moments TestsForNormality ProbPlot;
proc univariate data=Aircraft normaltest;
   var Deviation;
   probplot Deviation / normal(mu=est sigma=est)
                        square
                        odstitle = title;
   label Deviation = 'Position Deviation';
   inset  mean std / format=6.4;
run;

PROC UNIVARIATE uses the label associated with the variable Deviation as the vertical axis label in the probability plot. The INSET statement displays the sample mean and standard deviation on the probability plot.

Figure 4.5: Moments and Tests for Normality

Position Deviation Analysis

The UNIVARIATE Procedure
Variable: Deviation (Position Deviation)

Moments
N 30 Sum Weights 30
Mean -0.0053067 Sum Observations -0.1592
Std Deviation 0.00254362 Variance 6.47002E-6
Skewness 1.2562507 Kurtosis 0.69790426
Uncorrected SS 0.00103245 Corrected SS 0.00018763
Coeff Variation -47.932613 Std Error Mean 0.0004644

Tests for Normality
Test Statistic p Value
Shapiro-Wilk W 0.845364 Pr < W 0.0005
Kolmogorov-Smirnov D 0.208921 Pr > D <0.0100
Cramer-von Mises W-Sq 0.329274 Pr > W-Sq <0.0050
Anderson-Darling A-Sq 1.784881 Pr > A-Sq <0.0050


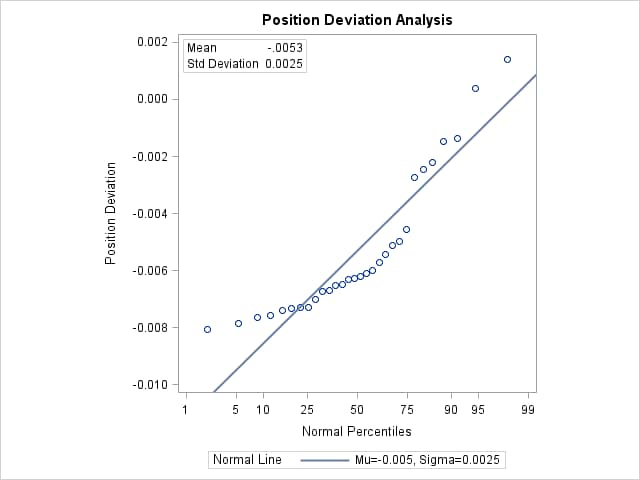
All four goodness-of-fit tests in Figure 4.5 reject the hypothesis that the measurements are normally distributed.

Figure 4.6 shows a normal probability plot for the measurements. A linear pattern of points following the diagonal reference line would indicate that the measurements are normally distributed. Instead, the curved point pattern suggests that a skewed distribution, such as the lognormal, is more appropriate than the normal distribution.

A lognormal distribution for Deviation is fitted in Example 4.26.

A sample program for this example, univar2.sas, is available in the SAS Sample Library for Base SAS software.

Figure 4.6: Normal Probability Plot

Normal Probability Plot