The CORR Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Pearson Product-Moment CorrelationSpearman Rank-Order CorrelationKendall’s Tau-b Correlation CoefficientHoeffding Dependence CoefficientPartial CorrelationFisher’s z TransformationPolychoric CorrelationPolyserial CorrelationCronbach’s Coefficient AlphaConfidence and Prediction EllipsesMissing ValuesIn-Database ComputationOutput TablesOutput Data SetsODS Table NamesODS Graphics
Pearson Product-Moment CorrelationSpearman Rank-Order CorrelationKendall’s Tau-b Correlation CoefficientHoeffding Dependence CoefficientPartial CorrelationFisher’s z TransformationPolychoric CorrelationPolyserial CorrelationCronbach’s Coefficient AlphaConfidence and Prediction EllipsesMissing ValuesIn-Database ComputationOutput TablesOutput Data SetsODS Table NamesODS Graphics -
Examples
 Computing Four Measures of AssociationComputing Correlations between Two Sets of VariablesAnalysis Using Fisher’s z TransformationApplications of Fisher’s z TransformationComputing Polyserial CorrelationsComputing Cronbach’s Coefficient AlphaSaving Correlations in an Output Data SetCreating Scatter PlotsComputing Partial Correlations
Computing Four Measures of AssociationComputing Correlations between Two Sets of VariablesAnalysis Using Fisher’s z TransformationApplications of Fisher’s z TransformationComputing Polyserial CorrelationsComputing Cronbach’s Coefficient AlphaSaving Correlations in an Output Data SetCreating Scatter PlotsComputing Partial Correlations - References
Example 2.8 Creating Scatter Plots
The following statements request a correlation analysis and a scatter plot matrix for the variables in the data set Fish1, which was created in Example 2.6.
ods graphics on; title 'Fish Measurement Data'; proc corr data=fish1 nomiss plots=matrix(histogram); var Height Width Length3 Weight3; run;
The "Simple Statistics" table in Output 2.8.1 displays univariate descriptive statistics for analysis variables.
Output 2.8.1: Simple Statistics
The "Pearson Correlation Coefficients" table in Output 2.8.2 displays Pearson correlation statistics for pairs of analysis variables.
Output 2.8.2: Pearson Correlation Coefficients
| Pearson Correlation Coefficients, N = 34 Prob > |r| under H0: Rho=0 |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Height | Width | Length3 | Weight3 | |||||||||
| Height |
|
|
|
|
||||||||
| Width |
|
|
|
|
||||||||
| Length3 |
|
|
|
|
||||||||
| Weight3 |
|
|
|
|
||||||||
The variables are highly correlated. For example, the correlation between Height and Width is 0.92632.
The PLOTS=MATRIX(HISTOGRAM) option requests a scatter plot matrix for the VAR statement variables in Output 2.8.3.
Output 2.8.3: Scatter Plot Matrix
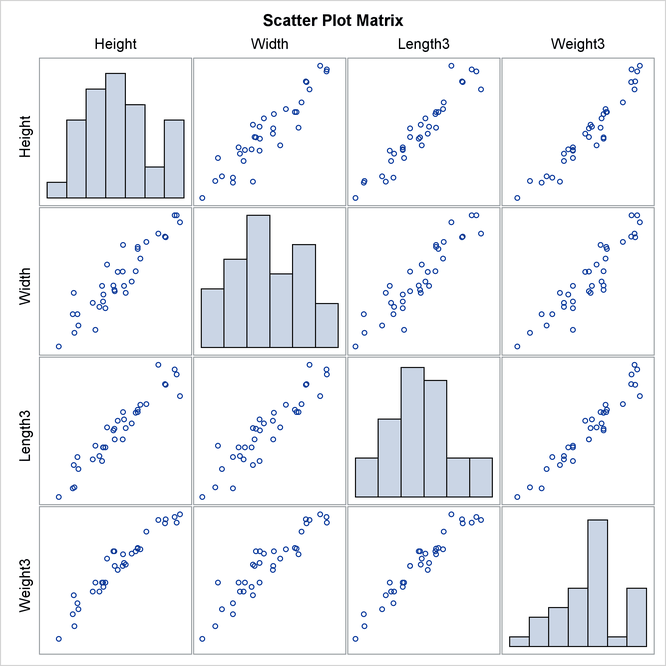
Note that this graphical display is requested by enabling ODS Graphics and by specifying the PLOTS= option. For more information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS in SAS/STAT 14.1 User's Guide.
To explore the correlation between Height and Width, the following statements display (in Output 2.8.4) a scatter plot with prediction ellipses for the two variables:
ods graphics on;
proc corr data=fish1 nomiss
plots=scatter(nvar=2 alpha=.20 .30);
var Height Width Length3 Weight3;
run;
The PLOTS=SCATTER(NVAR=2) option requests a scatter plot for the first two variables in the VAR list. The ALPHA=.20 .30 suboption
requests 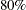 and
and 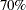 prediction ellipses, respectively.
prediction ellipses, respectively.
Output 2.8.4: Scatter Plot with Prediction Ellipses
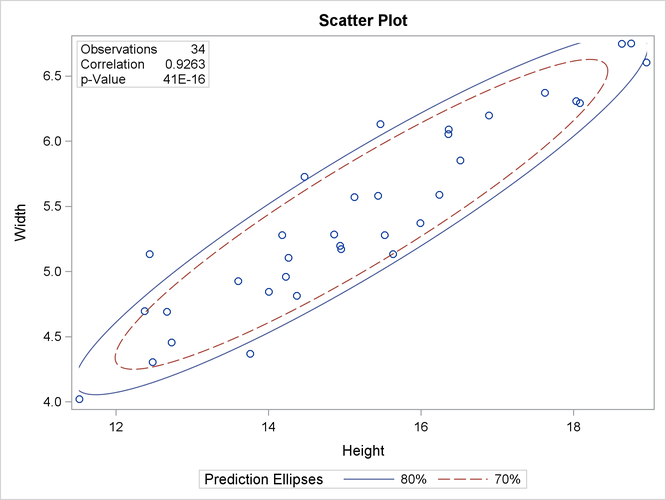
A prediction ellipse is a region for predicting a new observation from the population, assuming bivariate normality. It also
approximates a region that contains a specified percentage of the population. The displayed prediction ellipse is centered
at the means 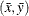 . For further details, see the section Confidence and Prediction Ellipses.
. For further details, see the section Confidence and Prediction Ellipses.
Note that the following statements also display (in Output 2.8.5) a scatter plot for Height and Width:
ods graphics on;
proc corr data=fish1
plots=scatter(alpha=.20 .30);
var Height Width;
run;
Output 2.8.5: Scatter Plot with Prediction Ellipses
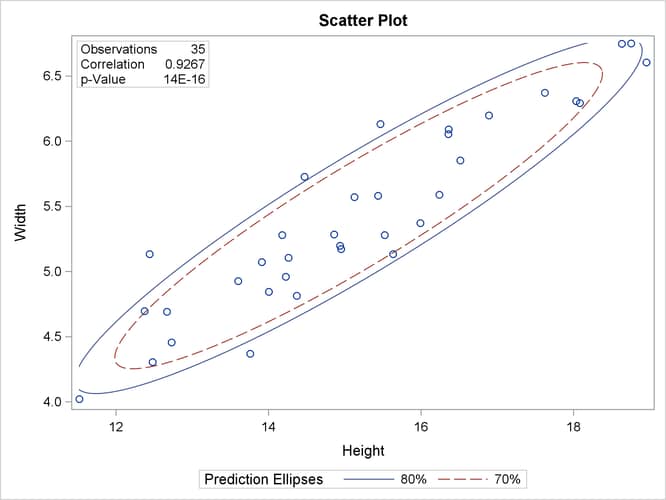
Output 2.8.5 includes the point 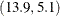 , which was excluded from Output 2.8.4 because the observation had a missing value for
, which was excluded from Output 2.8.4 because the observation had a missing value for Weight3. The prediction ellipses in Output 2.8.5 also reflect the inclusion of this observation.
The following statements display (in Output 2.8.6) a scatter plot with confidence ellipses for the mean:
ods graphics on;
title 'Fish Measurement Data';
proc corr data=fish1 nomiss
plots=scatter(ellipse=confidence nvar=2 alpha=.05 .01);
var Height Width Length3 Weight3;
run;
The NVAR=2 suboption within the PLOTS= option restricts the number of plots created to the first two variables in the VAR
statement, and the ELLIPSE=CONFIDENCE suboption requests confidence ellipses for the mean. The ALPHA=.05 .01 suboption requests
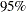 and
and 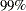 confidence ellipses, respectively.
confidence ellipses, respectively.
Output 2.8.6: Scatter Plot with Confidence Ellipses
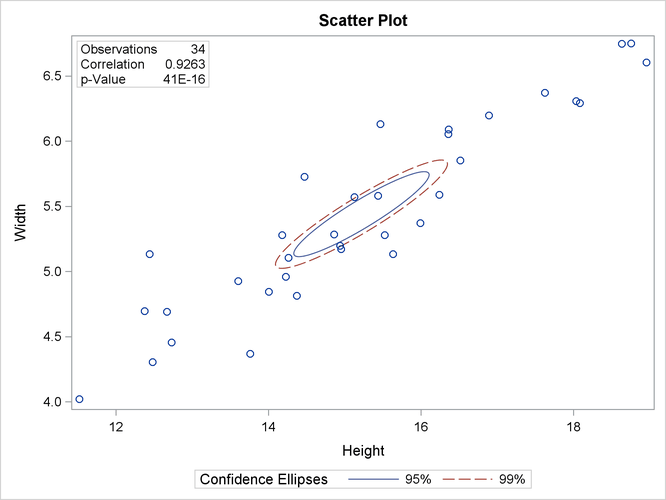
The confidence ellipse for the mean is centered at the means 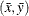 . For further details, see the section Confidence and Prediction Ellipses.
. For further details, see the section Confidence and Prediction Ellipses.