The CORR Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Pearson Product-Moment CorrelationSpearman Rank-Order CorrelationKendall’s Tau-b Correlation CoefficientHoeffding Dependence CoefficientPartial CorrelationFisher’s z TransformationPolychoric CorrelationPolyserial CorrelationCronbach’s Coefficient AlphaConfidence and Prediction EllipsesMissing ValuesIn-Database ComputationOutput TablesOutput Data SetsODS Table NamesODS Graphics
Pearson Product-Moment CorrelationSpearman Rank-Order CorrelationKendall’s Tau-b Correlation CoefficientHoeffding Dependence CoefficientPartial CorrelationFisher’s z TransformationPolychoric CorrelationPolyserial CorrelationCronbach’s Coefficient AlphaConfidence and Prediction EllipsesMissing ValuesIn-Database ComputationOutput TablesOutput Data SetsODS Table NamesODS Graphics -
Examples
 Computing Four Measures of AssociationComputing Correlations between Two Sets of VariablesAnalysis Using Fisher’s z TransformationApplications of Fisher’s z TransformationComputing Polyserial CorrelationsComputing Cronbach’s Coefficient AlphaSaving Correlations in an Output Data SetCreating Scatter PlotsComputing Partial Correlations
Computing Four Measures of AssociationComputing Correlations between Two Sets of VariablesAnalysis Using Fisher’s z TransformationApplications of Fisher’s z TransformationComputing Polyserial CorrelationsComputing Cronbach’s Coefficient AlphaSaving Correlations in an Output Data SetCreating Scatter PlotsComputing Partial Correlations - References
Cronbach’s Coefficient Alpha
Analyzing latent constructs such as job satisfaction, motor ability, sensory recognition, or customer satisfaction requires instruments to accurately measure the constructs. Interrelated items can be summed to obtain an overall score for each participant. Cronbach’s coefficient alpha estimates the reliability of this type of scale by determining the internal consistency of the test or the average correlation of items within the test (Cronbach 1951).
When a value is recorded, the observed value contains some degree of measurement error. Two sets of measurements on the same variable for the same individual might not have identical values. However, repeated measurements for a series of individuals will show some consistency. Reliability measures internal consistency from one set of measurements to another. The observed value Y is divided into two components, a true value T and a measurement error E. The measurement error is assumed to be independent of the true value; that is,
![\[ Y=T+E \, \, \, \, \, \, \, \, \mr{Cov}(T,E)=0 \]](images/procstat_corr0187.png)
The reliability coefficient of a measurement test is defined as the squared correlation between the observed value Y and the true value T; that is,
![\[ r^{2}(Y,T)=\frac{\mr{Cov}(Y,T)^2}{\mr{V}(Y) \mr{V}(T)} =\frac{\mr{V}(T)^2}{\mr{V}(Y) \mr{V}(T)} =\frac{\mr{V}(T)}{\mr{V}(Y)} \]](images/procstat_corr0188.png)
which is the proportion of the observed variance due to true differences among individuals in the sample. If Y is the sum of several observed variables measuring the same feature, you can estimate 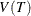 . Cronbach’s coefficient alpha, based on a lower bound for
. Cronbach’s coefficient alpha, based on a lower bound for 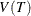 , is an estimate of the reliability coefficient.
, is an estimate of the reliability coefficient.
Suppose p variables are used with 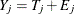 for
for 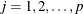 , where
, where 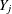 is the observed value,
is the observed value, 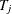 is the true value, and
is the true value, and 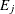 is the measurement error. The measurement errors (
is the measurement error. The measurement errors (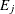 ) are independent of the true values (
) are independent of the true values (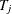 ) and are also independent of each other. Let
) and are also independent of each other. Let 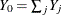 be the total observed score and let
be the total observed score and let 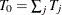 be the total true score. Because
be the total true score. Because
![\[ (p-1) \sum _{j} V(T_ j) \geq \sum _{i \neq j} \mr{Cov}(T_ i,T_ j) \]](images/procstat_corr0197.png)
a lower bound for 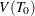 is given by
is given by
![\[ \frac{p}{p-1} \sum _{i \neq j} \mr{Cov}(T_ i,T_ j) \]](images/procstat_corr0199.png)
With 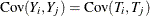 for
for 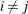 , a lower bound for the reliability coefficient,
, a lower bound for the reliability coefficient, 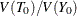 , is then given by the Cronbach’s coefficient alpha:
, is then given by the Cronbach’s coefficient alpha:
![\[ \alpha = \left(\frac{p}{p-1}\right)\frac{\sum _{i \neq j} \mr{Cov}(Y_ i,Y_ j)}{V(Y_0)} = \left(\frac{p}{p-1}\right)\left(1-\frac{\sum _{j}V(Y_ j)}{V(Y_0)}\right) \]](images/procstat_corr0203.png)
If the variances of the items vary widely, you can standardize the items to a standard deviation of 1 before computing the coefficient alpha. If the variables are dichotomous (0,1), the coefficient alpha is equivalent to the Kuder-Richardson 20 (KR-20) reliability measure.
When the correlation between each pair of variables is 1, the coefficient alpha has a maximum value of 1. With negative correlations between some variables, the coefficient alpha can have a value less than zero. The larger the overall alpha coefficient, the more likely that items contribute to a reliable scale. Nunnally and Bernstein (1994) suggests 0.70 as an acceptable reliability coefficient; smaller reliability coefficients are seen as inadequate. However, this varies by discipline.
To determine how each item reflects the reliability of the scale, you calculate a coefficient alpha after deleting each variable independently from the scale. Cronbach’s coefficient alpha from all variables except the kth variable is given by
![\[ \alpha _ k=\left(\frac{p-1}{p-2}\right) \left( 1-\frac{\sum _{i\neq k} V(Y_ i)}{V(\sum _{i\neq k}Y_ i)} \right) \]](images/procstat_corr0204.png)
If the reliability coefficient increases after an item is deleted from the scale, you can assume that the item is not correlated highly with other items in the scale. Conversely, if the reliability coefficient decreases, you can assume that the item is highly correlated with other items in the scale. Refer to Yu (2001) for more information about how to interpret Cronbach’s coefficient alpha.
Listwise deletion of observations with missing values is necessary to correctly calculate Cronbach’s coefficient alpha. PROC CORR does not automatically use listwise deletion if you specify the ALPHA option. Therefore, you should use the NOMISS option if the data set contains missing values. Otherwise, PROC CORR prints a warning message indicating the need to use the NOMISS option with the ALPHA option.